Пример вычисления определенного интеграла методом трапеций

Вычислить приближенно определенный интеграл по формуле трапеций с точностью до двух знаков после запятой (до 0,01).
.

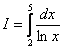Решение:Мы не знаем, НА СКОЛЬКО отрезков разбивать отрезок интегрирования, чтобы получить два верных знака после запятой. Иными словами, мы не знаем значение .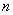

Существует специальная формула, позволяющая определить количество отрезков разбиения, чтобы гарантированно достигнуть требуемой точности, но практике она часто трудноприменима. Поэтому выгодно использовать упрощенный подход.

Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 2-3-4-5. Разобьем отрезок интегрирования, например, на 5 частей:

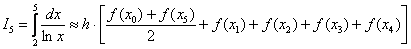
Шаг тоже известен: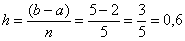

Тут возникает еще один вопрос, до какого разряда округлять результаты 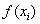? Общая рекомендация такова:к требуемой точности нужно прибавить 2-3 разряда. В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):

В результате:

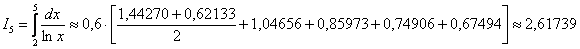
После первичного результата количество отрезков удваивают. В данном случае необходимо провести разбиение на 10 отрезков.

Для 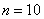формула трапеций приобретает следующий вид:

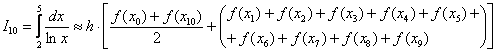
Вычислим шаг разбиения: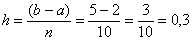

Результаты расчётов сведём в таблицу:

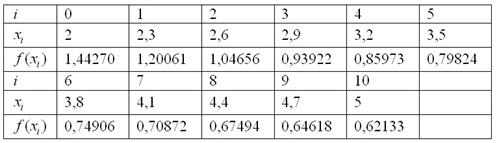
В результате:

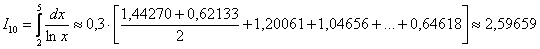
Теперь рассчитаем, на сколько улучшился результат:

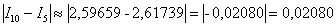
Здесь используем знак модуля, поскольку нас интересует абсолютная разность.

Полученная оценка погрешности больше, чем требуемая точность:

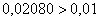
Поэтому необходимо ещё раз удвоить количество отрезков разбиения до 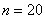, и вычислить уже :

.

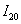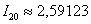Снова оцениваем погрешность:

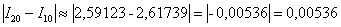
Полученная оценка погрешности меньше, чем требуемая точность:

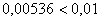
Всё что осталось сделать, округлить последний (наиболее точный) результат 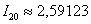до двух знаков после запятой и записать:

Ответ: 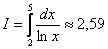с точностью до 0,01

Пример решения задачи 2.5 для одного интеграла см. в приложении 2.

Желательно проверить результаты расчетов значений определенных интегралов в математическом пакете Mathcad.

Приложение 1

Образец титульного листа

Приложение 1

Пример выполнения задания №2

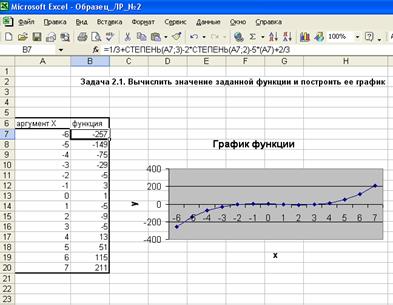
Задача 2.1

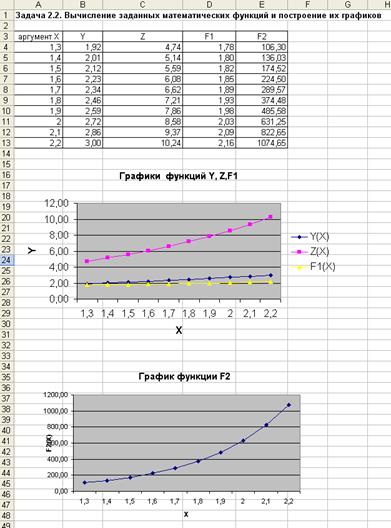
Задача 2.2

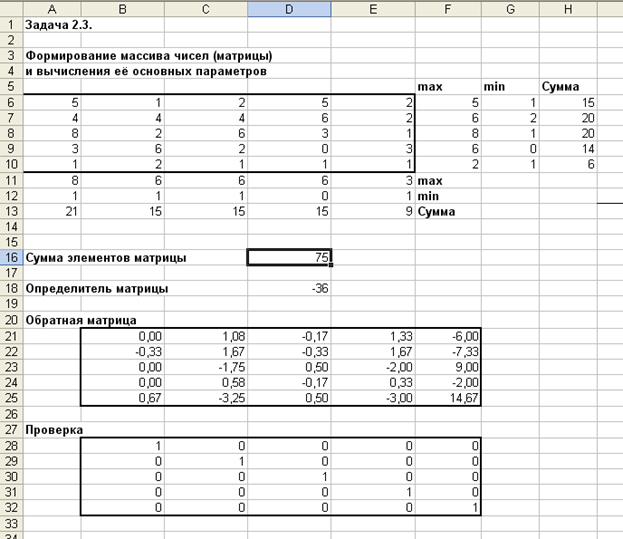
Задача 2.3

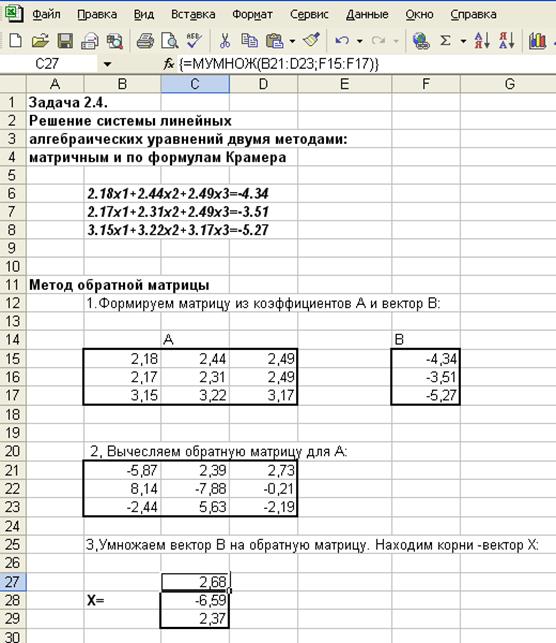
Задача 2.4

Задача 2.5. (для одного интеграла)

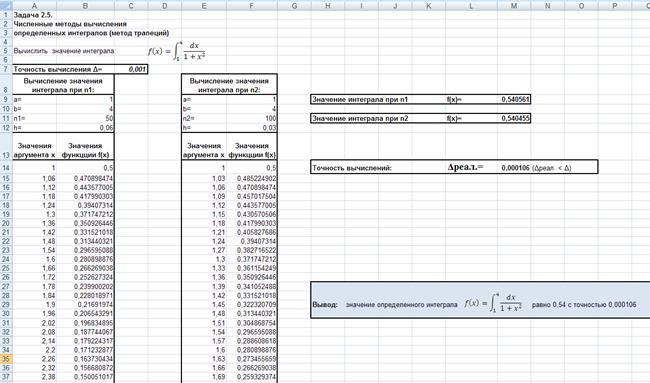
Проверка результатов расчетов в Mathcad:

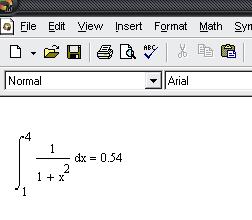
Формулы к задачам

Задача 2.1.

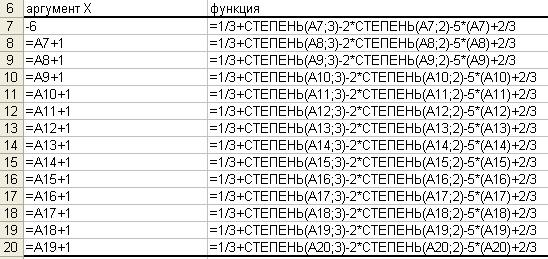
Задача 2.2.

Задача 2.3.

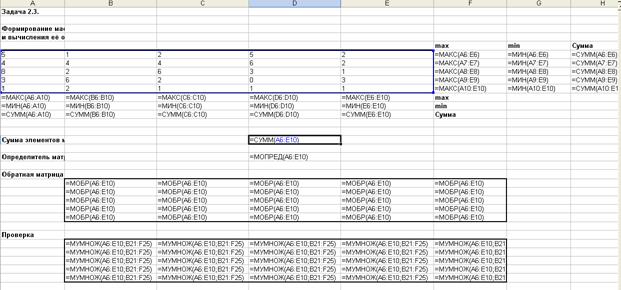
Задача 2.4.

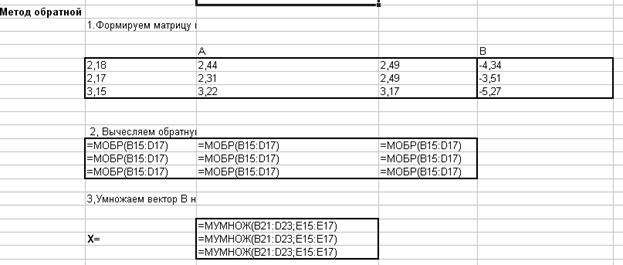
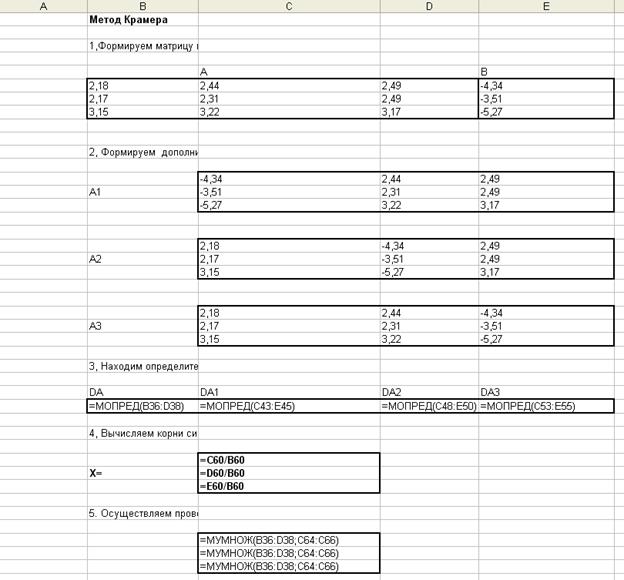
Задача 2.5.

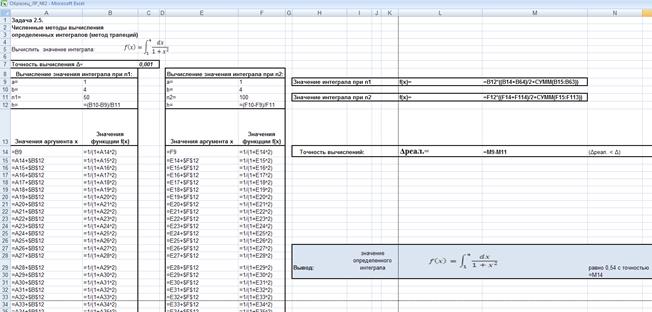
Аналогично выполнить расчет для второго интеграла согласно варианту задания.

Примечание: при расчете значений аргумента x используется абсолютная ссылка на ячейки. Обозначается абсолютная ссылка с помощью символа “$” на строку или столбец, или на строку и столбец одновременно, например, $B$12).

Абсолютная ссылка дает возможность ссылаться на одну и ту же ячейку при копировании формулы (в отличие от относительной ссылки). Таким образом, мы можем в первой строке сослаться на конкретную ячейку, скопировать ее и протянуть до конца списка. Весь список будет ссылаться на ту ячейку, в которой действует абсолютная ссылка. Соответственно при изменении этой ячейки меняется весь столбец или строка.