Классический метод анализа переходных колебаний в ЭЦ

Пример П1.1

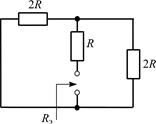
В цепи, схема которой представлена на рис. П1.1, в момент времени t = 0 замыкается ключ. Найдите законы изменения тока i_L(t) и напряжения u_L(t) для t ³ 0, если до коммутации в цепи был режим постоянного тока.

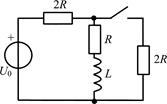Рис. П1.1	Рис. П1.2

Решение

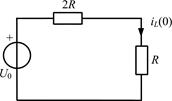
Найдем начальные условия задачи. В данном случае это ток через индуктивность при t = 0. Закон коммутации позволяет найти этот ток в момент t = 0_–, когда ключ был еще разомкнут, и в цепи имел место режим постоянного тока, при котором напряжение на зажимах индуктивности равно нулю, что эквивалентно короткому замыканию ее зажимов (рис. П1.2):

.

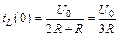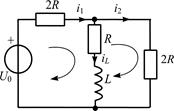Рис. П1.3

Составим систему уравнений по законам Кирхгофа для цепи после коммутации (рис. П1.3):

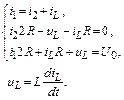
Преобразуем составленную сис­тему уравнений методом подстановок в одно дифференциальное уравнение с переменной i_L, для которой выполняется закон коммутации.

Для этого выразим все токи через i_L и подставим в уравнение, содержащее задающее напряжение источника:

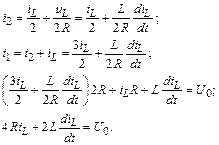
Полученное дифференциальное уравнение удобно привести к виду

,

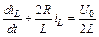где коэффициент переменной i_L – 2R/L = 1/t, что позволяет проверить правильность составления этого уравнения, определив постоянную времени цепи t = L/R_э по схеме.

Решение неоднородного дифференциального уравнения запишем в виде суммы свободной и вынужденной составляющих:

i_L(t) = i_{L вын} + i_{L св} = i_{L вын} + Ae^pt.

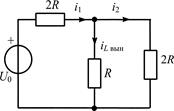Рис. П1.4

Вынужденную составляющую решения i_{L вын} найдем при t ® ¥, когда цепь будет в режиме постоянного тока (рис. П1.4):

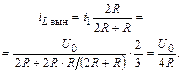
Постоянную интегрирования A найдем из закона коммутации по известным начальным условиям задачи:

при t = 0 i_L(0_–) = i_L(0₊),

i_L(0_–) = i_{L вын} + A,

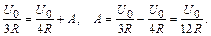
Характеристическое уравнение цепи p + 2R/L = 0 имеет корень p = –2R/L, постоянная времени цепи t = –1/p = L/2R.

Таким образом, ток через индуктивность после коммутации изменяется по закону

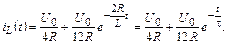
Тогда

.

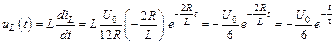Аналогичный результат можно получить, используя общую формулу, в которой для рассматриваемого примера

f(0) = i_L(0) = U₀/3R; f(¥) = i_{L вын} = U₀/4R; t = L/R_э = L/2R,

Рис. П1.5

где R_э рассчитано относительно зажимов индуктивности при условии, что U₀ = 0 (рис. П1.5):

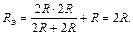
На рис. П1.6 представлены примерные графики зависимостей тока и напряжения на индуктивности от времени.

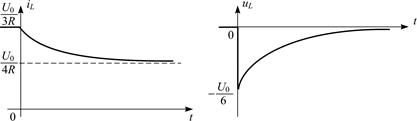
Рис. П1.6

Пример П1.2

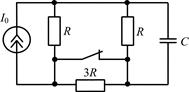Рис. П1.7

В цепи, схема которой представлена на рис. П1.7, в момент времени t = 0 ключ размыкается. Найдите законы изменения напряжения u_C(t) и тока i_C(t) для t ³ 0, если до коммутации в цепи был режим постоянного тока.

Решение

Найдем начальные условия задачи, в данном случае – значение u_C(0). До коммутации (t < 0), когда ключ был замкнут, и в цепи был режим постоянного тока, ток через емкость был равен нулю, что эквивалентно размыканию ветви с емкостью (рис. П1.8), тогда

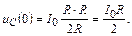
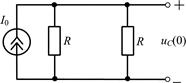Рис. П1.8

Рис. П1.9

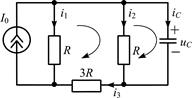
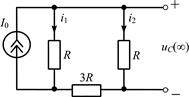
Составим систему уравнений по законам Кирхгофа для цепи после коммутации (рис. П1.9):

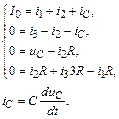
Преобразуем составленную систему уравнений методом подстановок в одно дифференциальное уравнение с переменной u_C, для которой выполняется закон коммутации.

Для этого выразим все токи через u_C и подставим в уравнение, содержащее ток источника:

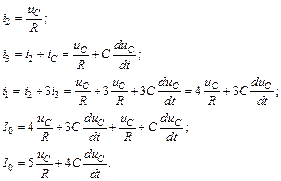
Полученное дифференциальное уравнение удобно привести к виду

,

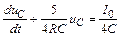где коэффициент переменной u_C – 5/4RC = 1/t, что позволяет проверить правильность составления этого уравнения, определив постоянную времени цепи t = R_эC по схеме.

Решение неоднородного дифференциального уравнения запишем как сумму свободной и вынужденной составляющих:

u_C(t) = u_{C вын} + u_{C св} = u_{C вын} + Ae^pt.

Рис. П1.10

Вынужденную составляющую решения найдем при t ® ¥, когда в цепи будет режим постоянного тока (рис. П1.10):

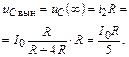
Постоянную интегрирования A найдем из закона коммутации по известным начальным условиям задачи:

при t = 0, u_C(0_–) = u_C(0₊),

u_C(0_–) = u_{C вын} + A,

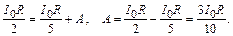
Характеристическое уравнение цепи p + 5/4RC = 0 имеет корень p = –5/4RC, постоянная времени цепи t = –1/p = 4RC/5 = 0,8RC.

Таким образом, напряжение на емкости после коммутации изменяется по закону

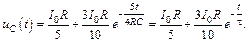
Тогда

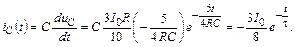
Аналогичный результат можно получить, используя общую формулу, в которой для рассматриваемого примера

f(0) = u_C(0) = I₀ R/2; f(¥) = u_{C вын} = I₀R/5; t = R_эC = 4RC/5,

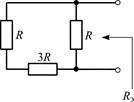Рис. П1.11

где R_э рассчитано относительно зажимов емкости при условии, что I₀ = 0 (рис. П1.11):

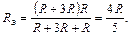
На рис. П1.12 представлены примерные графики зависимостей напряжения и тока на емкости от времени.

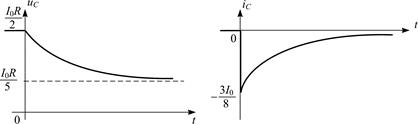
Рис. П1.12

Пример П1.3

Рис. П1.13

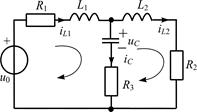
Составьте систему линейных дифференциальных уравнений по методу переменных состояния в нормальной форме для цепи на рис. П1.13, используя законы Кирхгофа. Запишите полученную систему уравнений состояния в матричной форме.

Решение

Переменными состояния, определяющими общий запас энергии цепи на рис. П1.13, являются: напряжение на емкости u_C, токи в индуктивностях i_L1 и i_L2. Порядок системы линейных дифференциальных уравнений по методу переменных состояния для данной цепи равен числу реактивных элементов, а значит – 3.

Составим систему уравнений по законам Кирхгофа с учетом выбранных положительных направлений переменных состояния u_C, i_L1, i_L2 и обхода контуров на рис. П1.13:

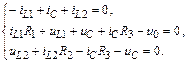
Преобразуем полученную систему уравнений, если известно:

i_C = i_L1 – i_L2; i_C = Сu_C /dt; u_L1 = L₁di_L1/dt; u_L2 = L₂di_L2/dt.

Тогда

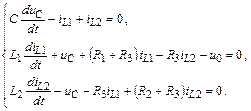
Полученную неоднородную систему линейных дифференциальных уравнений можно записать относительно производных от переменных состояния 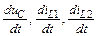в нормальной форме:

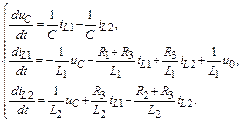
Матричная форма записи полученной системы уравнений переменных состояния имеет вид

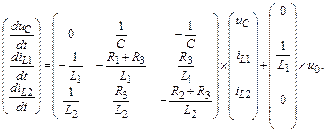
Приложение 2