Сукупність усіх раціональних та ірраціональних чисел звуть дійсними числами

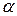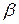Усі дійсні числа впорядковані за величиною, тобто для будь-яких двох чисел і справедливе одне з трьох співвідношень ; ; .

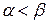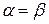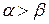Абсолютна вартість числа.

Абсолютною вартістю (або модулем) числа а зветься арифметична вартість цього числа

.

.

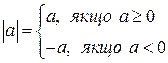
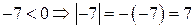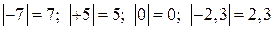Властивості:

За самим означенням

1. .

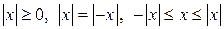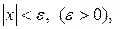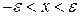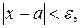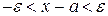2. Якщо то . Зокрема, коли то або .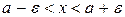

3. .

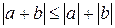Доведення: Запишемо очевидні нерівност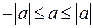і: і 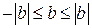. Додамо їх почленно

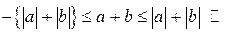(рівносильне) .

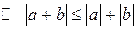Метод математичної індукції поширює цю властивість на любу кількість доданків.

4. .

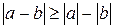(Абсолютна вартість різниці не менша різниці абсолютних вартостей цих чисел).

Доведення: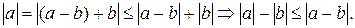

Рівност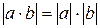і і 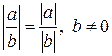майже очевидні і на них спинятися не будемо.

Сталі і змінні величини.

Величина зветься змінною, якщо вона може набирати різні числові вартості в умовах даної задачі.

Сталою величиною звуть величину, яка має цілком певну вартість в умовах даної задачі або за будь-яких умов.

Область змінювання змінної величини. Сукупність усіх числових вартостей, що їх може набувати змінна х, звуть областю чи обсягом змінювання цієї змінної.

Приклад – радіус кола: .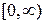

Функціональна залежність.

При дослідженні різноманітних явищ нас цікавлять не стільки змінні величини, взяті кожна окремо, скільки зв’язок між ними та залежність одних величин від інших.

Абстрагуючись від конкретних залежностей між конкретними величинами, дамо означення функції.

Нехай Х і У – деякі числові множини, а х і у – числа, які їм належать.

Змінна у зветься функцією змінної х, якщо будь-якій вартості х є Х за деяким правилом чи законом ставиться у відповідність одна певна вартість

у є У.

Це означення однозначної функції.

Коли у відповідність х ставиться 2 чи більше вартостей у, то у звуть дво- або багатозначною функцією.

Змінна х – аргумент, або незалежна змінна, у – функція, або залежна змінна. Символічний запис

.

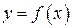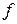- характеристика функції, вона позначає те правило чи закон, який визначає у як функцію від х.

Множина Х – область визначення функції, У – множина її значень.

Функція, яка визначається з функціональної залежності 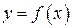, коли в ній розглядати у як аргумент, а х – як функцію, тобто функція 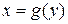зветься оберненою щодо даної функції .

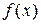Дану функцію 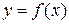часто звуть прямою. Очевидно, функці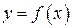ї і 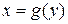є взаємно обернені. Наприклад, 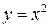– пряма функція, а 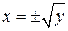– їй обернена. Остання є двозначною.

Окремі вартості функції 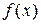при 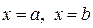і т.п. позначають символами .

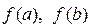Приклад 1. 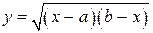, 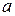і 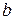– дійсні, 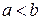. Функція визначена для таких вартостей х, які справджують нерівності 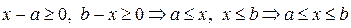. Таким чином, для всіх вартостей х, між 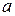та 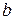включаючи 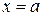та 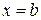, функція у має дійсні вартості. Тут Х – це 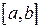– замкнений проміжок.

Приклад 2. 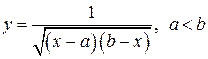. Функція визначена при 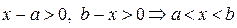, або 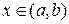. Тут Х – відкритий проміжок, або інтервал .

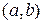Відкритий проміжок, для якого дана точка, а є його серединою (центром) зветься околом цієї точки.

Всі точки х, які справджують нерівність 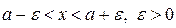, складають окіл точки 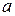з довжиною .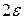