Прямая система дифференциальных уравнений
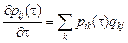
с начальными условиями 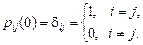
Иногда удобно записывать системы уравнений Колмогорова в матричной форме. Введем матрицу вероятностей переходов 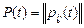 для однородной цепи Маркова с непрерывным временем и конечным числом состояний, тогда системы уравнений можно записать в виде
для однородной цепи Маркова с непрерывным временем и конечным числом состояний, тогда системы уравнений можно записать в виде
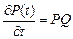 – прямая,
– прямая,
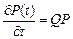 – обратная.
– обратная.
Обратная система уравнений применяется обычно для нахождения значений функционалов от цепей Маркова, прямую систему уравнений можно применять для нахождения безусловного распределения вероятностей 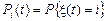 состояний системы в произвольный момент времени.
состояний системы в произвольный момент времени.
Пример. Пусть 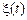 является однородной цепью Маркова с двумя состояниями,
является однородной цепью Маркова с двумя состояниями, 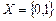 . Время пребывания в состоянии
. Время пребывания в состоянии 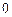 распределено по экспоненциальному закону с параметром
распределено по экспоненциальному закону с параметром 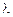 ,а время пребывания в состоянии
,а время пребывания в состоянии 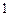 распределено по экспоненциальному закону с параметром
распределено по экспоненциальному закону с параметром 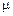 . Составить прямую и обратную системы дифференциальных уравнений Колмогорова. Найти матрицу вероятностей переходов из состояния
. Составить прямую и обратную системы дифференциальных уравнений Колмогорова. Найти матрицу вероятностей переходов из состояния 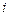 в
в 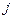 ,
, 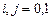 .
.
Решение:
Пусть 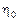 – случайная величина, характеризующая время пребывания в состоянии
– случайная величина, характеризующая время пребывания в состоянии 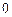 , тогда
, тогда 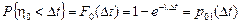 –вероятность того, что цепь Маркова за время
–вероятность того, что цепь Маркова за время 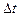 перейдет из состояния
перейдет из состояния 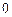 в состояние
в состояние  ,а
,а 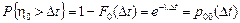 – вероятность того, что цепь Маркова за время
– вероятность того, что цепь Маркова за время 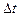 не изменит своего состояния.
не изменит своего состояния.
Аналогично, пусть 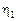 – случайная величина, характеризующая время пребывания в состоянии
– случайная величина, характеризующая время пребывания в состоянии  , тогда
, тогда
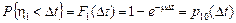 ,
,
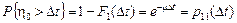 .
.
Находим матрицу инфинитезимальных характеристик 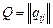 :
:
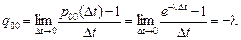 ,
,
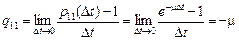 ,
,
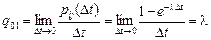 ,
,
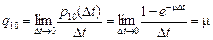 .
.
Составим прямую систему дифференциальных уравнений Колмогорова:
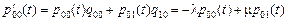 (1)
(1)
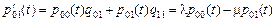 (2)
(2)
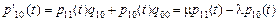 (3)
(3)
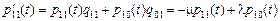 (4)
(4)
Обратная система дифференциальных уравнений Колмогорова будет иметь вид:
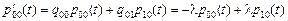 ,
,
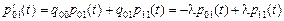 ,
,
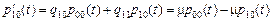 ,
,
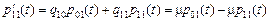 .
.
Начальные условия: 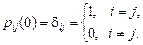
Решая пары уравнений (1-2) и (3-4) находим искомые вероятности. Из первого уравнения получаем 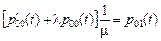 , подставляем в (2):
, подставляем в (2):
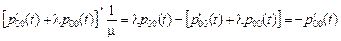 ,
,
получаем дифференциальное уравнение второго порядка:
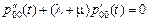 .
.
Откуда находим 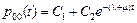 и, учитывая начальные условия, получаем
и, учитывая начальные условия, получаем 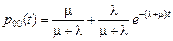 ,
,
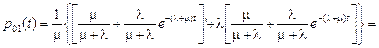
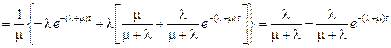 .
.
Аналогично, находим
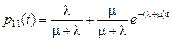 ,
,
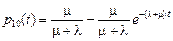 .
.
Задание: убедитесь, что полученное решение обращает в тождество и обратную систему дифференциальных уравнений Колмогорова.
Для рассмотренного примера решим задачу нахождения безусловных вероятностей 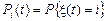 состояний системы в произвольный момент времени.
состояний системы в произвольный момент времени.
Для вероятностей 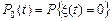 и
и 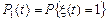
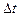 – методом составим прямую систему Колмогорова. Учитывая, что
– методом составим прямую систему Колмогорова. Учитывая, что
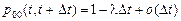 ,
,
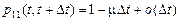 ,
,
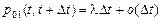 ,
,
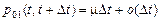 ,
,
имеем
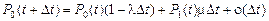
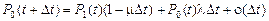 .
.
Разделив полученные выражения на 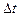 , и устремив
, и устремив 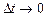 , получим систему дифференциальных уравнений вида
, получим систему дифференциальных уравнений вида
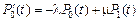
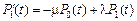 .
.
Пусть в начальный момент цепь Маркова находилась в состоянии 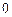 , то есть
, то есть 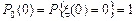 ,
, 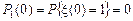 . Тогда решение системы дифференциальных уравнений принимает вид:
. Тогда решение системы дифференциальных уравнений принимает вид:
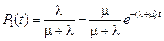 ,
,
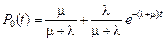 .
.
