Сызықты теңдеулер жүйесін шешу әдістері.

Сызықты емес теңдеулерді сандық шешу әдістері. Жартылай екіге бөлу әдістері

Сызықты емес теңдеулерді шешу.

Ғылыми зерттеу жұмыстарындағы ең жиі кездесетін мәселе

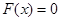(10.1)

түріндегі сызықты емес теңдеулерді шешу, мұндағы 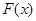- алгебралық та, трансценденттік өрнектен тұратын сызық емес функция. Сызықты емес теңдеулерді шешу екі қадамнан тұрады: түбір жатқан аралықтарды анықтау және түбірлерді табу.

Аралықтарды анықтау. Бұл қадамда тек ғана бір түбір жататын аралықтарды анықтаймыз. Келесі қадамда табылған аралықтардағы түбірлерді табамыз.

(10.1) теңдеуінің 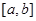аралығында түбірі болу үшін келесі шарт орындалуы тиіс

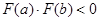(10.2)

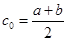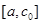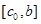Бисекция (кесіндіні жартылай бөлу ) әдісі.Бұл әдісте түбірдің алғашқы жуықтауы ретінде нүктесі алынады. Пайда болған екі аралықтан және (10.2) шарт бойынша тек түбір жатқан аралық алынады. Осы процедураны 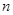рет қайталаймыз, яғни түбір жатқан аралықты 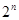рет кішірейтеміз. Интерацияны 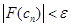болғанша жүргіземіз, мұндағы 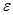-берілген өте аз шама болып табылады.

Хорда әдісі.Бұл жағдайда түбірдің алғашқы жуықтауы ретінде АВ хордасының абцисса осімен қиылысу нүктесі алынады. Қиылысу нүктесінің координатасы 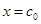және 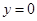, онда АВ хордасының теңдеуінен

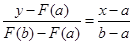(10.3)

теңдеудің түбірін табамыз:

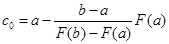. (10.4)

Әрі қарай пайда болған 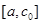және 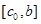аралықтарынан (10.2) шарт бойынша түбір жатқан аралықты ғана таңдап аламыз. Жоғардағы айтылған тәсіл бойынша келесі жуықтауды 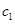табамыз, сөйтіп әрі қарай 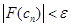болғанға дейін қайталай береміз.

Ньютон әдісі.Бұл әдістің жоғардағы айтылып кеткен әдістерден ерекшелігі, түбір жатқан аралықтан берілуі міндетті емес, тек түбірдің алғашқы жуықтауы 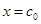берілсе болғаны. Жуық түбір болып, бірінші қадам бойынша табылған 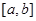аралығының бір шеті алынуы мүмкін. Келесі жуық түбір болып 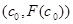нүктесінен 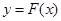қисығына жүргізілген жанаманың абцисса осімен қиылысу нүктесі алынады.

Жанаманың теңдеуі келесі түрде жазылады:

.

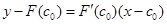Бұл жерден екінші жуықтау бойынша анықталатын 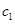түбірді табуға болады:

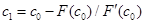
Келесі жуықтаулар төмендегі формула бойынша есептелінеді:

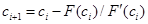. (10.5)

Интерациялық процесс 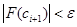шарты орындалғанға дейін жүреді.

Сызықты теңдеулер жүйесін шешу әдістері.

Физикадағы көптеген практикалық есептер сызықты теңдеулер жүйесін шешуге негізделген. Мысалы:

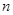теңдеулер жүйесінен тұратын жүйені жазайық:

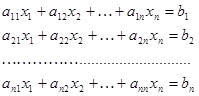(11.1)

Жүйе коэффициенттерінің жиынтын кесте түрінде жазамыз:

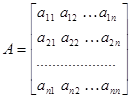
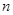-ші ретті матрицаның анықтауышы деп, келесі шама айтамыз:

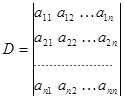
Сызықты теңдеулер жүйесінінің шешімі болу үшін 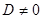болуы тиіс.

Сызықты теңдеулер жүйесін шешу негізгі екі топқа бөлінеді: тікелей есептеу және итерациялық. Тікелей әдістерге Крамер және Гаусс әдістері жатады.Итерациялық әдістерге Гаусс-Зейдель әдісі жатады.

Гаусс әдісі.Бұл әдіс жүйе матрицасын үш бұрышты түрге келтіруге негізделген. Гаусс әдісі екі әдістен тұрады: тура және кері әдіс. Тура әдісте белгісіз айнымалыларды біртіндеп жоямыз да, соңғы теңдеуден 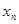-ға байланысты мүшені қалдырамыз. Кері әдісте соңғы теңдеуден 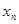-ді тауып, әрі қарай 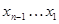белгісіз айнымалыларды табамыз.

Келесі жүйе үшін Гаусс әдісін қарастырамыз

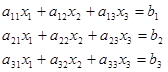(11.2)

2-ші теңдеудегі 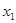-ді жою үшін 1-ші теңдеуді 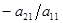-ге көбейтіп, 2-ші теңдеуге қосамыз. Сосын 1-ші теңдеуді 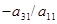көбейтіп 3-ші теңдеуге қосамыз. Сөйтіп келесі теңдеулер жүйесін аламыз:

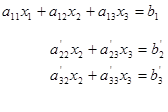(11.3)

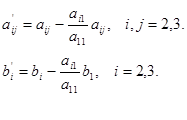
Енді (11.3) жүйенің 3-ші теңдеуінен 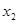-ні алып тастау үшін (11.3) жүйенің 2-ші теңдеуін 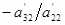-ге көбейтіп 3-ші теңдеуге қосамыз. Келесі теңдеулер жүйесін аламыз:

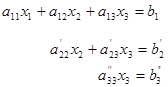(11.4)

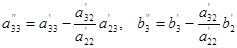
(11.4)-ші жүйенің матрицасы үшбұрышты күйге келді. Осымен Гаусстың тура әдісі аяқталады.

Әрі қарай кері әдіс бойынша (11.4) жүйеден : .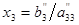

Осы табылған мән арқылы 2-ші теңдеуден 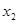-ні, ал 1-ші теңдеуден 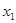-ді табамыз:

.
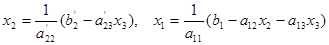