Теорема. (Достаточные условия экстремума)

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

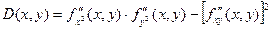
1) Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

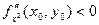- максимум, если 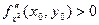- минимум.

2) Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая находит критические точки функции двух переменных, определяет характер экстремума, находит значение функции в точках экстремума.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Условный экстремум.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение

j(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

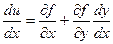
В точках экстремума:

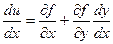=0 (1)

Кроме того:

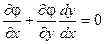(2)

Умножим равенство (2) на число l и сложим с равенством (1).

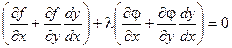
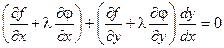
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

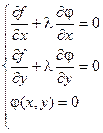
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

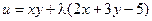
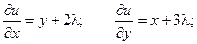
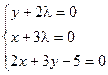
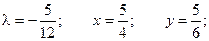
Таким образом, функция имеет экстремум в точке .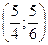

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.

Производная по направлению.

Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М₁( x + Dx, y + Dy, z + Dz).

Проведем через точки М и М₁ вектор 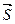. Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются направляющими косинусамивектора .

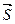Расстояние между точками М и М₁ на векторе 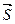обозначим DS.

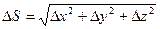
Высказанные выше предположения, проиллюстрируем на рисунке:

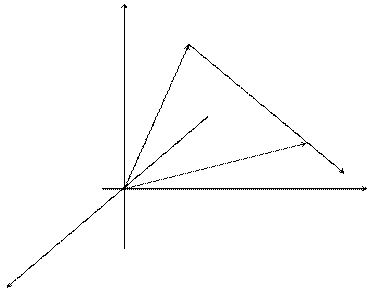z

M

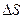
M₁

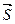
y

x

Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:

,

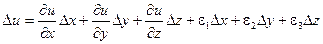где величины e₁, e₂, e₃ – бесконечно малые при .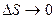

Из геометрических соображений очевидно:

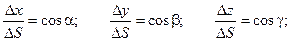
Таким образом, приведенные выше равенства могут быть представлены следующим образом:

;

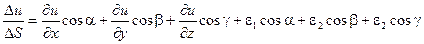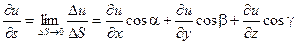
Заметим, что величина s является скалярной. Она лишь определяет направление вектора .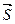

Из этого уравнения следует следующее определение:

Определение: Предел 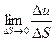называется производной функции u(x, y, z) по направлению вектора 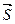в точке с координатами ( x, y, z).

Поясним значение изложенных выше равенств на примере.

Пример. Вычислить производную функции z = x² + y²x в точке А(1, 2) по направлению вектора 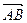. В (3, 0).

Решение. Прежде всего необходимо определить координаты вектора .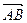

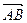=(3-1; 0-2) = (2; -2) = 2 .

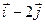Далее определяем модуль этого вектора:

=

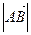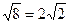
Находим частные производные функции z в общем виде:

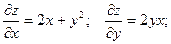
Значения этих величин в точке А :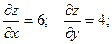

Для нахождения направляющих косинусов вектора 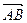производим следующие преобразования:

=

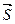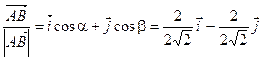
За величину 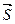принимается произвольный вектор, направленный вдоль заданного вектора, т.е. определяющего направление дифференцирования.

Отсюда получаем значения направляющих косинусов вектора :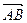

cosa = 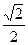; cosb = -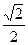

Окончательно получаем: 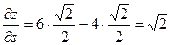- значение производной заданной функции по направлению вектора .

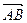Градиент.

Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке

,

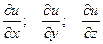то этот вектор называется градиентомфункции u.

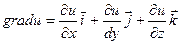
При этом говорят, что в области D задано поле градиентов.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая находит градиент и производную по направлению для любой функции трех переменных в любой точке.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Связь градиента с производной по направлению.

Теорема: Пусть задана функция u = u(x, y, z) и поле градиентов

.

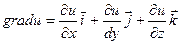Тогда производная 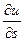по направлению некоторого вектора 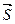равняется проекции вектора gradu на вектор .

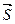Доказательство: Рассмотрим единичный вектор 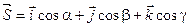и некоторую функцию u = u(x, y, z) и найдем скалярное произведение векторов 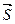и gradu.

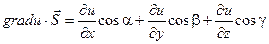
Выражение, стоящее в правой части этого равенства является производной функции u по направлению s.

Т.е. 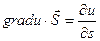. Если угол между векторами gradu и 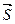обозначить через j, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор 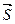единичный, т.е. его модуль равен единице, можно записать:

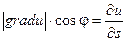
Выражение, стоящее в правой части этого равенства и является проекцией вектора gradu на вектор .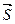

Теорема доказана.

Для иллюстрации геометрического и физического смысла градиента скажем, что градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой- либо точке. В физике существуют такие понятия как градиент температуры, градиент давления и т.п. Т.е. направление градиента есть направление наиболее быстрого роста функции.

С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции.

Кратные интегралы.

Как известно, интегрирование является процессом суммирования. Однако суммирование может производится неоднократно, что приводит нас к понятию кратных интегралов. Рассмотрение этого вопроса начнем с рассмотрения двойных интегралов.

Двойные интегралы.

Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой

f(x, y) = 0.

y

0 x

Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область D.

С геометрической точки зрения D - площадь фигуры, ограниченной контуром.

Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dх_i, а по оси у – на Dу_i. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.

Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны S_i = Dx_i × Dy_i .

В каждой частичной области возьмем произвольную точку Р(х_i, y_i) и составим интегральную сумму

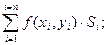
где f – функция непрерывная и однозначная для всех точек области D.

Если бесконечно увеличивать количество частичных областей D_i, тогда, очевидно, площадь каждого частичного участка S_i стремится к нулю.

Определение: Если при стремлении к нулю шага разбиения области D интегральные суммы 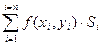имеют конечный предел, то этот предел называется двойным интеграломот функции f(x, y) по области D.

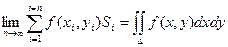
С учетом того, что S_i = Dx_i × Dy_i получаем:

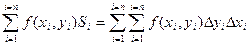
В приведенной выше записи имеются два знака S, т.к. суммирование производится по двум переменным х и у.

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

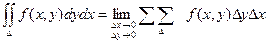
Условия существования двойного интеграла.

Сформулируем достаточные условия существования двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл 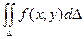существует.

Теорема. Если функция f(x, y) ограничена в замкнутой области D и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл 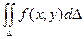существует.

Свойства двойного интеграла.

1)

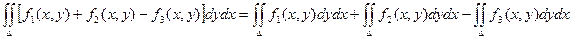
2)

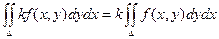
3) Если D = D₁ + D₂, то

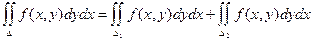
4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

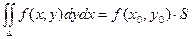
5) Если f(x, y) ³ 0 в области D, то .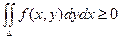

6) Если f₁(x, y) £ f₂(x, y), то .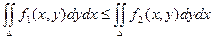

7) .

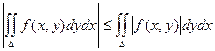Вычисление двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и

j £ y, тогда

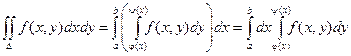
y y = y(x)

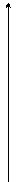D

y = j(x)

a b x

Пример. Вычислить интеграл 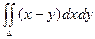, если область D ограничена линиями: y = 0, y = x², x = 2.

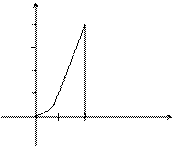y

D

0 2 x

=

=

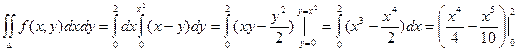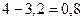
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то

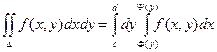
Пример. Вычислить интеграл 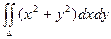, если область D ограничена линиями y = x, x = 0, y = 1, y = 2.

y

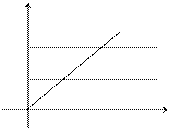y = x

D

0 x

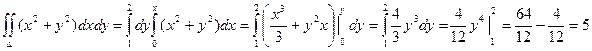
Пример. Вычислить интеграл 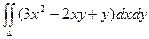, если область интегрирования D ограничена линиями х = 0, х = у², у = 2.

=

=

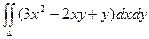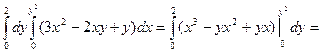
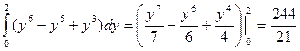
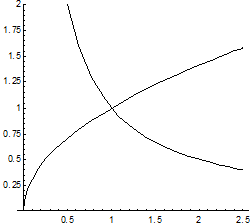
Пример. Вычислить двойной интеграл 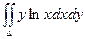, если область интегрирования ограничена линиями ху=1, у = 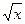, х = 2.

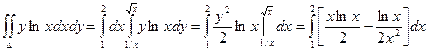
1.

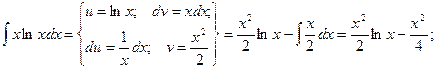
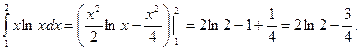
2.

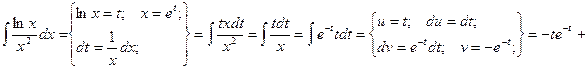
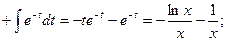
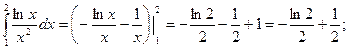
3.

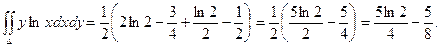
При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая вычисляет двойной интеграл от любой функции.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Замена переменных в двойном интеграле.

Расмотрим двойной интеграл вида 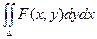, где переменная х изменяется в пределах от a до b, а переменная у – от j₁(x) до j₂(х).

Положим х = f(u, v); y = j(u, v)

Тогда dx = 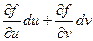; dy = ;

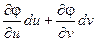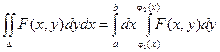
т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.

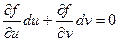, т.е.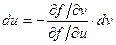

пожставляя это выражение в записанное выше соотношение для dy, получаем:

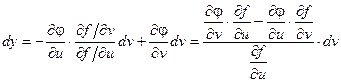
Выражение 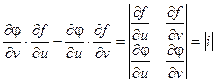называется определителем Якобиили Якобианомфункций f(u, v) и j(u, v).

(Якоби Карл Густав Якоб – (1804-1851) – немецкий математик)

Тогда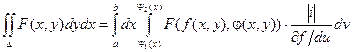

Т.к. при первом интегрировании приведенное выше выражение для dx принимает вид 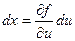( при первом интегрировании полагаем v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:

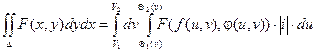
Двойной интеграл в полярных координатах.

Воспользуемся формулой замены переменных:

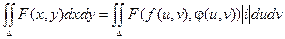
При этом известно, что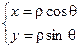

В этом случае Якобиан имеет вид:

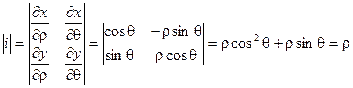
Тогда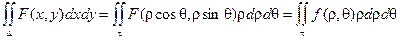

Здесь t - новая область значений,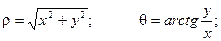

Тройной интеграл.

При рассмотрении тройного инеграла не будем подробно останавливаться на всех тех теоретических выкладках, которые были детально разобраны применительно к двойному интегралу, т.к. существенных различий между ними нет.

Единственное отличие заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в техмерном пространстве.

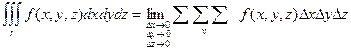
Суммирование производится по области v, которая ограничена некоторой поверхностью j(x, y, z) = 0.

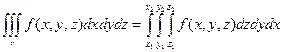
Здесь х₁ и х₂ – постоянные величины, у₁ и у₂ – могут быть некоторыми функциями от х или постоянными величинами, z₁ и z₂ – могут быть функциями от х и у или постоянными величинами.

Пример. Вычислить интеграл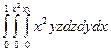

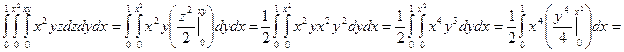
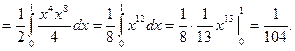
Замена переменных в тройном интеграле.

Операция замены переменных в тройном интеграле аналогична соответсвующей операции для двойного интеграла.

Можно записать:

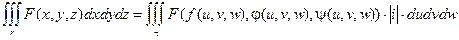
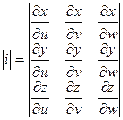
Наиболее часто к замене переменной в тройном интеграле прибегают с целью перейти от декартовой прямоугольной системы координат к цилиндрической или сферической системе. См. Цилиндрическая и сферическая системы координат.

Рассмотрим эти преобразования подробнее.

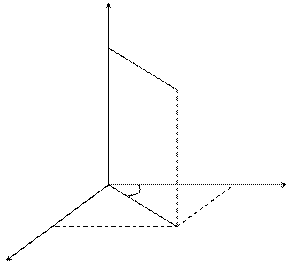
Цилиндрическая система координат.

z

P

z

q x

r

y

Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

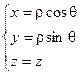
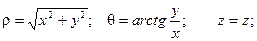
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:

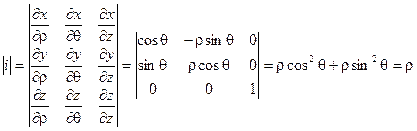
Итого: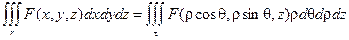

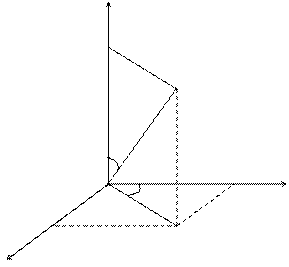
Сферическая система координат.

z

P

r

j

0 q x

y

Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

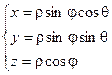
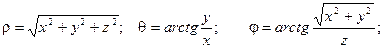
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:

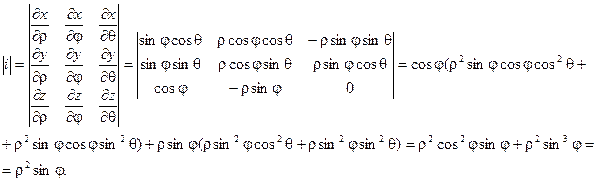
Окончательно получаем:

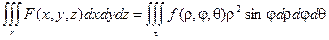
Геометрические и физические приложения кратных интегралов.

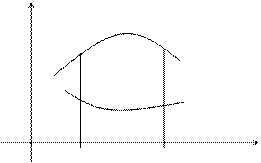
1) Вычисление площадей в декартовых координатах.

y

y = j(x)

S

y = f(x)

a b x

Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:

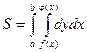
Пример. Вычислить площадь фигуры, ограниченной линиями y² = 4x + 4;

x + y – 2 = 0.

Построим графики заданных функций:

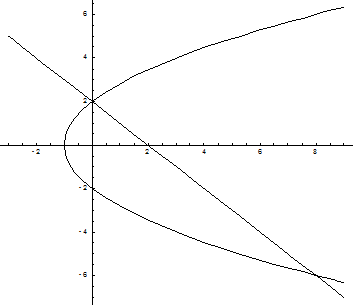
Линии пересекаются в двух точках – (0, 2) и (8, -6). Таким образом, область интегрирования ограничена по оси Ох графиками кривых от 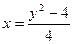до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна:

S =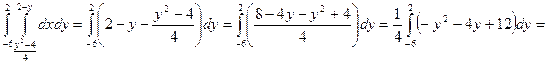

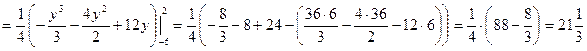
2) Вычисление площадей в полярных координатах.

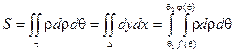
3) Вычисление объемов тел.

Пусть тело ограничено снизу плосткостью ху, а сверху– поверхностью z = f(x,y),

а с боков – цилиндрической поверхностью.

Такое тело называется цилиндроид.

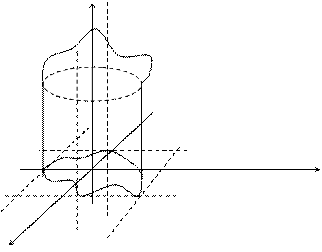z

z = f(x, y)

x₁ y₁ x₂

x

y₂

y

V =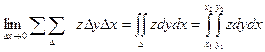

Пример. Вычислить объем, ограниченный поверхностями: x² + y² = 1;

x + y + z =3 и плоскостью ХОY.

Пределы интегрирования: по оси ОХ: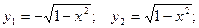

по оси ОY: x₁ = -1; x₂ = 1;

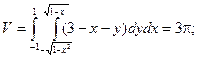
4) Вычисление площади кривой поверхности.

Если поверхность задана уравнением: f(x, y, z) = 0, то площадь ее поверхности находится по формуле:

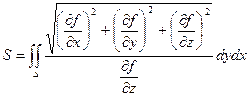
Если поверхность задана в неявном виде, т.е. уравнением z = j(x, y), то площадь этой поверхности вычисляется по формуле:

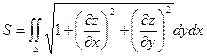
5)Вычисление моментов инерции площадей плоских фигур.

Пусть площадь плоской фигуры (область D) ограничена линией, уравнение которой f(x,y) = 0. Тогда моменты инерции этой фигуры находятся по формулам:

- относительно оси Ох: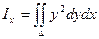

- относительно оси Оу: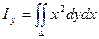

- относительно начала координат: 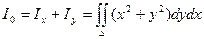- этот момент инерции называют еще полярным моментом инерции.

6) Вычисление центров тяжести площадей плоских фигур.

Координаты центра тяжести находятся по формулам:

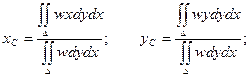
здесь w – поверхностная плотность (dm = wdydx –масса элемента площади).

7) Вычисление объемов тел с помощью тройного интеграла.

Если поверхность тела описывается уравнением f(x, y, z) = 0, то объем тела может быть найден по формуле:

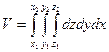
при этом z₁ и z₂ – функции от х и у или постоянные, у₁ и у₂ – функции от х или постоянные, х₁ и х₂ – постоянные.

8) Координаты центра тяжести тела.

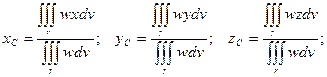
9) Моменты инерции тела относительно осей координат.

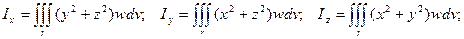
10) Моменты инерции тела относительно координатных плоскостей.

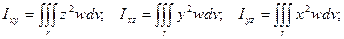
11) Момент инерции тела относительно начала координат.

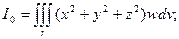
В приведенных выше формулах п.п. 8 – 11 r – область вычисления интеграла по объему, w – плотность тела в точке (х, у, z), dv – элемент объема

- в декартовых координатах: dv = dxdydz;

- в циллиндрических координатах: dv = rdzdjdq;

- в сферических координатах: dv = r²sinjdrdjdq.

12) Вычисление массы неоднородного тела.

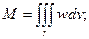
Теперь плотность w – величина переменная.

Содержание КВМ Часть 1.

Содержание КВМ Часть 3.

Содержание КВМ Часть 4.

Содержание:

Дифференциальное исчисление функций одной переменной.

Производная функции, ее геометрический и физический смысл.

Уравнение касательной и нормали к кривой.

Односторонние производные функции в точке.

Основные правила дифференцирования.

Производные основных функций.

Производная сложной функции.

Логарифмическое дифференцирование.

Производная показательно – степенной функции.

Производная обратной функции.

Дифференциал функции.

Геометрический смысл дифференциала.

Свойства дифференциала.

Дифференциал сложной функции. Инвариантная форма записи.

Формула Тейлора.

Формула Лагранжа.

Формула Маклорена.

Представление функций по формуле Тейлора.

Бином Ньютона.

Применение дифференциала к приближенным вычислениям.

Теоремы о среднем.

Теорема Ролля.

Теорема Лагранжа.

Теорема Коши.

Раскрытие неопределенностей. Правило Лопиталя.

Производная и дифференциалы высших порядков.

Правила нахождения производных.

Исследование функций.

Возрастание и убывание функций.

Точки экстремума.

Критические точки.

Достаточные условия экстремума.

Исследование функций с помощью производных высших порядков.

Выпуклость и вогнутость кривой.

Точки перегиба.

Асимптоты.

Схема исследования функций.

Векторная функция скалярного аргумента.

Уравнение касательной к кривой.

Свойства производной векторной функции скалярного аргумента.

Уравнение нормальной плоскости.

Параметрическое задание функции.

Окружность.

Эллипс.

Циклоида.

Астроида.

Производная функции, заданной параметрически.

Кривизна плоской кривой.

Угол смежности.

Средняя кривизна.

Кривизна дуги в точке.

Радиус кривизны.

Центр и круг кривизны.

Эволюта и эвольвента.

Свойства эволюты.

Кривизна пространственной кривой.

Годограф.

Главная нормаль.

Вектор и радиус кривизны.

Формулы Френе.

Соприкасающаяся плоскость.

Бинормаль.

Кручение кривой.

Интегральное исчисление.

Первообразная функция.

Неопределенный интеграл.

Свойства неопределенного интеграла.

Таблица основных интегралов.

Непосредственное интегрирование.

Способ подстановки.

Интегрирование по частям.

Интегрирование элементарных дробей.

Рекуррентная формула.

Интегрирование рациональных функций.

Интегрирование рациональных дробей.

Метод неопределенных коэффициентов.

Метод произвольных значений.

Интегрирование тригонометрических функций.

Универсальная тригонометрическая подстановка.

Интегрирование иррациональных функций.

Биноминальные дифференциалы.

Тригонометрическая подстановка.

Подстановки Эйлера.

Метод неопределенных коэффициентов.

Интегралы, не выражающиеся через элементарные функции.

Эллиптические интегралы.

Интеграл Пуассона.

Интеграл Френеля.

Интегральный логарифм.

Интегральный синус и косинус.

Определенный интеграл.

Интегральная сумма.

Интегрируемая функция.

Свойства определенного интеграла.

Теорема о среднем.

Обобщенная теорема о среднем.

Вычисление определенного интеграла.

Теорема Ньютона – Лейбница.

Замена переменных в определенном интеграле.

Интегрирование по частям.

Приближенное вычисление определенного интеграла.

Формула прямоугольников.

Формула трапеций.

Формула парабол (Симпсона).

Несобственные интегралы.

Абсолютная сходимость интеграла.

Интеграл от разрывной функции.

Нахождение площадей плоских фигур.

Нахождение площади криволинейного сектора.

Вычисление длины дуги кривой.

Вычисление объемов тел по поперечным сечениям.

Вычисление объемов тел вращения.

Площадь поверхности тела вращения.

Функции нескольких переменных.

Предел.

Непрерывность.

Наибольшее и наименьшее значения.

Частное приращение.

Частная производная.

Геометрический смысл частных производных.

Полное приращение и полный дифференциал.

Касательная плоскость и нормаль к поверхности.

Приближенные вычисления с помощью полного дифференциала.

Частные производные и дифференциалы высших порядков.

Экстремум функции нескольких переменных.

Необходимые условия экстремума.

Достаточные условия экстремума.

Условный экстремум.

Функция Лагранжа.

Производная по направлению.

Направляющие косинусы.

Градиент.

Связь градиента с производной по направлению.

Кратные интегралы.

Двойные интегралы.

Условия существования двойного интеграла.

Свойства двойного интеграла.

Вычисление двойного интеграла.

Замена переменных в двойном интеграле.

Якобиан.

Двойной интеграл в полярных координатах.

Тройной интеграл.

Замена переменных в тройном интеграле.

Цилиндрическая система координат.

Сферическая система координат.

Геометрические и физические приложения кратных интегралов.

Ó Ларин Александр Александрович 2000 год. mailto: [email protected]