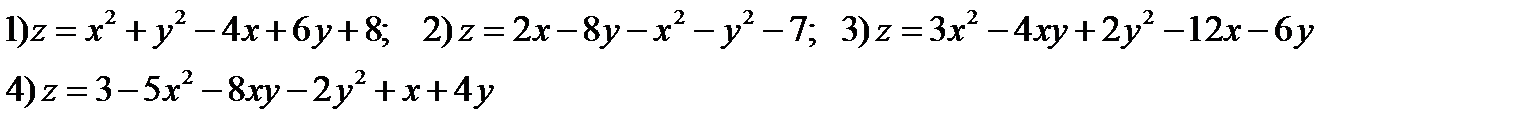Теорема 4.2. достаточные условия существованиялокального экстремума

Тема. Касательная плоскость , нормаль. Экстремумы.

Занятие 5.

Напомним следующие утверждения. Пересечением двух плоскостей

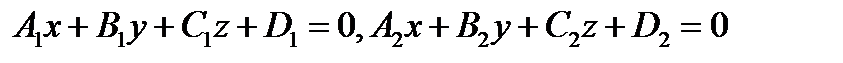является прямая, каждая точка которой

удовлетворяет системе уравнений

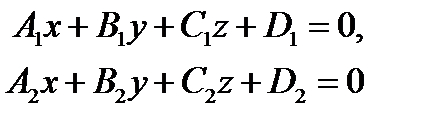(4.1)

Линия, являющаяся пересечением графика функции 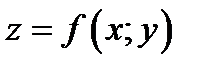и плоскости

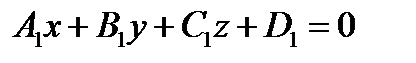задается системой уравнений

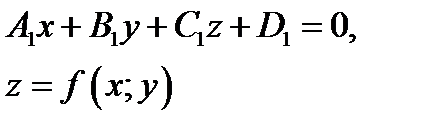(4.2)

График – это поверхность в пространстве. Выберем точку 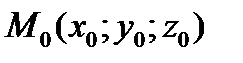принадлежащую графику.

Определение 4.1. Касательной плоскостью к поверхности графика в данной точке 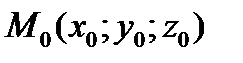называется плоскость, которая содержит все касательные к кривым, проведённым на поверхности графика через эту точку.

Докажем, что уравнение касательной плоскости задаётся уравнением

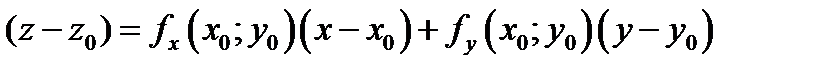(4.3)

Через точку 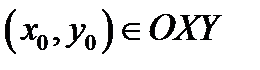проведём в произвольном направлении прямую её уравнение

Z

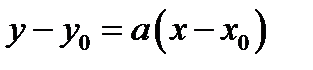имеет вид , где коэффициент 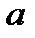- это тангенс угла наклона к оси ОХ. В пространстве 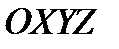это уравнение задаёт плоскость П1 параллельную оси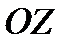

П2

П1

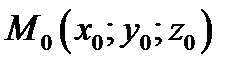
Y

X

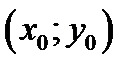
Эта плоскость, пересекаясь с графиком функции, задает кривую , лежащую на графике 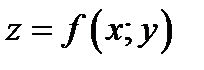. Уравнение кривой имеет вид

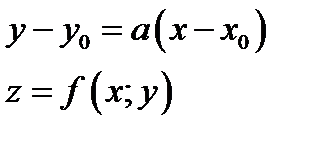(4.4)

Или

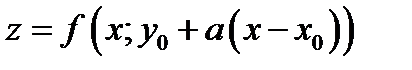(4.5)

Вычисляя производную ( используя цепное правило) по 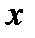в точке 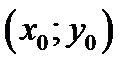получаем 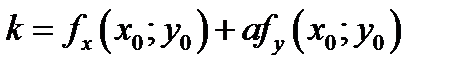наклон касательной прямой L . Касательная прямая L

является пересечением плоскостей П2( 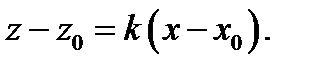)и плоскости П1 в пространстве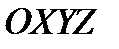

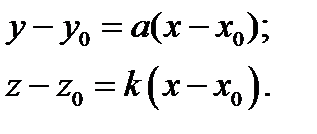
Точка 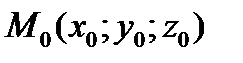лежит на касательной прямой и на плоскости (4.3). Докажем , что касательная целиком лежит на плоскости (4.3):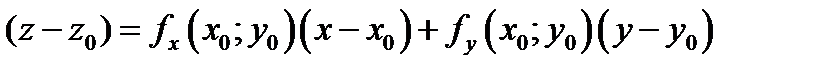

Пусть точка 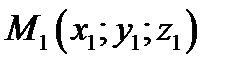лежит на касательной прямой . Докажем, что она лежит на плоскости (4.3). Подставляем координаты точки в уравнение плоскости (4.3)

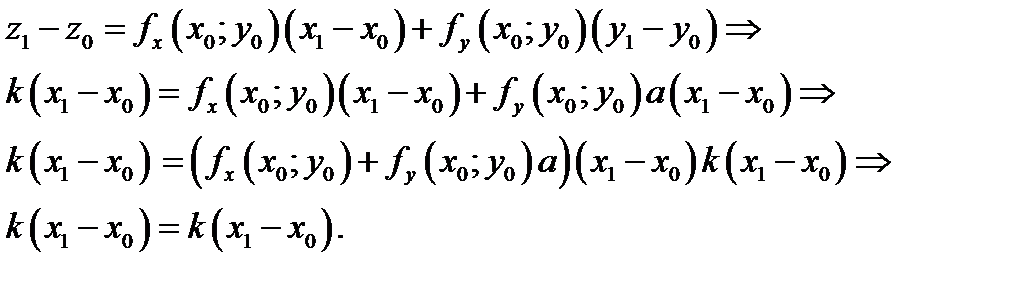
Мы доказали, что точка 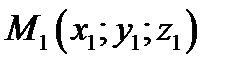лежит на плоскости. Следовательно, если две точки лежат на плоскости, то и вся касательная прямая лежит на плоскости. Поскольку касательная прямая произвольна, то уравнение (5) задаёт, по определению, касательную плоскость.

Если уравнение поверхности задано уравнением, то есть неявно: 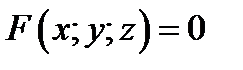(например, эллипсоид или гиперболоид), то уравнение касательной плоскости имеет вид

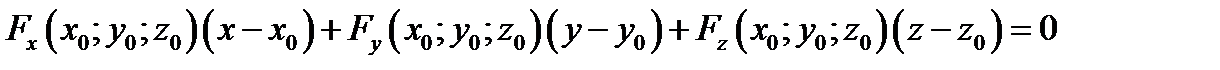(4.6)

Определение 4.2. Нормалью к поверхности в точке 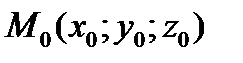называется прямая перпендикулярная к касательной плоскости и проходящая через точку касания .

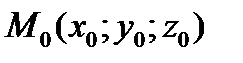Упражнение 1. Найти уравнение касательной плоскости и нормали к поверхности в заданной точке

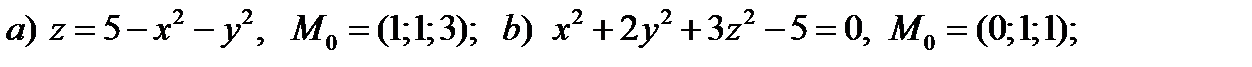
Определение полного дифференциала.

Если функция 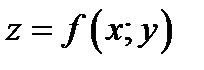дифференцируема в точке 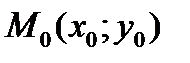, то линейная часть

относительно приращения аргументов ( 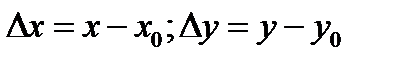) называется полным дифференциалом функции и обозначается

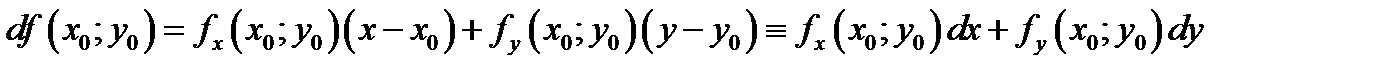(4.7)

Таким образом, имеет место формула линейного приращения функции

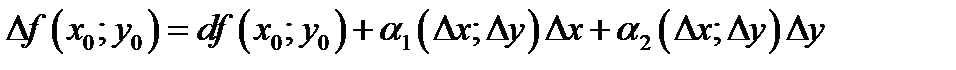(4.8)

Здесь .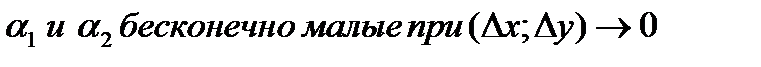

Касательная плоскость наиболее близко примыкает к поверхности в окрестности точки касания.

Упражнение 2. Вычислить приращение функции в точке 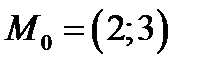относительно приращения аргументов 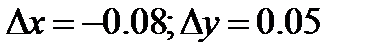. Вычислить её линейную часть (полный дифференциал) и сравнить приращение функции и полный дифференциал.

Локальные экстремумы функции двух переменных

Определение 4.3. Точка называется точкой локального максимума функции 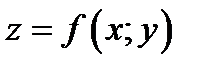, если для всех точек 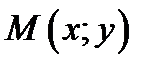,принадлежащих 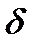-окрестности ,

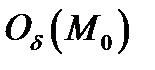справедливо неравенство 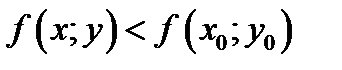(рис.1а)

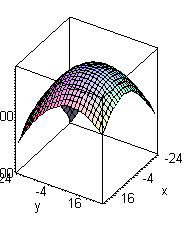
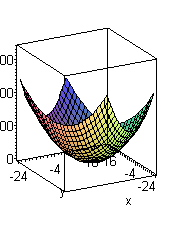
Рис.1а рис1в

Определение 4.4. Точка называется точкой локального минимума функции

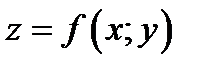, если для всех точек 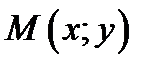,принадлежащих 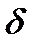-окрестности ,

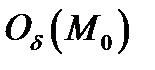справедливо неравенство (рис.1в).

Точки локального максимума или локального минимума функции называются точками экстремума, а локальные максимумы или минимумы функции –экстремумами функции.

Определение 4.5. Точки 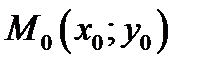, в которых одновременно выполняются условия

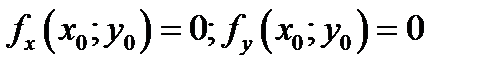(4.8)

Называются стационарными точками.

Теорема 4.1. Любая экстремальная точка дифференцируемой функции – стационарная.

Теорема 4.1 говорит нам, что если нам нужно найти локальные экстремумы у дифференцируемой функции, то сначала нужно найти все её стационарные точки и столько среди них искать точки локальных экстремумов. Критерии отбора точек локальных экстремумов среди стационарных точек у дважды дифференцируемых функций.

ТЕОРЕМА 4.2. ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯЛОКАЛЬНОГО ЭКСТРЕМУМА.

Пусть задана функция 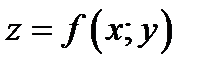у которой все вторые частные производные

непрерывны в . Пусть 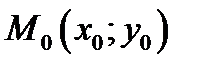-стационарная точка этой функции.

Вычисляем 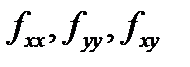в точке 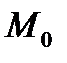и составляем определитель

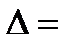
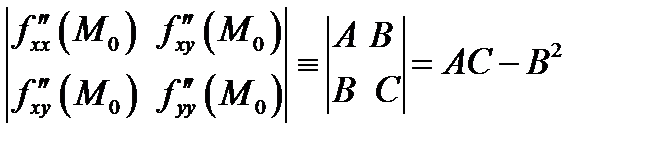(4.9)

ТОГДА СТАЦИОНАРНАЯ ТОЧКА 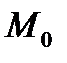БУДЕТ:

1) Точкой локального максимума, если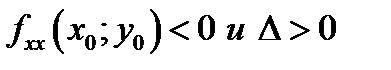

2) Точкой локального минимума, если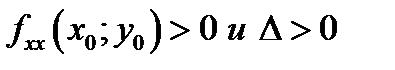

3) не экстремальной точкой , если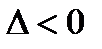

Пример 3.Используя алгоритм, предложенный в теореме 4.2 исследовать функции на экстремум

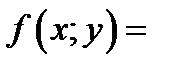
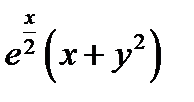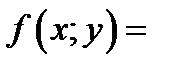
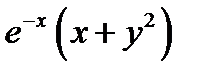1) ; 2) ; 3)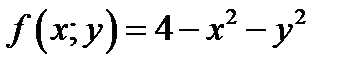

Решение. Решаем 1). Вычислим частные производные

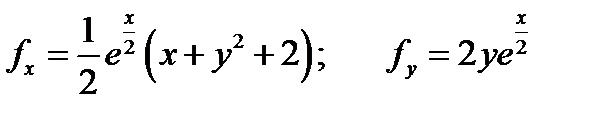
Находим стационарные точки. Для этого решаем систему уравнений

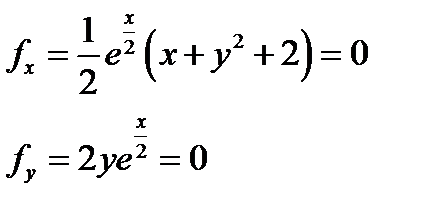
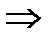
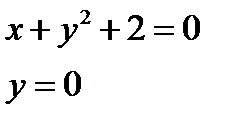
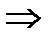
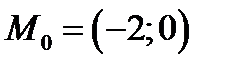
Таким образом существует только одна стационарная точка в которой функция

может достигать экстремума. Вычисляем 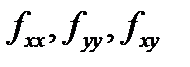в точке 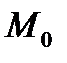и составляем определитель

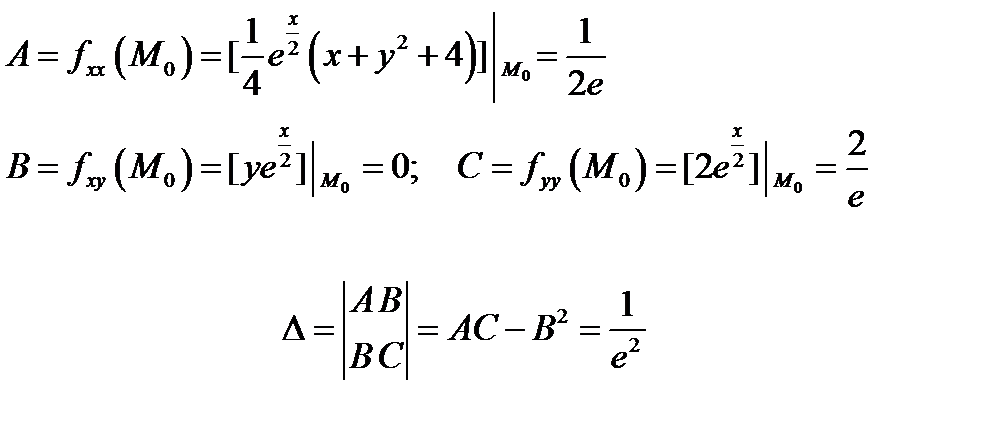
Так как 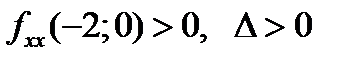, то по теореме 2 пункт 2) точка 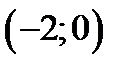-экстремальная.

.

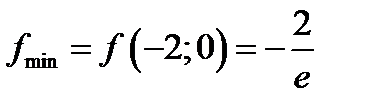Решаем 2). Вычислим частные производные

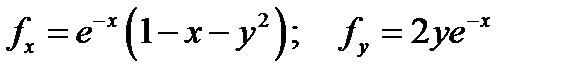
Находим стационарные точки. Для этого решаем систему уравнений

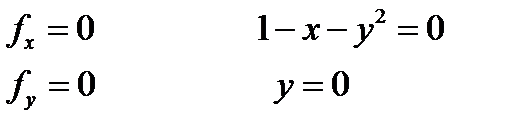
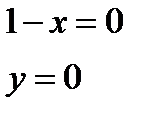
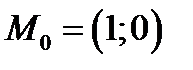
Таким образом существует только одна стационарная точка в которой функция

может достигать экстремума. Вычисляем 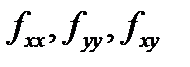в точке 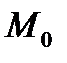и составляем определитель

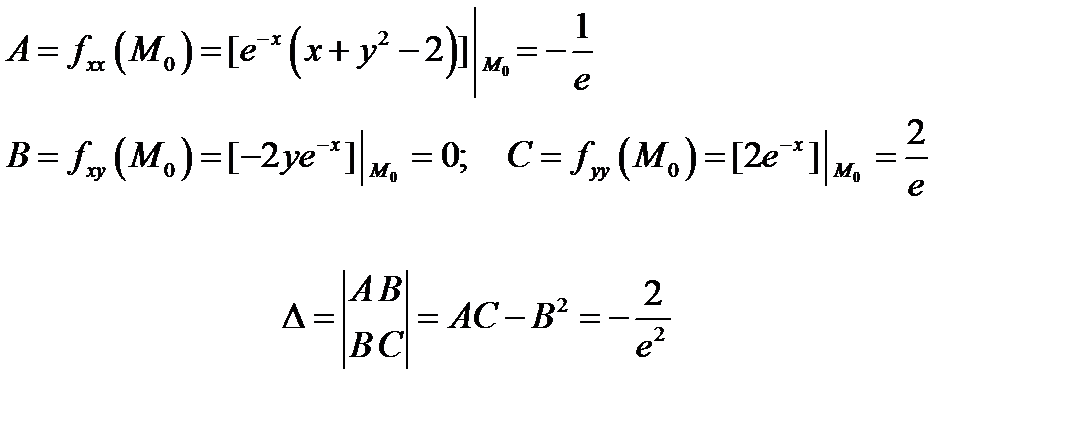
Так как 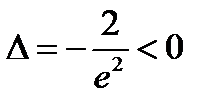, то по теореме 2 пункт 3) в точке 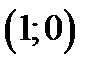нет экстремума.

Решаем 3). Вычислим частные производные

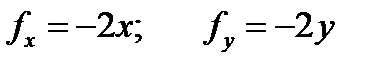
Находим стационарные точки. Для этого решаем систему уравнений

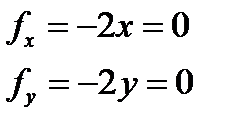
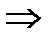
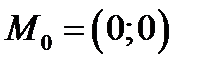
Таким образом существует только одна стационарная точка в которой функция

может достигать экстремума. Вычисляем 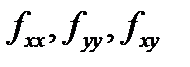в точке 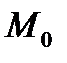и составляем определитель

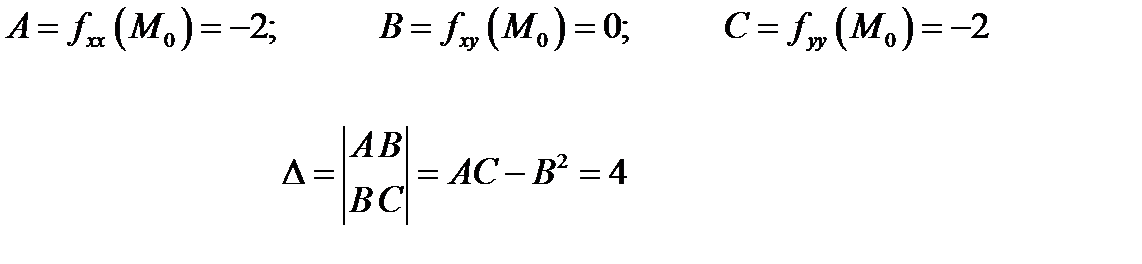
Так как 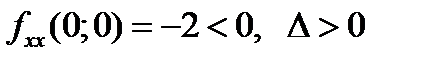, то по теореме 2 пункт 1) точка 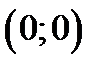-экстремальная.

.

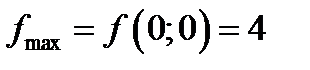Упражнение 3. Исследовать функции на экстремум