Теорема про розклад функції за змінними

Назви елементарних функцій

f ₁ ≡ 0 - функція тотожна “0”

f ₂ ≡ 1 - функція тотожна одиниці

f ₃ ≡ x - тотожна функція

f ₄ = 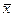- заперечення x

f₅ = x ₁ ٨ x₂ ,(x_1* x₂ ), x₁ @ x₂ , кон’юнкція x₁ і x₂ f₅ = min (x₁ , x₂ )

f₆ = x₁ ٧ x₂ –диз’юнкція x₁ і x₂ ; f₆ = max (x₁,x₂)

f₇ = 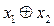–додавання за модулем 2.

f₈ = x₁~ x₂ – x₁ еквівалентне x₂

f₉ = x₁→x₂ - x₁ імплікує x₂

f₁₀ = x₁ ∕ x₂ штрих Шиффера x₁ і x₂ ,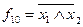

f₁₁= 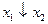- стрілка Пірса x₁ та x₂ ; .

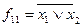Як і у елементарній алгебрі , виходячи із елементарних функцій можна будувати формули.

Множина символів σ ={ך , ٨, ٧, 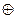, ~, →, ∕ , 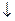} називається множиною логічних зв’язок.

Для скорочення запису приймаються такі домовленості:

· Зовнішні дужки формул не ставляться ;

· Зв’язка ך сильніша за будь-яку двомісну σ

· Зв’язка ٨ сильніша за ٧ , , ~, →, ∕, .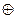

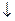Дві булеві функції є рівноцінними, якщо вони набувають однакових значень на всіх можливих наборах своїх аргументів.

Розглянемо множину ٨, ٧, , ∕, , ~, →.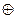

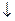Тоді є такі еквівалентності (0 є {٨, ٧, , ∕, , ~}):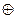

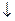x о y = y о x –комутативність зв’язки

(x о y)о z = x о(y о z) асоціативність зв‘язки

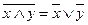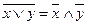і - правила де Моргана

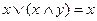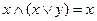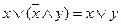; ; ; і 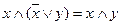правила поглинання.

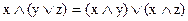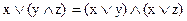; –дистрибутивність диз’юнкції відносно кон’юнкції, та кон’юнкції відносно диз‘юнкції.

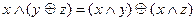–дистрибутивність кон’юнкції відносно додавання по модулю 2 « ».

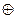Наведемо ще кілька співвідношень:

~ .

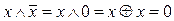
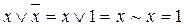
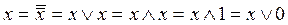
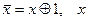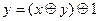Зауважимо, що будь-яку булеву функцію можна побудувати у вигляді формул над множиною зв’язок о ={ ך , ٧,٨} використовуючи так звану досконалу диз’юнктивну нормальну форму.

Істотні та фіктивні змінні

Означення булевих функцій їх рівності не досконале тому, що функції більшого числа змінних може бути замінена функцією меншої кількості змінних. Адже частина змінних може бути фіктивною.

Аргумент функції x_i є істотнім для функції f(x₁,x₂,…x_i-1, x_i,... x_n), якщо існують такі значення α₁ ,…α_i-1, α_i+1...α_n , що

f(α₁,…α_i-1,0,α_i+1,...α_n)≠f(α₁,…α_i-1,1,α_i+1...α_n),

Якщо x_i не є істотною, то вона фіктивна. Дві булеві функції f(x) і y(x) будуть рівними, якщо кожну з них можна отримати з іншої за допомогою введення фіктивних змінних.

Спеціальні види формул.

Диз’юнктивні і кон’юнктивні нормальні форми.

Поліном Жегалкіна.

Формула ,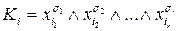

де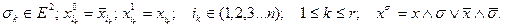

називається кон’юнкцією над множиною змінних .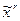

Відповідно 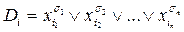називається диз’юнкцією над множиною змінних .

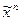Кон’юнкцією (диз’юнкцією) називають елементарною, якщо . Вирази називають буквами.

Число букв в елементарній кон’юнкції (ек) або елементарній диз’юнкції (ед) називають рангом ЕК (ЕД).

Константа “1” називають вираз першого рангу, константа”0” - вираз “0” рангу.

Формула виду D=k₁٧k₂٧...٧k_s, ( k_i для i=1,... s кон’юнкція) називають диз’юнктивною нормальною формою (д.н.ф.).

Формула виду K=D₁٨D₂….٨D_s , ( D_i та i=1,…,s –диз’юнкції) називають кон’юнктивною нормальною формою.(к.н.ф.)

Теорема про розклад функції за змінними

Кожну булеву функцію f (x₁....x_n) при довільному 1 ≤m ≤ n можна зобразити у такій формі:

=

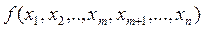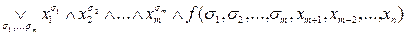
де диз’юнкція береться за всіма можливими наборами значень x₁…x_m.

Таке представлення функції розкладом функції за m змінними.

Приклад 1

Розклад по одній змінній.

.

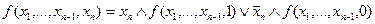Функції f(x₁…x_n-1, 1) та f(x₁ …x_n-1,0) називають компонентами (коефіцієнтами) розкладу.

Приклад2.

Розклад по всіх змінних.

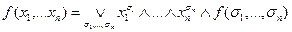
Ясно, що коли 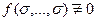, тоді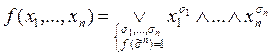

Аналогічно, якщо f {σ_n} 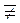1 для всієї сукупності наборів аргументу, то

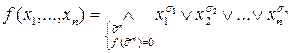
Звернемо увагу, що у приведених формулах кожна змінна входить в елементарну кон‘юнкцію та елементарну диз‘юнкцію лише один раз.