Типы точек покоя. Узел, седло.
Фазовая плоскость.
Дифференциальное уравнение второго порядка
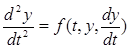 (24.4)
(24.4)
равносильно системе уравнений первого порядка
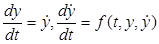 . (24.5)
. (24.5)
Геометрически общее решение уравнения (24.4) или системы (24.5) можно представить семейством фазовых траекторий на фазовой плоскости 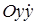 .Особенно удобно такое представление в случае, когда функция
.Особенно удобно такое представление в случае, когда функция 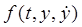 не содержит явным образом независимого переменного t. Тогда система (24.5) имеет вид
не содержит явным образом независимого переменного t. Тогда система (24.5) имеет вид
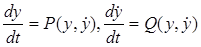 (24.6)
(24.6)
и называется автономной системой. Фазовые траектории в этом случае удовлетворяют дифференциальному уравнению первого порядка
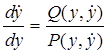 , (24.7)
, (24.7)
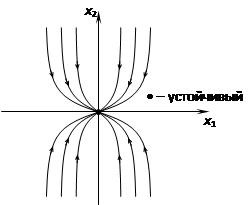 которое каждой точке ставит в соответствие наклон проходящей через нее интегральной кривой. Точки покоя. Точка
которое каждой точке ставит в соответствие наклон проходящей через нее интегральной кривой. Точки покоя. Точка 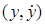 фазовой плоскости системы (24.6) называется обыкновенной точкой, если
фазовой плоскости системы (24.6) называется обыкновенной точкой, если 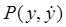 и
и 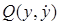 дифференцируемы и не обращаются одновременно в нуль; через каждую обыкновенную точку проходит одна фазовая траектория. Точка
дифференцируемы и не обращаются одновременно в нуль; через каждую обыкновенную точку проходит одна фазовая траектория. Точка 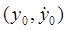 называется особой точкой, если
называется особой точкой, если 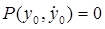 и
и 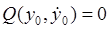 .Замечание. Особые точки классифицируются по характеру фазовых траекторий в их окрестности.Исследование особых точек системы.Если система неоднородная, а ji(t) – ее решение, то с помощью замены yi = xi(t) – ji(t) систему можно свести к однородной, причем решение ji(t) исходной системы будет соответствовать нулевому решению полученной однородной системы. Таким образом, на устойчивость исследуют нулевое решение соответствующей однородной системы. Пусть мы рассматриваем характеристическое уравнение некоторой системы:
.Замечание. Особые точки классифицируются по характеру фазовых траекторий в их окрестности.Исследование особых точек системы.Если система неоднородная, а ji(t) – ее решение, то с помощью замены yi = xi(t) – ji(t) систему можно свести к однородной, причем решение ji(t) исходной системы будет соответствовать нулевому решению полученной однородной системы. Таким образом, на устойчивость исследуют нулевое решение соответствующей однородной системы. Пусть мы рассматриваем характеристическое уравнение некоторой системы: 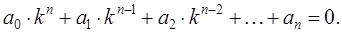 При n=2:
При n=2:
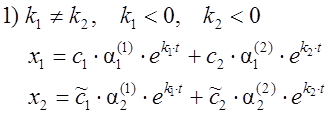 устойчивый узел
устойчивый узел
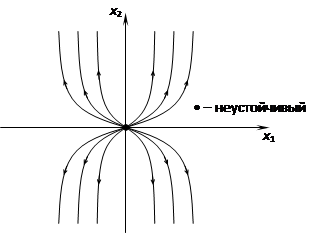 2) k1 ¹ k2, k1 > 0, k2 > 0
2) k1 ¹ k2, k1 > 0, k2 > 0
Неустойчивый узел
 3) k1 ¹ k2, k1 > 0, k2 < 0
3) k1 ¹ k2, k1 > 0, k2 < 0
Седло неустойчивая
Типы точек покоя. Фокус. Центр.
Фазовая плоскость.
Дифференциальное уравнение второго порядка
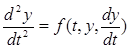 (24.4)
(24.4)
равносильно системе уравнений первого порядка
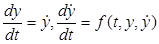 . (24.5)
. (24.5)
Геометрически общее решение уравнения (24.4) или системы (24.5) можно представить семейством фазовых траекторий на фазовой плоскости 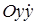 .Особенно удобно такое представление в случае, когда функция
.Особенно удобно такое представление в случае, когда функция 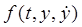 не содержит явным образом независимого переменного t. Тогда система (24.5) имеет вид
не содержит явным образом независимого переменного t. Тогда система (24.5) имеет вид
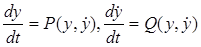 (24.6)
(24.6)
и называется автономной системой. Фазовые траектории в этом случае удовлетворяют дифференциальному уравнению первого порядка
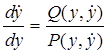 , (24.7)
, (24.7)
 которое каждой точке ставит в соответствие наклон проходящей через нее интегральной кривой. Точки покоя. Точка
которое каждой точке ставит в соответствие наклон проходящей через нее интегральной кривой. Точки покоя. Точка 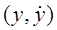 фазовой плоскости системы (24.6) называется обыкновенной точкой, если
фазовой плоскости системы (24.6) называется обыкновенной точкой, если 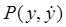 и
и 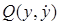 дифференцируемы и не обращаются одновременно в нуль; через каждую обыкновенную точку проходит одна фазовая траектория. Точка
дифференцируемы и не обращаются одновременно в нуль; через каждую обыкновенную точку проходит одна фазовая траектория. Точка 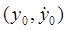 называется особой точкой, если
называется особой точкой, если 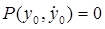 и
и 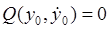 .Замечание. Особые точки классифицируются по характеру фазовых траекторий в их окрестности.Исследование особых точек системы.Если система неоднородная, а ji(t) – ее решение, то с помощью замены yi = xi(t) – ji(t) систему можно свести к однородной, причем решение ji(t) исходной системы будет соответствовать нулевому решению полученной однородной системы. Таким образом, на устойчивость исследуют нулевое решение соответствующей однородной системы. Пусть мы рассматриваем характеристическое уравнение некоторой системы:
.Замечание. Особые точки классифицируются по характеру фазовых траекторий в их окрестности.Исследование особых точек системы.Если система неоднородная, а ji(t) – ее решение, то с помощью замены yi = xi(t) – ji(t) систему можно свести к однородной, причем решение ji(t) исходной системы будет соответствовать нулевому решению полученной однородной системы. Таким образом, на устойчивость исследуют нулевое решение соответствующей однородной системы. Пусть мы рассматриваем характеристическое уравнение некоторой системы: 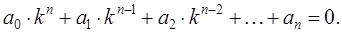 При n=2:
При n=2:
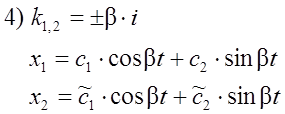 центр(устойчивый) центр(устойчивый)
центр(устойчивый) центр(устойчивый)
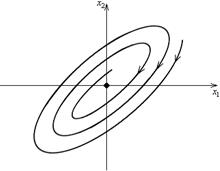
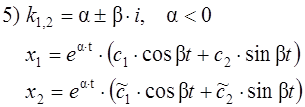
Центр(устойчивый)
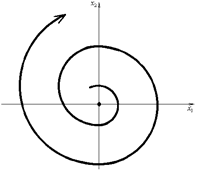
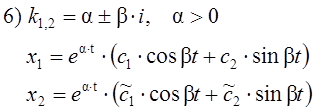
Фокус устойчивый.
 26. Линейные и квазилинейные дифференциальные уравнения в частных производных первого порядка.
26. Линейные и квазилинейные дифференциальные уравнения в частных производных первого порядка.


27. Задача Коши для дифференциальных уравнений в частных производных первого порядка. 
№28. Система дифференциальных уравнений в частных производных 1-го порядка :
Во многих областях науки встречаются системы величин, которые связаны между собой не одним, а сразу несколькими соотношениями , рассматривается задача Коши для систем из двух уравнений с двумя начальными условиями
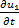 + 8
+ 8 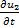 =0,
=0, 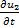 + 2
+ 2 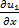 =0 ∞ <x< +∞ 0 <t< ∞
=0 ∞ <x< +∞ 0 <t< ∞
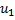 (x, 0) = f(x),
(x, 0) = f(x), 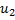 (x, 0) = d(x)
(x, 0) = d(x)
Эта задача может соответствовать определению давления 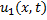 и плотности
и плотности 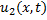 , как функция пространственной координаты x и времени t по известным распределениям этих величин в нач. момент.
, как функция пространственной координаты x и времени t по известным распределениям этих величин в нач. момент.
Запишем систему уравнений в матричной форме
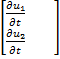 +
+ 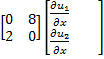 =
= 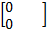
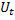 + A
+ A 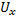 =
= 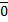 (8.7)
(8.7)
A = 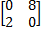
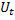 =
= 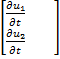
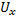 =
= 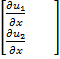
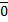 =
= 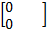
Введение новой неизвестной функции v = 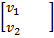 с помощью преобразования u = pv, где p- матрица , по столбцам которой стоят собственные векторы матрицы А.
с помощью преобразования u = pv, где p- матрица , по столбцам которой стоят собственные векторы матрицы А.
Собственные числа матрицы А являются корнями уравнения :
det (A –λ E)=0
или 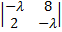 = 0 ó
= 0 ó 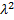 – 16 = 0
– 16 = 0 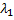 = 4
= 4 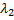 = - 4
= - 4
Найдём собственный вектор 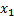 соответствующий собственному значению
соответствующий собственному значению 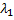 = 4 из системы
= 4 из системы
(A – 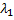 E) (
E) ( 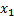 ) = 0
) = 0 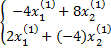
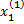 =
= 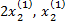 =1 ,
=1 , 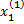 =2 =>
=2 => 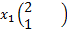 Аналогично найдем вторую СВ,соот-щую
Аналогично найдем вторую СВ,соот-щую 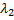 = - 4
= - 4
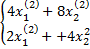
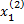 =
= 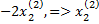 = 1,
= 1, 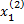 = - 2
= - 2 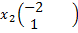 Тогда матрица Р будет иметь вид
Тогда матрица Р будет иметь вид
P= 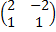
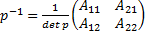 =
= 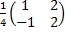 =
= 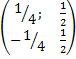 det p= 4
det p= 4
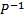 AP =
AP = 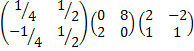 =
= 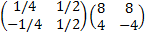 =
= 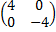 = B
= B
Оказалось, что после замены переменных по формуле u=pv для определения v получится очень простая система два уравнения относительно новых 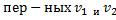 оказываются независимыми .После этого по формуле u=pv находится искомая функция
оказываются независимыми .После этого по формуле u=pv находится искомая функция 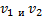 ,но сначала выясним, как выглядит система для определения v ,продифференцировав обе части соотношения по u=pv получаем :
,но сначала выясним, как выглядит система для определения v ,продифференцировав обе части соотношения по u=pv получаем :
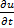 = p
= p 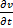
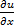 = p
= p 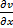 (8.8)
(8.8)
Теперь подставим соотношения (8.8) в систему : 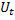 + A
+ A 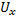 = 0
= 0
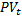 + AP
+ AP 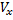 = 0 │*
= 0 │* 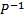
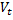 +
+ 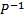 A
A 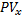 =0;
=0; 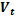 + B
+ B 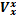 = 0 (8.9)
= 0 (8.9)
Раньше мы уже видели , что B 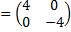
Запишем (8.9) в развернутой форме : 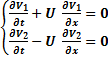 (8.10)
(8.10)
Получилась система из 2х несвязанных уравнений, которые решаются независимо ,их решениями будут : 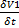 +
+ 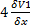 =0
=0
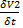 -
- 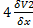 =0
=0 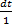 =
= 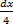 x- 4t =
x- 4t = 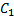
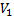 = ϕ (x-4t)
= ϕ (x-4t) 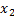 :
: 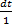 =
= 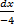 x+4t =
x+4t = 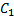
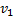 =
= 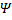 (x+4t)
(x+4t)
Для получения общего решения нужно выполнить по формуле :u=pv 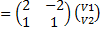
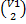 =
= 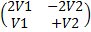 =
= 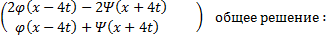
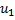 (x, t) =
(x, t) = 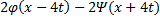
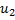 (x, t) =
(x, t) = 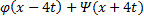
Решается задание Коши:
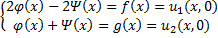 │
│
4 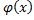 =
= 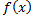 +2
+2 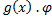 (x) =
(x) = 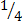 (f(x)+2g(x)) 4 Ψ(x)= 2
(f(x)+2g(x)) 4 Ψ(x)= 2 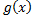
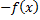 , Ψ(x)=
, Ψ(x)= 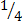 (2g(x)- f(x)) =>
(2g(x)- f(x)) =>
Ответ : 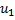 (x, t) =
(x, t) = 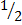 (f(x-4t)+2g(x-4t))-
(f(x-4t)+2g(x-4t))- 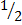 (2g(x+4t)-f(x+4t))
(2g(x+4t)-f(x+4t)) 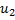 (x, t) =
(x, t) = 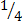 (f(x-4t)+2g(x-4t)+
(f(x-4t)+2g(x-4t)+ 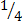 (2g(x+4t)-f(x+4t))
(2g(x+4t)-f(x+4t))
Замечание : часто численные методы ориентированы на решение систем уравнений , а значит многие программы для компьютера написаны так чтобы решить систему уравнений первого порядка, поэтому приходится преобразовывать свое уравнение высшего порядка в систему ур-ний первого порядка.
 29.Построение решения линейного уравнения в виде степенного ряда.
29.Построение решения линейного уравнения в виде степенного ряда.


