Перспектива в неевклидовых пространствах

Статья посвящается преобразованию построений аксонометрии и перспективы с евклидового пространства в неевклидовые. Развитие этой сферы начертательной геометрии даст возможность более точно построить перспективу в пространствах с разными искажениями, которые существуют в нашей вселенной. В ближайшее время, пока масштабные сооружения не строятся на других планетах, эта отрасль геометрии может послужить основой новому направлению в бумажной архитектуре.

Бұл мақала евклидтик емес кеңістіктерде аксонометрия мен перспективаның тұрғызуына арналған. Сызба геометрияның бұл саласы табиғатта кездесетін кеңістіктердегі перспективаны неғұрлым дәл тұрғызуға мүмкіндік береді. Жақын арада басқа ғаламшарда алып ғимараттар салынбаса да, сызба геометрияның осы саласы қағаз сәулетінің жаңа саласына негіз бола алады.

Article is dedicated to the transformation of perspective constructions and prospects with Euclidean space in non-Euclidean, that is distorted space. The development of this field of descriptive geometry will allow a more accurate perspective and perspective to build in spaces with different distortions that exist in our universe. In the near future, while the large-scale structures are not built on other planets, this branch of geometry can serve as a basis for a new direction in the paper architecture.

В давние времена Земля представлялась людям в виде плоского диска, расположенного на китах/слонах/черепахе, либо окруженного океаном и накрытого небесным куполом (рис. 1).

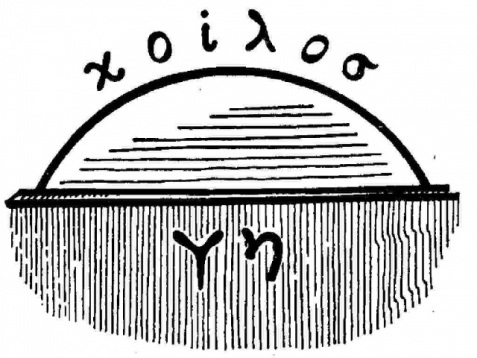
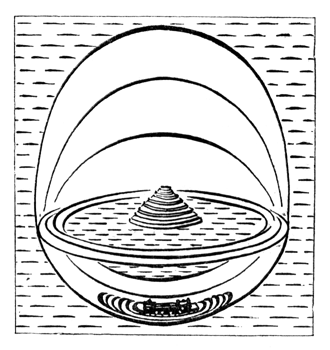
Рис. 1

Но уже у древних греков (Парменид) появились догадки о шарообразности Земли, которые позже основывалась уже на эмпирических наблюдениях (Аристотель)[1].

Однако у тех же греков всё-таки оставались сомнения в шарообразности Земли (Демокрит, Эпикур), а раннехристианский мир даже вернулся к идее плоской Земли. При этом мифологические представления о Земле становились геометризованными. Например, византийский географ VI в. Козьма Индикоплов полагал, что космос подобен прямоугольной призме с цилиндрической аркой над ней (рис. 2) по форме напоминающей библейскую скинию (рис. 3).

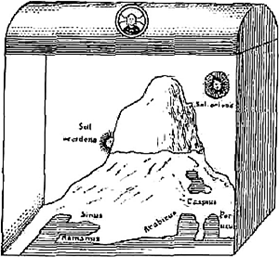
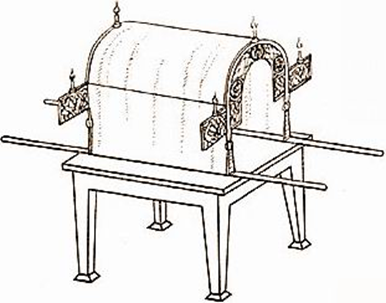
Рис. 2 Рис. 3

Наряду с изменениями во взглядах на форму космоса изменялись и геометрические представления, лежащие в основе системы наглядного отображения пространства.

До XIX в. наглядная геометрия основывалась на евклидовых постулатах. Но с появлением неевклидовой геометрии – геометрии Римана и геометрии Лобачевского-Больяи, а также общей теорией относительности, открылись новые возможности в исследовании восприятия окружающего мира. Теперь оказалось возможным рассчитать искривление пространства и времени, которое влияет на формы, скорость и массы обьектов, а, следовательно, и на особенности их зрительного восприятия и отображения.

Конечно, размер земли очень велик с точки зрения человеческого восприятия, чтобы учитывать искажения, возникающие при восприятии объектов, их наглядном изображении и даже при постройке сооружений. Но если допустить в ближайшем тысячелетии колонизацию других планет, восприятие пространств которых может оказаться весьма искажено (искривлено) для нашего восприятия, обычные евклидовы построения аксонометрии и перспективы уже не будут соответствовать данным пространствам. Тогда придется пересматривать традиционные системы построений аксонометрии и перспективы и другие методы отображения, приспосабливая их для искривленных пространств.

В данной работе перед нами стояла задача – преобразовать построения линейной перспективы и аксонометрии с учетом искажений, свойственных природному пространству, которое определяют как эллиптическое или сферическое, а по сути неевклидово, поскольку оно связано с формой планет, которая чаще всего представляет собою поверхность либо эллипсоида вращения, либо сферы.

Таким образом, приходят к понятию сферической перспективы, в которой изобразительное сферическое пространство соотносится со зрительным центром, совпадающим с геометрическим центром изображения. Представления о подобном пространстве, вероятно, восходят к древнейшим верованиям о центре мира, находящемся в сердцевине земли.

Тенденция к сферичности изобразительного пространства прослеживается на многих произведениях классического искусства. Наиболее четко это можно видеть на изображениях, выполненных в системе обратной перспективы, в которой местоположения зрителя оказывается в глубине изобразительного пространства. Примером могут служить иконописные изображения (рис. 4).

Сферичность пространства хорошо видна в работах П. Брейгеля, который подчеркивал кривизну, характерную неевклидовой геометрии, которая соответствовала мысленному взгляду из космоса (рис. 5).

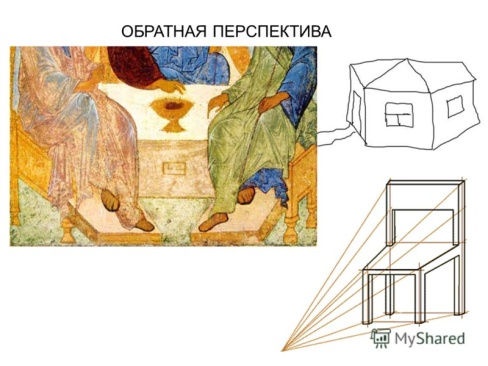
Рис. 4 Рис. 5

Сферические искажения можно наблюдать на сферических зеркалах. При этом глаза зрителя всегда находятся в центре шара (рис. 6). Линия горизонта и главная вертикаль строго прямые, так же как все остальные линии глубины, сходящиеся в главной точке. Все остальные линии не инцидентные центру будут представлять собою полуэллипсы, которые, по мере удаления от главной точки, будут трансформироваться в окружность (рис. 7).

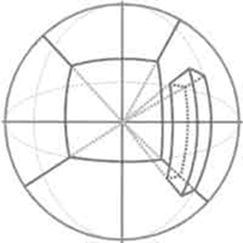
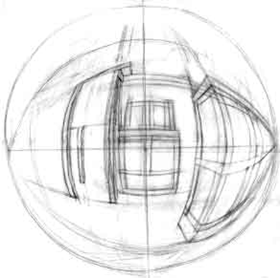
Рис. 6 Рис. 7

Таким образом, вначале нужно преобразовать евклидово пространство в эллиптическое или сферическое, для чего основанием служит гипотеза Пуанкаре, которая гласит: «Всякое односвязное компактное многообразие без края гомеоморфно трехмерной сфере» [2]. Само преобразование происходит таким образом: плоское пространство сначала сворачивается в бесконечно длинный цилиндр или трубу (рис. 8), а затем этот цилиндр смыкается в тор, вначале открытый, а затем закрытый, после чего, уменьшая расстояние от оси вращения тора до центра его меридиана до нуля, можно получить сферу (рис. 9).

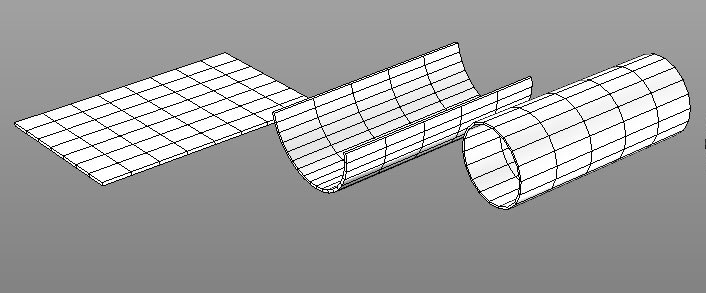
Рис. 8

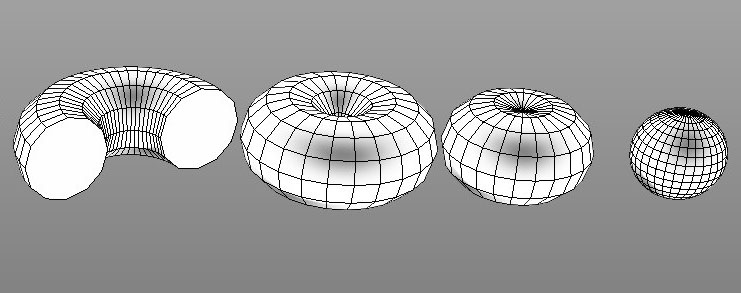
Рис. 9

Все эти пространства (цилиндрические, тороидные, сферические) встречаются в природе. Сама форма земли – эллипсоид, или же тор, образованный из эллипса. Открытый тор тоже можно встретить в природе – кольца вокруг планет. Это тор, образованный от очень узкого эллипса.