Условия на границе раздела двух диэлектрических сред

С помощью теоремы о циркуляции вектора напряженности E

и теоремы Гаусса для вектора электрического смещения D получим

условия, устанавливающие взаимосвязь между характеристиками электростатического поля на границе двух диэлектриков.

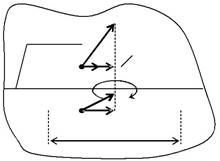
Применим теорему о циркуляции вектора напряженности E по замкнутому контуру L, который вытянут вдоль границы раздела ди-электриков (рис. 2.9.1). Будем стягивать этот контур к границе так, чтобы длина его участков, пересекающих границу, стремилась к нулю.

Граница E2

Контур L

E2

dl

Обход

E1

E1 l

Рис. 2.9.1

В этом предельном случае вклад в циркуляцию будут вносить только

те участки контура, которые параллельны границе. Тогда получим:

E

l E

l 0

E

E

.

(2.9.1)

Edl

L

С учетом формулы (5.20) имеем:

E

E

D

D

D

D

.

(2.9.2)

Теперь запишем теорему Гаусса для замкнутой поверхности S в виде короткого цилиндра (рис. 2.9.2).

	n –нормаль
	D2
D2n		S
		h
D1n	D1
	n
Рис. 2.9.2

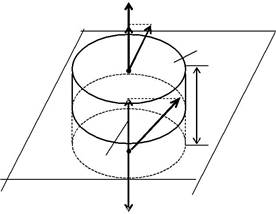
При уменьшении высоты цилиндра ( h 0) поток вектора

электрического смещения D через замкнутую поверхность S будет определяться только потоком через верхнее и нижнее основания цилиндра.

При отсутствии свободных зарядов на границе диэлектриков (q = = 0) получим:

D_n dS q D_n dS 0

S

S

D2 n S D1n S 0

D2 n D1n.

(2.9.3)

С учетом формулы (5.20) имеем:

D

D

E

2 n

E

2 n

1n

1 0 1n

(2.9.4)

E

2 n

E

.

1n

Таким образом, на границе двух диэлектриков выполняются со-

отношения (2.9.1)–(2.9.4).

Резюмируя, можно сказать, что при переходе через границу раз-дела двух диэлектриков нормальная составляющая вектора электриче-ского смещения D_n и тангенциальная составляющая вектора напря-женности E изменяются непрерывно. Тангенциальная же составляю-щая вектора электрического смещения D и нормальная составляющая вектора напряженности E_n при переходе через границу раздела пре-терпевают разрыв.

Заметим, что при наличии свободных зарядов на границе раздела

	D2n– D1n= ,					(2.9.5)
где – поверхностная плотность свободных зарядов.
Используя граничные условия (2.9.1)–(2.9.4) для векторов	и D,
E
получим закон преломления линий вектора электрического смещения D
(линий вектора напряженности E ).
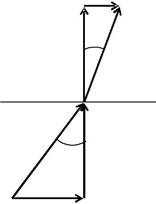
Из рис. 2.9.3 видно, что
tg	D1	и tg			D2	.		(2.9.6)
		D1n			D2n

С учетом формул (2.9.1) и (2.9.3) получаем:

tg 2		D2	D1n	D2	0 2 E2	2 .	(2.9.7)
D
tg		D	D	E
		2 n			0 1 1

^D2

D_2n^{2 D}2

2 1

^D1 ₁ ^D1n

^D1

Рис. 2.9.7

Соотношение (2.9.7) выражает закон преломления линий элек-трического смещения на границе раздела двух диэлектриков.

Лекция № 6

2.10. Сегнетоэлектрики. Диэлектрический гистерезис. Температу-

ра Кюри.

2.11. Эффекты, наблюдаемые в сегнетоэлектриках и других ди-электриках. Применение сегнетоэлектриков в науке и технике.