П.1.2. Цилиндрические координаты

Положение точки М с декартовыми координатами x,y,z в цилиндрических координатах описывается тремя независимыми числами (рис. П.1.):

- расстоянием r (r 0) от оси Oz до точки М (проекцией радиус-вектора точки М на

плоскость xOy);

- углом f ( 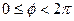) между осью Ох и проекцией 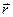на плоскость хОу;

- проекцией z радиус-вектора точки М на ось Оz ( 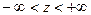).С координатами r, f и z связана тройка ортогональных единичных векторов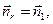 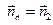и .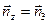

При этом декартовы координаты x, y, z точки М связаны с ее цилиндрическими координатами соотношениями:

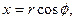
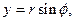
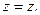
Элементы длины, площади и объема в цилиндрических координатах имеют вид:

,

.

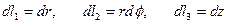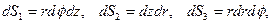
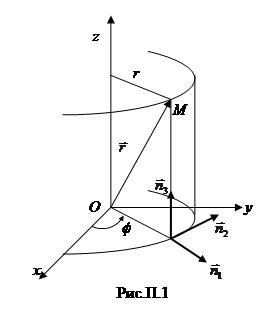
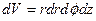Операторы теории поля записываются в цилиндрических координатах следующим образом:

;

;

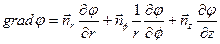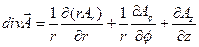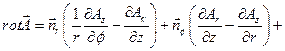
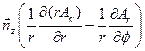
Оператор Лапласа в цилиндрических координатах имеет вид:

,

или 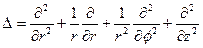.