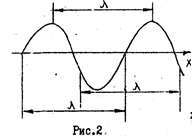
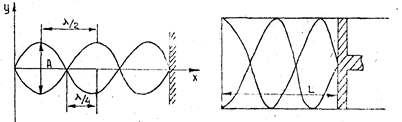Методика определения скорости звука в воздухе.
Возникновение собственных колебаний в столбе воздуха можно использовать для нахождения скорости распространения звука в воздухе. Эту скорость можно определить, зная длину волны λ распространяющейся от источника колебаний с известной частотой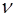 
, по формуле:
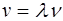(34)
Для измерения длины волны используется экспериментальная установка, состоящая из стеклянной цилиндрической трубы, внутри которой может перемещаться подвижной металлический поршень. На противоположном конце трубы укреплен микрофон, превращающий акустические колебания в электрические (рис. 5).. Последние усиливаются осциллографом, на экране которого можно наблюдать зависимость электрического сигнала от времени. На поверхности трубы имеется узкое отверстие, через которое из динамика в замкнутый объем (резонатор) поступает звуковая волна. В результате дифракции и отражения от стенок трубы в резонаторе образуется несколько типов колебаний. При определенных положениях поршня возникает стоячая волна, аналогичная той, которая возникала бы при падении на поршень плоской волны, распространяющейся вдоль оси трубы (назовем ее осью Х) и отражении от него. Перемещая поршень, можно добиться максимального сигнала в микрофоне. В этом случае положение пучности совпадает с положением мембраны микрофона, а на границе воздух-поршень образуется узел. Если частота фиксирована, то устойчивые колебания устанавливаются только при определенных расстояниях L между поршнем и мембраной, которые, как казалось бы, можно определить из формулы (31).
х2х1х0xmic
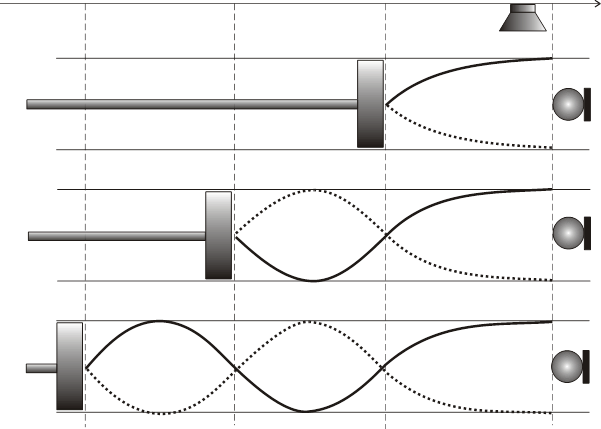
Рис. 5
Однако она справедлива только для идеального случая. Имеется несколько причин, по которым эта формула на практике оказывается весьма неточной.
Во-первых, данная формула соответствуют так называемым идеальным границам: акустическое сопротивление второй среды стремится к бесконечности (закрытая граница) или оно стремится к нулю (открытая граница). Так как акустическое сопротивление второй среды всегда имеет конечное значение, то узлы и пучности смещаются от закрытого и открытого концов трубы. Особенно сильным оказывается смещение пучности от открытого конца трубы. Пучность точно совпадала бы с открытым концом трубы, если бы акустическое сопротивление граничащей среды было равно нулю. Это соответствовало бы границе воздух – вакуум, что совершенно нереализуемо. Более того, в нашем случае на второй границе (в микрофоне) происходит частичное поглощение звука.
Второй причиной, по которой формула (31) оказывается неточной, являются так называемые волноводные эффекты, усиливающиеся по мере роста диаметра трубы.
Наконец, поглощение энергии звуковой волны воздухом также вносит коррективы в указанную формулу.
По указанным причинам формула (31) соответствует только идеальным условиям и на практике точно не выполняется. Однако можно воспользоваться следующим обстоятельством.
Пусть при некотором минимальном значении расстояния между поршнем и микрофоном L=Lmin в нашем резонаторе возникают устойчивые колебания, о чем будет свидетельствовать максимальное значение сигнала в микрофоне (положение пучности совпадает с координатой мембраны xmic). Координату соответствующей границы поршень-воздух (положение узла) обозначим х0. По указанным выше причинам, зависимость амплитуды стоячей волны от пространственной координаты х вдоль оси трубы в интервале между х0и xmic не будет точно описываться формулой (28). Как показывает опыт, в нашем случае, как и в ранее рассмотренном идеализированном, при увеличении длины столба воздуха на величину, равную точно λ/2, снова возникают устойчивые колебания и в микрофоне снова достигается максимум интенсивности. Увеличение длины столба воздуха достигается перемещением отражающей границы (поршня) в направлении от микрофона в новое положение х1. При этом модуль разности х1-х0 (равный разности длин столбов воздуха), с высокой степенью точности равен λ/2.
В пространстве между х1 и х0 образуется обычная стоячая волна, для которой зависимость амплитуды вдоль оси трубы уже хорошо описывается формулой (28). Распределение же амплитуды вдоль оси трубы в промежутке между х0 и xmic будет таким же, как и в первом случае. При достаточно длинной трубе возможно несколько положений поршня, при которых достигается максимум сигнала в микрофоне, и расстояние между любыми такими соседними положениями поршня с высокой степенью точности будет составлять λ/2.
Задание
1. Включить осциллограф. На звуковом генераторе установить значение первой из указанных частот и включить генератор.
2. Перемещая поршень в направлении от микрофона, определить два соседних положения поршня, х0 и х1, при которых достигается максимальное значение сигнала на осциллографе, с которым соединен микрофон. За положение поршня принимается кооордината плоскости поршня, от которой отражается волна (т.е. плоскости, обращенной к микрофону). 
3. Определить скорость звука в воздухе, используя формулу
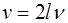, (35)
где 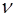- частота колебаний звукового генератора, 
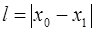- измеренное расстояние между двумя соседними положениями поршня, при которых достигается максимальное значение сигнала на осциллографе (т.е. расстояние между соседними узлами).
4. Повторить пункты 2-3 для двух других частот.
5. Рассчитать абсолютную и относительную погрешности скорости звука.
6. Рассчитать показатель адиабаты для воздуха по формуле (11).
Таблица 1
| Номер измерения | υ= Гц | υ= Гц | υ= Гц | |||||||||
| Х0,м | Х1,м | l,м | Δl,м | Х0,м | Х1 | l | Δl | X0 | X1 | l | Δl | |
| Среднее значение |
Таблица 2
μ, 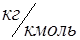 | R,  | Т,К |
Таблица 3
| υ, Гц | Δυ, Гц | 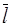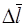 , м |  , м | v, м/c | Δv, м/c | εV | γ | Δγ |
