Система двух линейных уравнений с двумя неизвестными.

ТЕХНИКУМ

(Техникум ФГБОУ ВПО РГУПС)

МЕТОДИЧЕСКИЕ указания

для выполнения самостоятельных,

практических и конторольных работ

для студентов 1 курса очного отделения

по учебной дисциплине ОПД 01 «Математика»

Тема: «Системы линейных алгебраических уравнений»

БАЗОВАЯ Подготовка СПО

Ростов - на - Дону

Рассмотрена Предметной (цикловой) комиссией специальности «Естественно-научных и гуманитарных дисциплин»	Методические указания для выполнения самостоятельных, практических и контрольных работ для студентов 1 курса очного отделения по учебной дисциплины ОПД 01 «Математика» разработаны на основе рабочей программы по специальности 270825, 230401 Строительство железных дорог, путь и путевое хозяйство, Информационные системы (по отраслям)
Председатель:	Заместитель директора по УР

Методические указания для выполнения самостоятельных, практических и контрольных работ для студентов 1 курса очного отделения по учебной дисциплины ОПД 01 «Математика» разработаны на основе рабочей программы по специальности 270825, 230401 Строительство железных дорог, путь и путевое хозяйство, Информационные системы (по отраслям)

Разработчик:

В. В. Абрамов, преподаватель математики техникума ФГБОУ ВПО РГУПС.

Рекомендована объединенной методической комиссией техникума ФГБОУ ВПО РГУПС.

Заключение ОМК № ________ от «____» _____________20__г.

Содержание

	стр
Пояснительная записка
1 Системы двух линейных уравнений с двумя неизвестными
2 Анализ формул Крамера
3 Определители второго порядка
4 Свойства определителей второго порядка
5 Определители третьего порядка
6 Свойства определителей третьего порядка
7 Метод Крамера для СЛАУ третьего порядка
8.1 Решение СЛАУ методом Гаусса
8.2 Правило равносильных преобразований систем
8.3 Метод Гаусса
9 Решение систем двух уравнений с двумя неизвестными, когда одно линейное, а другое – второй степени
10 Практические задания
11 Список рекомендованной литературы

Пояснительная записка

«Если вы хотите научиться плавать,

То смело входите в воду, а если хотите

научиться решать задачи, то решайте их!»

Д. Пойа

Цель данного методического пособия дать необходимые навыки работы с системами линейных алгебраических уравнений и систем двух уравнений с линейным и квадратичным уравнением. Несмотря на простоту данной темы, она находит большое применение в реальной математике. Так зачастую, решая интегральные уравнения методом коллокаций, вопрос о нахождении решения этого интегрального уравнения, сводится к нахождению решения некоторой системы линейных алгебраических уравнений.

В школьном курсе нам были известны два основных метода решения систем линейных алгебраических уравнений: метод сложения и метод подстановки. На их основе в данном методическом пособии, мы постараемся развить новые методы решения систем линейных алгебраических уравнений. Для этой цели будут введены, хотя и не строго, такие понятия как определитель второго и третьего порядков, правило равносильных преобразований систем линейных алгебраических уравнений. Говоря о не строгости введения этих понятий, стоит отметить, что для реальной жизни и простоты понимания излагаемого материала, такого рода изложения вполне достаточно. Более того, по мнению автора, предложенный здесь материал может послужить одной из первых ступеней для дальнейшего изучения этой темы, но уже в разрезе фундаментальной математики.

Так же, неким дополнением к основному материалу этого пособия, служит материал, посвященный решению систем двух алгебраических уравнений с двумя неизвестными, в которых одно из уравнений линейное, а второе квадратичное.

Методическое пособие содержит много практических примеров для самостоятельной работы, но внимательный читатель заметит и несколько теоретических заданий. Для полного понимания данного в пособии материала рекомендуем решать как практические упражнения, так и доказывать теоретические задания. Это поможет освоить, более основательно темы, изложенные ниже. Придерживаясь цитаты введенной выше, автор полагает, что студент, заинтересованный в изучении материала, должен проделать большую самостоятельную работу, нацеленную на получение устойчивого практического навыка по решению систем линейных алгебраических уравнений и нахождению определителей второго и третьего порядков.

При изучении тем изложенных ниже, читатель может столкнуться с некоторыми непонятными ему обозначениями. Поэтому перечислим часто встречающиеся обозначения, которые могут вызвать трудности, и желаем удачи в изучении материала.

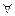- для любого, каждого.

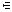- принадлежит, находится в,

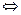- равносильно,

~ - эквивалентно,

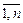- все натуральные числа от 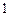до ,

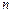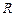- множество вещественных чисел.

Система двух линейных уравнений с двумя неизвестными.

Определение №1.1: Выражение вида 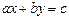называется линейным уравнением с двумя неизвестными, где 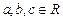называемые коэффициентами этого уравнения, а 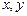– искомые неизвестные. Коэффициент 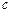называется правой частью или свободным членом.

Определение №1.2: Выражение вида:

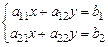(1.1)

называется Системой двух линейных алгебраических уравнений (СЛАУ).

Замечание №1.1: Если 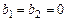, то система (1) называется однородной системой линейных уравнений (ОСЛУ).

Определение №1.3: Упорядоченная пара чисел 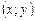, при подстановке которых в СЛАУ (1.1) приводит каждое из уравнений системы к верному числовому равенству, называется решением данной СЛАУ.

Рассмотрим СЛАУ

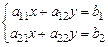(1.2)

Очевидно, что если коэффициенты этой СЛАУ 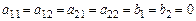, то любая пара чисел 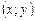– решение данной СЛАУ (1.2). Если же 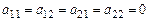и 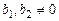, то СЛАУ (1.2) не имеет решений.

Определение №1.4:Если СЛАУ имеет хотя бы одно решение, то она называется совместной, в противном случае СЛАУ называется несовместной.

Далее, будем рассматривать такие СЛАУ, где хотя бы один из коэффициентов 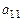, , 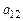, 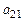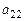не равен нулю. Пусть 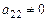, тогда

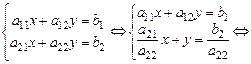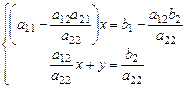(1.3) (1.4)

В этом случаи, если 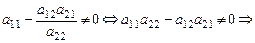из (1.3) и (1.4)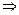

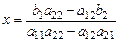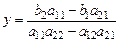(1.5) (1.6)

Если обозначить через 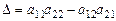, , 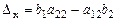, 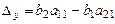то формулы (1.5) и (1.6) перепишется как:

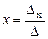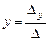(1.7) (1.8)

Формулы (1.7) и (1.8) носят название формул Крамера.

Пример №1.2

Найти решение системы двух линейных уравнений методом Крамера

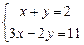
Решение:

Воспользуемся формулами Крамера. Для этого найдем 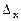, 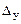и 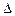. Из СЛАУ видно, что 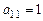, , 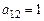, , 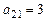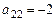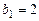и 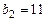. Тогда по формулам (1.7) и (1.8) следует:

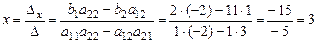
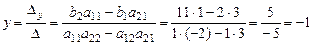
Ответ: , .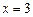

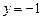Анализ формул Крамера.

Рассмотрим подробней вопрос о существовании и количестве решений СЛАУ второго порядка.

1) Если 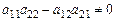, то система (1.2) имеет единственное решение (1.5) и (1.6). То есть, если 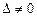, то система (1.2) имеет единственное решение, которое ищется по формулам Крамера (1.7) и (1.8).

2) Если 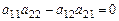, то (1.2) примет вид:

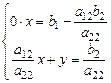(2.1)

Тогда возможны следующих два варианта:

А) Если 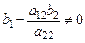, то система (2.1) не имеет решений, то есть является несовместной.

Б) Если 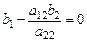, то система (5) имеет бесконечно много решений. Действительно, положим 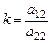, тогда из (1.3) и (1.4) получим, что 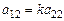и 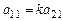. С учетом сделанного предположения (2.1) перепишется:

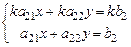
Таким образом, если 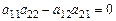, то первое уравнение СЛАУ получается из второго уравнения, путем умножения второго уравнения на коэффициент 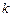. В этом случаи СЛАУ (2.1) имеет бесконечно много решений.

Вывод: Если 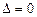, то система (2.1) имеет или бесконечно много решений, или вовсе их не имеет.

Рассмотрим частный случай СЛАУ - ОСЛУ:

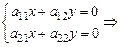
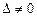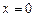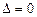Если , то эта система всегда имеет решение и . Если же и 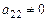, то решением этой системы будет любая пара чисел 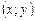, такая что , .

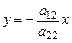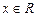Вывод: ОСЛУ всегда совместно.