Моделирование цифровой следящей системы
Соберем в системе Matlab Simulink следующую схему:

Рис. 9. Схема набора цифровой следящей системы в пакете Matlab Simulink
Данная схема содержит последовательно включенные непрерывные звенья, соответствующие заданной системе, и дискретное передаточное звено, соответствующее дискретной передаточной функции корректирующего звена, найденной в п. 2.2.
Для правильного моделирования цифровой следящей системы необходимо в свойствах блока Discrete Transfer Fcn параметр Sample Time задать равным 0,01 (т.е. периоду квантования по времени, выбранному в п. 2.6), а также в параметрах симуляции указать переменный шаг (Variable-step) типа ode45 (Dormand-Prince). В результате проведения моделирования получим следующий график переходного процесса:
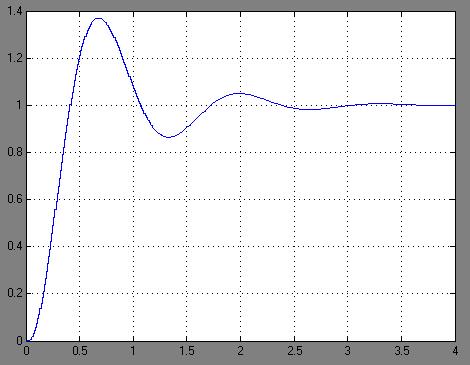
Рис. 10. График переходного процесса цифровой следящей системы
Как видно, данный график практически идентичен графику скорректированной системы, представленному на рис. 8. Также параметры качества переходного процесса цифровой следящей системы следующие:
максимальное перерегулирование σmax=27.002%;
время регулирования tp=1.6c.
Эти показатели качества практически полностью идентичны показателям качества скорректированной системы, найденным в п. 3.2. Можно сделать вывод, что дискретная передаточная функция корректирующего звена найдена правильно.
Разработка принципиальной схемы цифровой следящей системы
На принципиальной схеме должны быть изображены сельсин-датчик и сельсин-трансформатор, фазовый детектор, АЦП, цифровой вычислитель, ЦАП, электронный усилитель мощности, ЭМУ, двигатель, редуктор.
Схема приведена в приложении
Заключение
В ходе данной курсовой работы была резработана следящая система, которая удовлетворяет определенным техническим условиям. Система обеспечивает синхронное исифазное вращение двух осей, механически не связаных между собой. Входом системы является угол поворота сельсина-датчика, а выходом – угол поворота выходного вала редуктора, механически связанного с рабочим механизмом и с ротором сельсина-приемника.
Для обеспечения заданных показателей качества переходного процесса в систему вводится цифровое управляющее звено. Расчет корректирующего звена проводится методом логарифмических частотных характеристик, разработанным для расчета непрерывной системы управления. Использование данного метода для расчета цифрового корректирующего звена основано на предположении о том, что при малом периоде квантования по времени цифровая система по своим свойствам приближается к непрерывной, а при достаточно большом числе цифровых разрядов вычислительного устройства нелинейностью, вносимой квантованием сигналов по уровню, можно пренебречь.
Следущие системы рассматриваемого типа широко применяются для дистанционного управления различными механизмами, а также при построении автоматических систнм управления в различных отраслях промышленности.
