Определение угла наклона плоскости к плоскости проекций.
Конспект лекций
Лекция №3
Лектор потока: Зелёв Александр Павлович (доцент кафедры начертательной геометрии и черчения).
2.6 Проекционные свойства прямого угла
| Теорема о проецировании прямого угла (прямая) Если одна сторона прямого угла параллельна плоскости проекций, а другая сторона угла не перпендикулярна плоскости проекций, то на данную плоскость проекций угол проецируется без искажения. Ситуация показана на изображении: | |
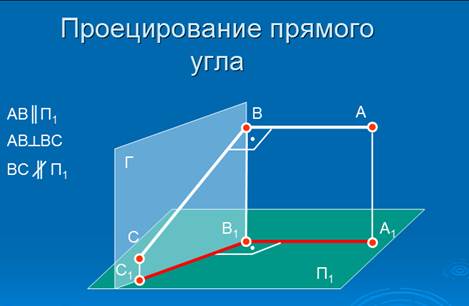 | |
| Практическое применение находит обратная теорема при изучении свойств угла по комплексному чертежу. Теорема о проецировании прямого угла (обратная): если одна сторона некоторого угла параллельна плоскости проекций и на эту же плоскость проекций угол спроецировался в прямой угол, то данный угол также является прямым. Рассмотрим пример: | |
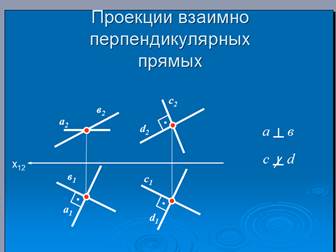 | В примере прямая а параллельна плоскости проекций П1, и на П1 угол спроецировался в прямой угол. Поэтому прямые а и b взаимно перпендикулярны. Прямые с и d не параллельны ни к одной из плоскостей проекций. Поэтому здесь не действует теорема о проецировании прямого угла. В общем случае угол спроецировался с искажением. То есть, данные прямые не взаимно перпендикулярны. |
Проекции плоскостей
Определение угла наклона плоскости к плоскости проекций.
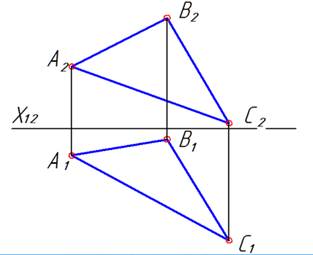
Постановка задачи. Дана плоскость общего положения Г. Требуется определить углы наклона плоскости Г к плоскостям проекций (отдельно к плоскости П1, к плоскости П2, к плоскости П3).
Пусть плоскость задана треугольником Г(АВС):
 | |
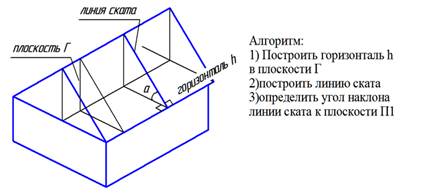
| Для изучения алгоритма рассмотрим известный геометрический объект – плоскость крыши дома. В этой плоскости построим горизонталь (кромка крыши). Построим еще одну прямую – линию ската, по которой скатывается материальная точка. Линия ската – прямая, принадлежащая исследуемой плоскости общего положения и принадлежащая данной плоскости. Из школьной программы: углом между двумя плоскостями является угол между прямыми в данных плоскостях, перпендикулярными к линии пересечения. В рассматриваемом случае проведем через горизонталь плоскость уровня, параллельную П1. Тогда углом между плоскостью крыши и горизонтальной плоскостью будет угол между линией ската и ее горизонтальной проекцией. | |
 | |
| Возвращаемся к комплексному чертежу. По этому алгоритму через любую точку плоскости Г построим горизонталь в плоскости Г. Например, через точку А. Построение начинаем с фронтальной проекции (горизонталь параллельна П1) | 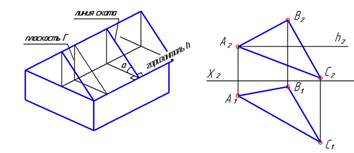 |
| «Привязываем» ее к плоскости Г с помощью точки на ВС. | 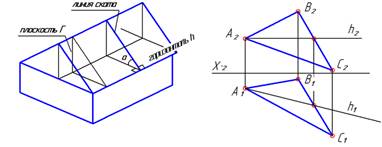 |
| Строим проекции линии ската. Таких линий – бесчисленное множество. Построим, например, через точку В. Используем проекционные свойства прямого угла. Так как линия ската перпендикулярна горизонтали, то на П1 линия ската m1 должна быть перпендикулярна h1. | 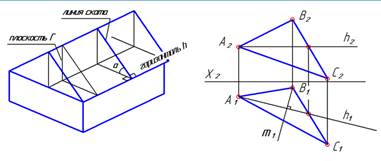 |
| Линия ската принадлежит плоскости Г. Поэтому ее «привязываем» к плоскости Г с помощью точек этой плоскости. Здесь применили точки В и К. Таким образом, построили две проекции линии ската m. | 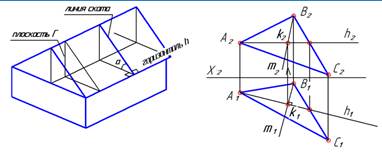 |
| Далее, надо определить угол наклона линии ската m к плоскости проекций П1. Возьмем любой отрезок на линии ската и с помощью способа прямоугольного треугольника определим этот угол. Для удобства построения используем отрезок ВК, так как в точке К уже построен прямой угол. Искомый угол – угол a. | 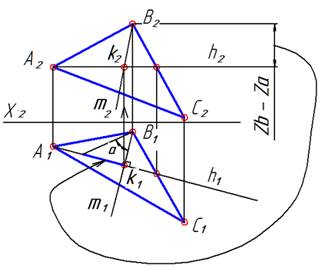 |
| Для построения угла наклона плоскости Г к плоскости проекций П2 используем фронталь. |
