Уравнение гармонических колебаний

Наиболее распространены гармонические колебания, то есть колебания, подчиняющиеся закону синуса или косинуса. Это происходит, как будет показано далее, если возвращающая сила пропорциональна смещению. Пусть координата тела изменяется в зависимости от времени по закону

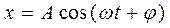. (14.1)

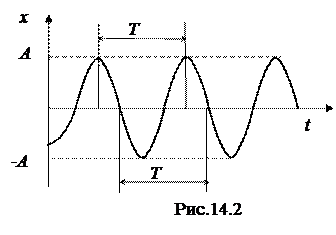
Здесь А – амплитуда колебаний, то есть наибольшее смещение тела от положения равновесия, ω – циклическая частота, равная числу колебаний за 2π секунд. Аргумент косинуса называется фазой, φ – начальной фазой колебаний.

Процесс колебаний характеризуются периодом колебаний 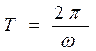(рис. 14.2). Это время одного полного колебания, за которое фаза колебаний возрастает на 2π радиан. Кроме того, используется понятие частоты 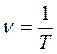, которая равна числу колебаний в единицу времени.

Скорость и ускорение при гармонических колебаниях определим как производные от уравнения координаты

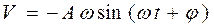, (14.2)

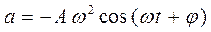. (14.3)

Из вида уравнений видно, что скорость и ускорение также изменяются со временем по гармоническим законам. Ускорение всегда направлено в сторону, противоположную смещению, то есть, всегда направлено к положению равновесия. Ускорение максимально в крайней точке траектории, при х=А, и равно 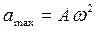. Максимальная скорость достигается телом при x = 0, в момент прохождения положения равновесия и равна .

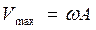Механическая энергия колебаний равна сумме кинетической и потенциальной энергий

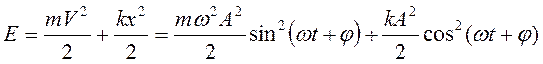. (14.4)

При прохождении маятником положения равновесия кинетическая энергия достигает максимального значения, а потенциальная энергия становится равной нулю. Через четверть периода в крайнем положении максимального значения достигает потенциальная энергия, а кинетическая энергия становится равной нулю. По закону сохранения механической энергии полная энергия свободных колебаний постоянна

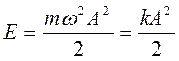. (14.5)

Пружинный маятник

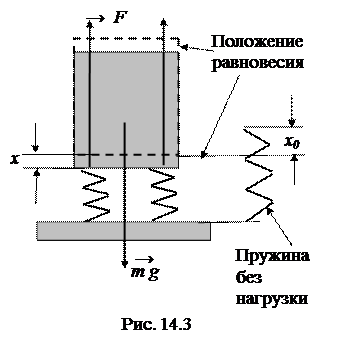
Рассмотрим колебания пружинного маятника на примере вертикальных колебаний вагона. Пусть вагон, опирающийся на пружины подвески, выведен из положения равновесия в вертикальномнаправлении и отпущен. Под действием сил упругости он начнет смещаться обратно к положению равновесия, увеличивая скорость движения. В положении равновесия он не остановится, а по инерции продолжит движение, пока сила упругости не остановит его. Потом движение под действием упругой силы повторится в обратном направлении, и возникнут собственные колебания вагона.

x

Когда вагон находится в равновесии, то сила тяжести вагона компенсируется силой упругости пружин mg = kx₀ (рис. 14.3). Здесь
х₀ – деформация первоначально свободных пружин под действием силы тяжести вагона, 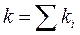– суммарный коэффициент упругости всех пружин подвески, соединенных параллельно. При смещении вагона в процессе колебаний относительно положения равновесия на расстояние х результирующая сила, действующая на вагон, будет равна F = – k (x₀ +x) + mg = – k x. То есть сила тяжести вагона, скомпенсированная силой упругости предварительного сжатия пружин, на процесс колебаний не влияет.

Определим период свободных колебаний кузова вагона. Запишем уравнение второго закона Ньютона для смещения вагона под действием возвращающей силы упругости пружин подвески F= – kx

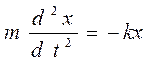. (14.6)

Здесь ускорение записано как вторая производная от координаты по времени. Уравнение (14.4) – это дифференциальное уравнение второго порядка. Решением уравнения является функция, превращающая его в тождество. То есть эта функция и ее вторая производная должны иметь одинаковую зависимость от времени, но разного знака. В математике такими функциями являются функция синуса и косинуса и экспонента с мнимым показателем.

Ищем решение в виде гармонической функции x = A cos ωt. Вторая производная функции равна 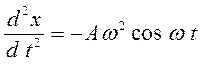. Подставив искомое решение в дифференциальное уравнение второго закона Ньютона, убедимся, что оно превращается в тождество при условии, если циклическая частота колебаний равна 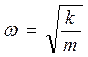. Соответственно, период вертикальных свободных колебаний будет равен

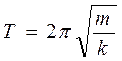. (14.7)

Период свободных вертикальных колебаний не зависит от амплитуды колебаний вагона. Период возрастает при увеличении массы вагона (например, при погрузке) и при уменьшении упругости пружин. Для пассажирских вагонов, с целью обеспечения комфорта пассажирам, упругость пружин подвески выбирается, сравнительно с грузовыми вагонами, небольшой, так чтобы частота собственных колебаний была бы около 2 Гц, при которой пассажир испытывает сонливость.

Амплитуда свободных колебаний А определяется энергией Е, сообщенной внешним воздействиям в начале при возбуждении колебаний. Энергия колебаний равна максимальному значению потенциальной энергии 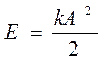. Откуда амплитуда колебаний равна

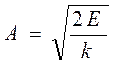. (14.8)

При вертикальных колебаниях вагона сила давления колес на рельсы из постоянной, равной силе тяжести вагона, превратится в пульсирующую по величине силу. Добавочная сила будет равна силе инерции F=ma или равной ей силе упругости пружин подвески F=kx,

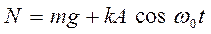. (14.9)

Периодическая нагрузка на колеса, рельсы, кузов вагона отрицательно влияет на вагоны, выводит их из строя раньше, чем постоянное воздействие даже большей величины силы. Колебания ухудшают сцепление колеса с рельсом. В момент минимального давления, может происходить частичное буксование, сход колеса с рельса. Поэтому возникшие колебания следует гасить с помощью амортизаторов.

Физический маятник

Физический маятник – это тело произвольной формы, точка подвеса которого расположена выше центра тяжести. Если в поле тяжести маятник отклонить от положения равновесия и отпустить, то под действием силы тяжести маятник стремится к положению равновесия, но, достигнув его, по инерции продолжает движение и отклоняется в противоположную сторону. Затем процесс движения повторяется в обратном направлении. В итоге маятник будет совершать вращательные собственные колебания.

Для вывода формулы периода собственных колебаний маятника применим основной закон динамики вращательного движения: угловое ускорение тела прямо пропорционально моменту силы и обратно пропорционально моменту инерции тела относительно оси вращения:

e = 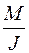. (14.10)

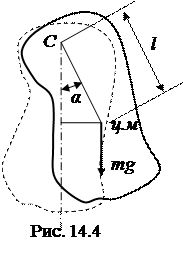
Момент силы по определению равен произведению силы на плечо силы. Плечо силы – это длина перпендикуляра, опущенного из оси вращения на линию действия силы. Для маятника плечо силы тяжести равно d = lsin a, где l – расстояние между осью вращения C и центром тяжести ц.м. маятника (рис. 14.4). При малых колебаниях маятника угол отклонения a сравнительно мал, а синусы малых углов с достаточной точностью равны самим углам. Тогда момент силы тяжести можно определить по формуле М=−mgl∙a. Знак минус обусловлен тем, что момент силы тяжести противодействует отклонению маятника. Так как угловое ускорение – это вторая производная от угла поворота по времени, то основной закон динамики вращательного движения (14.10) принимает вид

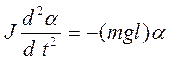. (14.11)

Это дифференциальное уравнение второго порядка. Его решением должна быть функция, превращающая уравнение в тождество. Такой функцией может быть функция косинуса или синуса

a = a₀sin(w t + j ). (14.12)

При подстановке решения (14.12) в дифференциальное уравнение (14.11), после сокращения, получим, что уравнение превращается в тождество, если циклическая частота колебаний равна 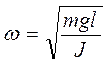. Циклическая частота связана с периодом колебаний соотношением T = 2p /w. Отсюда

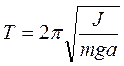. (14.13)

Эта формула позволяет экспериментально определять моменты инерции тел, если их представить физическим маятником, по измеренному периоду колебаний.