Список используемых источников. (экзамен, контрольная работа)

Высшая математика

III семестр

(экзамен, контрольная работа)

Тема 1 Комплексные числа

Тема 2 Функция комплексного переменного

Тема 3 Производная функции комплексного переменного

Тема 4 Интеграл функции комплексного переменного

Тема 5 Ряд Тейлора, Лорана

Тема 6 Преобразование Лапласа

Тема 7 Операционное исчисление

Тема 8 Приложения операционного исчисления

Формирование исходных данных к задачам

Условия задач, входящих в контрольную работу одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.

Для того, чтобы получить личные числовые данные, необходимо взять две последние цифры своего шифра (А – предпоследняя цифра, В – последняя) и выбрать из таблицы 1 параметр m, а из таблицы 2 параметр n. Эти два числа m и n и нужно подставить в условия задач контрольной работы.

Таблица 1 (выбор параметра m)

А
m

Таблица 2 (выбор параметра n)

В
n

Например, если шифр студента 22037, то А=3, В=7, и из таблиц находим, что m=1, n=5. Полученные m=1 и n=5 подставляются в условия всех задач контрольной работы этого студента.

Функции комплексного переменного

1.1. Действия с комплексными числами.

Выполнить действия:

а) (т+iп)² (n-im); b)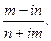

1.2. Решить уравнение:

z²-i (m +n) z-mn-1+i(n-m)=0

Аналитические функции.

2.1. Показать, что функция f(z)=(z+m)²+z-ni аналитична.

2.2. Найти производную функции f(z)=e^mz +cos(nz) в точке z_o= 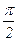i.

Интегрирование функций комплексного переменного.

3.1. Вычислить 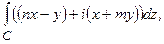где контур С- незамкнутая ломанная,соединяющая точки 0(0,0), A(m,n) u B(0,m+n).

Ряды Тейлора, Лорана и Фурье.

4.1. Разложить функцию f(z)=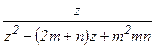

в окрестности точки z₀ в ряд Тейлора и найти радиус сходимости ряда.

4.2. Разложить функцию f(z)= 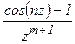в окрестности точки z₀ = 0 в ряд Лорана.

Вычеты и их приложения.

5.1. Определить тип особых точек функции f(z)= 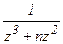и найти вычеты в них.

5.2. Вычислить с помощью вычетов .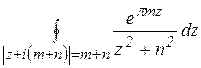

Операционное исчисление.

6.1. Нахождение изображений и восстановление оригиналов.

6.1.1. Найти изображения функций:

а) f(t)= 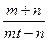; б) f(t)=cos²(mt)+tּsin(nt).

6.1.2. Восстановить оригиналы по изображениям:

а) F(p)= 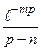; б) F(p)= .

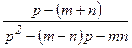6.2. Приложения операционного исчисления.

Решить операционным методом дифференциальное уравнение:

a) 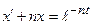, x(0)=m;

б) 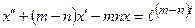, x(0)=0,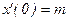

Вопросы к экзамену

1.Комплексные числа, действия с комплексными числами

2 Функция комплексного переменного

3 Производная функции комплексного переменного

4 Интеграл функции комплексного переменного

5 Ряд Тейлора, Лорана

6 Вычеты аналитической функции

7 Оригиналы и изображения

8 Приложения операционного исчисления

Список используемых источников

1. П.Е.Данко, А.Г.Попов, Т.Я. Кожевникова. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 2005. Том2.

2. Н.С.Пискунов. Дифференциальное и интегральное исчисления. – М.: Наука, 1978. Том2.

3. Я.С.Бугров, С.М.Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного – М.: Наука, 2000.

4. М.Л.Краснов, А.И. Кисилев, Г.Н.Макаренко. Функции комплексного переменного. Операционное исчисление. Теория Устойчивости. – М.: Наука, 1981.