Рационал функцияларды интегралдау

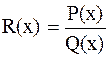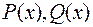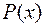1. Қарапайым бөлшектерді интегралдау. Бөлшек рационал функция деп мына түрдегі функцияны айтамыз: , мұндағы коэффициенттері нақты болып келген көпмүшеліктер. Егер рационал бөлшектің алымында тұрған көпмүшесінің дәрежесі, оның бөліміндегі көпмүшесінің дәрежесінен кем болса, оны дұрыс рационал бөлшек деп атайды, ал керісінше жағдайда бұрыс рационал бөлшек деп атайды. Кез келген дұрыс рационал бөлшек келесі төрт түрлі қарапайым бөлшек функциялардың қосындысына жіктелуі мүмкін:

1) ,

2) ( 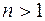-натурал сандар),

3) ,

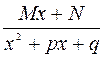4) 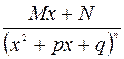( 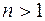-натурал сандар),

мұндағы 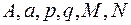-нақты сандар, ал - нақты түбірі жоқ үшмүшелік, яғни .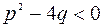

Жоғарыдағы бастапқы үш қарапайым бөлшектерді интегралдау оңай болғандықтан, олардың интегралын тікелей жазамыз:

1)

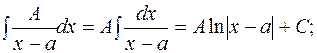
2)

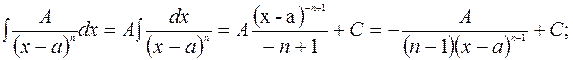
3)

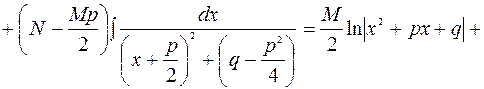
4) 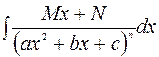түріндегі интеграл келесі түрде табылады:

Квадраттық үшмүшелікті түрлендіреміз және мынадай ауыстыру енгіземіз . Сонда

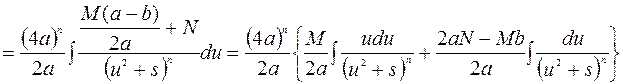
Соңғы теңдікте бірінші интеграл 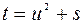ауыстыру арқылы мынадай кестелік интегралға алып келеді , ал екінші келесі (6)-ші реккуренттік формула арқылы алынады:

(6)

Мысал-8.

.

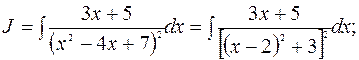
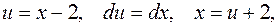
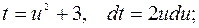
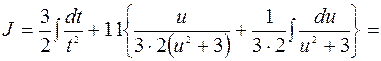
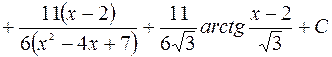2. Рационал бөлшектерді интегралдау. 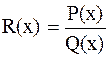, мұндағы 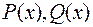коэффициенттері нақты болып келген көпмүшеліктер. Осы рационал өрнегін интегралдау үшін бірінен соң бірі орындалатын үш қадам жасалынады.

Бірінші қадам. Егер бөлшегі бұрыс бөлшек, яғни 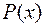көпмүшелігінің дәреже көрсеткіші бөлімінің дәреже көрсеткішінен артық не тең болса, онда 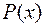көпмүшелігін көпмүшелігіне бөлу арқылы бөлшегінің бүтін бөлігі ажыратылады. Сонда берілген рационал бөлшекті оның бүтін бөлігі және 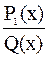дұрыс бөлшегінің қосындысы түрінде жазуға болады:

.

Екінші қадам. 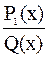дұрыс бөлшегі қарапайым бөлшектерге жіктелінеді. Ол үшін көпмүшелігінің түбірлері табылып оны нақты коэффициентті бірінші және екінші дәрежелі көбейткіштерге жіктейміз:

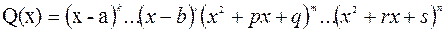(7)

Бөлшектің бөлімі көпмүшелігінің бұл жіктелуіндегі бірінші дәрежелі көбейткіштер көпмүшеліктің нақты түбірлеріне, ал екінші дәрежелі көбейткіштер оның түйіндес жорамал түбірлері жұбына сәйкес келеді. көпмүшелігінде х-тың ең үлкен дәреженің коэффициенті бірге тең деп есептелінеді. Егер ондай болмаған жағдайда 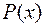және көпмүшеліктерін сол коэффициентке бөліп жібереді.

Осындай түрлендірулер жүргізілгеннен дұрыс бөлшек мынадай формула бойынша қарапайым бөлшектерге жіктеледі.

(8)

мұндағы анықталмаған белгісіз коэффициенттер. Олардың кейбіреулері нөлге тең болып қалуы да мүмкін. Анықталмаған коэффициенттерді табу үшін барлық қарапайым бөлшектер ортақ бөліміне келтіреді де (8) теңдігінің екі жағының алымдарын теңестіреді. Одан соң теңдіктің оң жағы мен сол жағындағы бірдей дәрежелі х-тің коэффициенттері теңестіріліп теңдеулер жүйесі құрылады. Осы теңдеулер жүйесін шешу арқылы біз іздеп отырған коэффициенттерді табамыз.

Үшінші қадам. Берілген бөлшектің бүтін бөлігін және қарапайым бөлшектерін барлығының интегралдары есептелініп, олардың қосындысы табылады. Сонымен рационал бөлшектерді интегралдау көпмүшеліктердің және қарапайым бөлшектердің интегралдарын табуға келіп тіреледі екен.

1-жағдай. Бөлшектің бөлімінің әр түрлі нақты түбірлері бар, яғни көпмүшелік қайталанбайтын бірінші дәрежелі көбейткіштердің көбейтіндісі түрінде жіктеледі.

Мысал-5. Интегралдарды есептеу керек.

1)

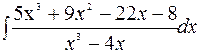
Шешу. 1) Интеграл таңбасының астындағы рационал бөлшек бұрыс, себебі алымының дәрежесі тең. Сондықтан оның бүтін бөлігін ажыратамыз:

Сонда, болады. Дұрыс қалдық бөлшектің бөлімі көбейткіштерге мына түрде жіктеледі

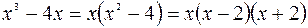
(4) формула бойынша бөлшектің бөліміндегі әрбір жіктелуі не 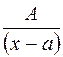түріндегі қарапайым бөлшектер жіктелуінің қосындысы сәйкес келеді. Сондықтан, 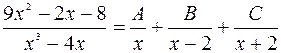. Мұндағы А,В,С – коэффициенттері әзірше бізге белгісіз болғандықтан оларды анықтау қажет. Ол үшін теңдіктің екі жағын да ортақ бөлімге келтіріп, алымдарын теңестіреміз. Мұның нәтижесінде мына тепе-теңдікке келеміз:

.

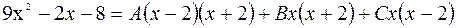Бұл тепе-теңдіктің сол жағы мен оң жағындағы х-тің бірдей дәрежелерінің коэффициенттерін теңестіріп, А,В,С-белгісіздері құрамына кіретін үш теңдеуден тұратын жүйе пайда болады, яғни:

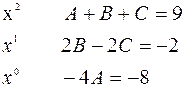
Жүйені шешсек, 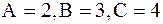болады. Коэффициенттердің мәндерін орындарына қойғанда:

.

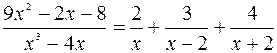Интегралдағанда:

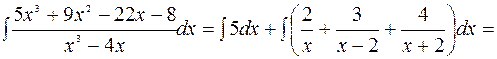
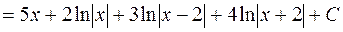
болып шығады.

Жіктеу коэффициенттерін анықтаудың жоғарыда келтірілген әдісі анықталмаған коэффициенттер әдісі деп аталады. Оның мағынасы былай: егер бөлшекті жай бөлшектерге жіктеудің түрі белгілі, бірақ коэффициенттердің өздері белгісіз болса, әуелі олардың орнына әріптік коэффициенттерді жазамыз да, сонан кейін сызықты теңдеулер жүйесінен олардың сандық мәндерін анықтаймыз.

Берілген мысалда А,В,С коэффициенттерін тезірек табуға болатын еді. Шынында: (5) тепе-теңдігіне 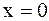десек, оң жақтағы қосылғыштардың біріншісінен басқасы жойылар еді де, бірден 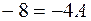теңдігі шығып, онан болып анықталады. Онан соң тізбектей 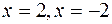деп жорып, жаңағы сияқты 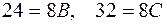, демек 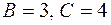болатынын табамыз.

Коэффициенттерді бұлайша анықтау тәсілін әдетте дербес мәндес әдісі деп атайды. Бұл тәсілді қолдану уақытты үнемдеуге мүмкіндік береді, демек, рационал бөлшектерді интегралдауға оған ерекше көңіл бөлген жөн. Бөлшектің бөліміндегі көпмүшеліктің түбірлері тек қана нақты түбірлер болып келген жағдайда белгісіз коэффициенттерді анықтау үшін тек осы әдісті ғана қолдану ыңғайлы. Қалған жағдайда белгісіз коэффициенттерді анықтау үшін екі тәсілді (дербес мәндес және анықталмаған коэффициенттер тәсілін) біріктіре қолдануға болады. Мұның қалай іске асырылатынын төмендегі мысалдар арқылы көрсетелік.

2 жағдай. Бөлшектің бөлімінің нақты түбірлері бар, бірақ олардың кейбіреулері еселі, яғни бөлшектің бөлімі сызықтық көбейткішке жіктеледі де, олардың кейбіреулері қайталанып келеді.

Мысал-6. Интегралдарды есептеу керек.

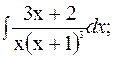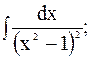1) 2) 3) .

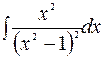Шешуі: 1) Интеграл астындағы бөлшек дұрыс. Оның бөлімі көбейткіштерге жіктелінген, яғни (7) түрінде беріліп тұр. (8) формулаға сәйкес бөлшектің бөліміндегі х көбейткішіне 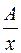, ал 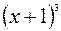көбейткішіне қарапайым үш бөлшектің қосындысы сәйкес келеді: . Сондықтан, интеграл таңбасы астындағы функция мына түрдегі қарапайым бөлшектерге жіктеледі

.

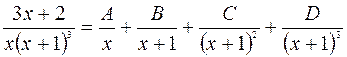Теңдіктің оң жағын ортақ бөлімге келтіріп, оның алымын, сол жағының алымымен теңестіреміз.

.

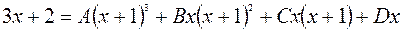Алғаш рет қарағанда бұл тепе-теңдіктің сол жағы мен оң жағындағы х-тердің дәреже көрсеткіштердің сәйкес келмеуі оқушыны таңдандыру мүмкін. Бұл сәйкессіздіктің мағынасы мынада: тепе-теңдіктің сол жағындағы пен 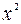- тың коэффициенттерін нольге теңеу қажет. Коэффициенттерді анықтау үшін комбинацияланған тәсілді қолданамыз. Әуелі 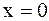, сонан кейін 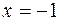деп алсақ, сәйкесінше мен теңдіктері шығады да, олардан 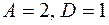болады. Енді пен 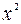- тың коэффициенттерін салыстырсақ, мына теңдіктер шығады:

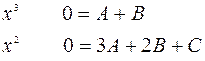
Мұндағы А мен В-нің орындарына олардың сандық мәндерін апарып қойсақ, 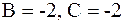болып шағады.

.

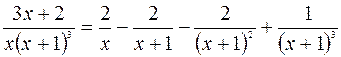Сонда ізделініп отырған интеграл былай табылады:

.