Принцип управления по отклонению (Принцип Ползунова-Уатта)
Систему управления можно построить так, что управляющее воздействие будет вырабатываться на основании информации о выходной величине, т.е. путем сравнения в управляющем устройстве действительного значения управляемой величины с требуемым значением и управлять объектом в зависимости от результатов сравнения. Этот принцип управления называют принципом управления по отклонению или принципом обратной связи.
Такую систему можно получить, если на рисунке 1.4 замкнуть контакты «3-4». Функциональная схема, соответствующая этому случаю, представлена на рисунке 1.6. В этом случае на выходе операционного усилителя сравниваются две величины - напряжение задания Uвх и напряжение Uн, пропорциональное напряжению выходной величины Uг. Очевидно, что установлена связь между управляемой величиной Uг и управляющим воздействием Uвх.
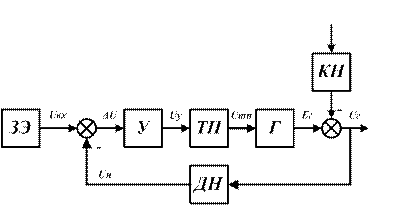
Рисунок 1.6 Функциональная схема замкнутой САУ
У - усилитель; ТП - тиристорный преобразователь; Г - генератор;
ДН - датчик напряжения
Таким образом, характерной чертой систем, построенных на основе принципа управления по отклонению, является наличие обратной связи.
Обратная связь - это такая связь, при которой информация о состоянии управляемого объекта (величина, соответствующая действительному значению выходной величины) передается с выхода системы на вход управляющего устройства. Обратную связь называют отрицательной, если в управляющем устройстве с помощью элемента сравнения (сумматора) определяется отклонение 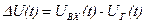 .
.
Принцип управления по отклонению является универсальным и эффективным, поскольку он позволяет управлять неустойчивыми объектами, а также осуществлять требуемый закон изменения управляемой величины с допустимо малым отклонением (ошибкой) DU независимо от того, какими причинами последнее вызвано.
Принцип обратной связи характерен не только для технических систем, но и для живых организмов. Так, например, человек управляет своими действиями, используя в основном принцип обратной связи. К примеру, при перемещении какого-либо предмета устанавливается связь между положением этого предмета и сокращением соответствующих мышц, необходимых для его перемещения. Существование живых организмов и природы немыслимо без наличия обратных связей.
В случае разомкнутой системы (контакты «1-2» и «3-4» разомкнуты, рисунок 1.4, 1.5) напряжение генератора изменяется под воздействием целого ряда внешних и внутренних факторов: изменения тока нагрузки Iн при изменении сопротивления Zн, колебаний тока возбуждения генератора Iв, изменения сопротивления цепи якоря вследствие изменения температуры и т.д.
При замыкании контактов «3-4» (рис. 1.4) устанавливается обратная связь между входной и выходной величинами, в результате чего величина напряжения генератора Uг поддерживается управляющим устройством постоянной и равной с точностью до DU напряжению Uвх независимо от действия внешних и внутренних возмущений. Процессы в отдельных элементах рассматриваемой системы без учета инерционностей можно описать приближенными уравнениями.
Уравнение замыкания системы
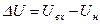 , (1.4)
, (1.4)
где
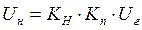 , (1.5)
, (1.5)
UH - напряжение на выходе измерителя напряжения;
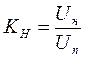 (1.6)
(1.6)
KH - коэффициент передачи датчика напряжения;
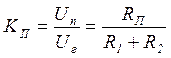 , (1.7)
, (1.7)
КП - коэффициент усиления потенциометра.
Величины Uвх и Uн на входе операционного усилителя включены так, что
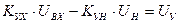 , (1.8)
, (1.8)
где
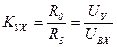 , (1.9)
, (1.9)
КУХ - коэффициент усиления по отношению к входной величине Uвх;

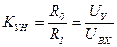 (1.10)
(1.10)
КУН - коэффициент усиления по отношению к величине Uн.
Уравнение (1.8) можно переписать в виде:
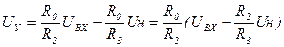 , (1.11)
, (1.11)
При R2=R3, Kyx=Kун=Kу уравнение для усилителя можно представить в виде
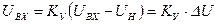 , (1.12)
, (1.12)
Уравнение для тиристорного преобразователя в упрощенном виде также можно представить пропорциональным звеном
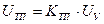 , (1.13)
, (1.13)
где Kтп - коэффициент передачи тиристорного преобразователя.
Коэффициент усиления генератора будет
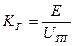 , (1.14)
, (1.14)
а уравнение электрического равновесия для генератора
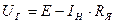 , (1.15)
, (1.15)
Пренебрегая реакцией якоря и влиянием насыщения магнитной цепи в первом приближении можно принять
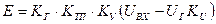 , (1.16)
, (1.16)
Тогда уравнение (1.15) можно переписать в виде
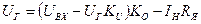 , (1.17)
, (1.17)
или
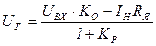 , (1.18)
, (1.18)
где 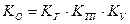 ;
; 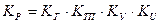
Структурная схема, соответствующая уравнениям (1.12), (1.13), (1.18) представлена на рисунке 1.7.
Исключив из уравнений (1.12, 1.13, 1.18) промежуточные переменные, установим связь между рассогласованием (ошибкой регулирования) DU, входной величиной и падением напряжения IнRя
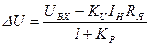 , (1.19)
, (1.19)
Пренебрегая ошибкой по управлению, получим:
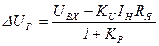 , (1.19а)
, (1.19а)
где 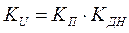 - коэффициент измерителя напряжения.
- коэффициент измерителя напряжения.
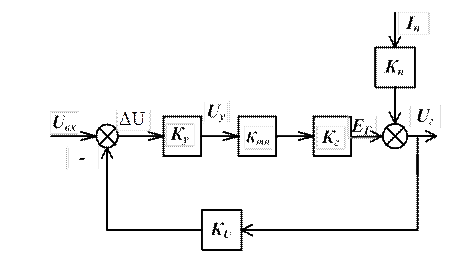
Рисунок 1.7 Структурная схема замкнутой САУ
Из выражения (1.19) видно, что при достаточно большом Kр ошибку регулирования DU можно сделать сколь угодно малой, то есть включение обратной связи уменьшает влияние возмущающего воздействия на выходную величину в Kp раз.
В рассматриваемом примере
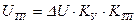 , (1.20)
, (1.20)
т.е. управляющее воздействие пропорционально отклонению регулируемой величины от требуемого значения. При таком алгоритме управления, как показал анализ, отклонение DU в установившемся статическом режиме при включении автоматического управляющего устройства только уменьшается. Для полного устранения отклонения в установившемся режиме управляющее воздействие должно быть более сложной функцией отклонения, зависящей не только от его величины и знака, но и от его интегралов и производных.
Из приведенного анализа видно, что системы с принципом управления по отклонению обладают рядом важных достоинств.
Уменьшают отклонение выходной величины от требуемого значения независимо от того, какими факторами оно вызвано.
Менее чувствительны к изменениям параметров элементов системы по сравнению с разомкнутыми системами.
Принцип управления по отклонению применим для объектов, точные характеристики которых определить невозможно.
К недостаткам этого принципа можно отнести следующее.
В системах с принципом управления по отклонению как в замкнутых системах возникает проблема устойчивости.
В простых одноконтурных системах с принципом управления по отклонению нельзя полностью исключить влияние возмущающего воздействия на выходную величину (т.е. достичь абсолютной инвариантности).
Однако благодаря существенным преимуществам системы с принципом управления по отклонению нашли широкое распространение в технике.
