Исследовать сходимость ряда № 1 - 13
№1. 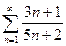 . №2.
. №2. 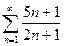 . №3.
. №3. 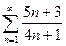 . №4.
. №4. 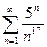 .
.
№5. 
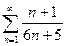 . №6..
. №6.. 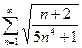 №7.
№7. 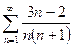 . №8.
. №8. 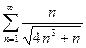 .
.
№9. 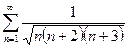 . №10.
. №10. 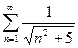 . №11.
. №11. 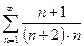 .
.
№12. 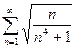 . №13.
. №13. 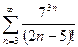 .
.
Определение: Знакопостоянный числовой ряд-это такой ряд, все члены которого либо только положительные, либо отрицательные числа.
| № | Название | Формулировка | Примечание |
| Признак Д’Аламбера | Если у знакоположительного ряда 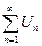 существует и конечен существует и конечен 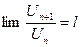 , то, если , то, если 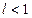 , ряд сходится; если , ряд сходится; если 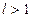 ,то ряд расходится. Замечание: Если ,то ряд расходится. Замечание: Если 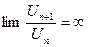 , то ряд расходится , то ряд расходится | 1.Применяется, если общий член ряда содержит слагаемым или множителем 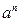 или или 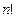 , или их вариации 2. Если , или их вариации 2. Если 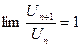 , вопрос о сходимости ряда остается открытым , вопрос о сходимости ряда остается открытым | |
| Радикальный признак Коши | Если у знакоположительного ряда 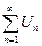 существует и конечен существует и конечен 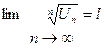 , если , если 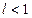 , ряд сходится; если , ряд сходится; если 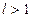 ,то ряд расходится ,то ряд расходится | 1. Применяется, если общий член ряда целиком является n – ой ( или n+1 – ой, 2n –ой…) степенью некоторого выражения 2. Если l = 1, вопрос о сходимости ряда остается открытым | |
| Интегральный признак Коши | Если функция 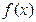 - непрерывная, положительная, убывающая при - непрерывная, положительная, убывающая при 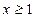 и и 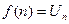 , то ряд , то ряд 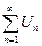 и несобственный интеграл и несобственный интеграл 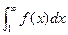 одновременно сходятся или расходятся. одновременно сходятся или расходятся. | 1. Применяется, когда общий член 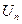 порождает функцию порождает функцию 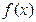 , первообразная которой находится без особого труда , первообразная которой находится без особого труда |
Примерный план исследования знакоположительного ряда:
1. Определить вид ряда.
2. Находят (если это не трудно) 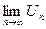 :
: 
а) если 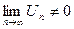 , то ряд расходится
, то ряд расходится
б) если 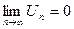 , то продолжаем исследование.
, то продолжаем исследование.
3. Устанавливаем путем анализа формулы общего члена какой из признаков целесообразнее применить, перебирая признаки в следующем порядке:
а) признак Д’Аламбера
б) радикальный признак Коши
в) интегральный признак Коши
г) признаки сравнения
4. Исследуем сходимость ряда по данному признаку
Степень роста выражений при 
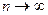
1. 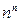
2. 
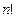
3. 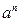 ,
, 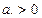
4. 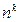 ,
, 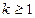
5. 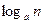 ,
, 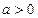
Исследовать на сходимость №№ 14 – 18.
№14. 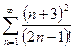 . №15.
. №15. 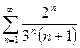 . №16.
. №16. 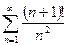 . №17.
. №17. 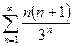 .
.
№18. 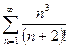 . №19.
. №19. 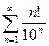 №20.
№20. 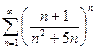 №21.
№21. 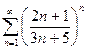
Знакопеременные ряды
Знакопеременные ряды – это числовые ряды, содержащие бесчисленное множество положительных и бесчисленное множество отрицательных членов
Определение: Знакопеременный ряд, у которого положительные и отрицательные члены ряда следуют строго друг за другом называется знакочередующимся
Теорема (Признак Лейбница)
Если абсолютные величины членов знакочередующегосяряда убывая стремятся к нулю, то такой ряд сходится и абсолютная величина его суммы не превосходит первого члена ряда.
Ряд, удовлетворяющий признаку Лейбница, называется рядом Лейбница или лейбницевским рядом. Он всегда сходится
Определение. Ряд 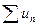 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 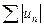 .
.
Определение. Ряд 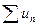 называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 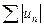 расходится.
расходится.
№22. 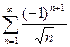 . №23.
. №23. 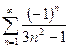 . №24.
. №24. 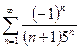 . №25.
. №25. 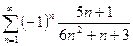 . №26.
. №26. 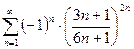 . №27.
. №27. 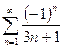 . №28.
. №28. 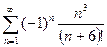
Степенные ряды
Определение: Ряд, все члены которого являются функциями одного и того же аргумента, называется функциональным.
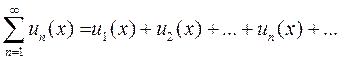
Ряд, записанный в виде
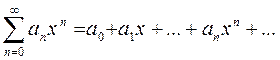
называется степенным
План нахождение области сходимости:
1) Найдем радиус сходимости по одной из формул 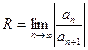 или
или 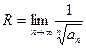
2) Запишем интервал сходимости (-R: R),
3) Дополнительно исследуем сходимость заданного ряда в точках x = 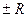
4) Записываем область сходимости исходного ряда.
Замечание:
Если исследуем ряд, расположенных по степеням (x – x0), где x0 ≠ 0, общий вид которого
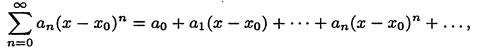 то
то
выполним замену x – x0 = X, получим 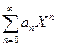 (1)и найдем область сходимости полученного ряда по плану, затем заменив X, найдем область сходимости исходного ряда
(1)и найдем область сходимости полученного ряда по плану, затем заменив X, найдем область сходимости исходного ряда
Найти область сходимости степенных рядов:
№29. 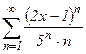 . №30.
. №30. 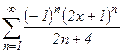 . №31.
. №31. 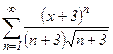 .
.
№32. 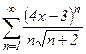 . №33.
. №33. 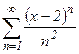 . №34.
. №34. 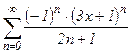 .
.
№35. 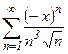 . №36.
. №36. 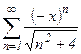 . №37.
. №37. 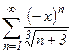 .
.
№38. 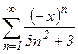 . №39.
. №39. 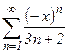 .
.
Разложить в ряд по степеням 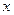 :
:
№40. 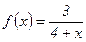 №41.
№41. 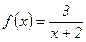 . №42.
. №42. 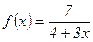 .
.
№43. 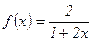 .№44.
.№44. 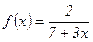 . №45.
. №45. 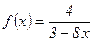 .
.
№46. 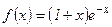 . №47.
. №47. 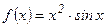 .№44.
.№44. 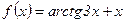 .
.
№45. 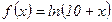 . №46.
. №46. 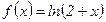 . №47.
. №47. 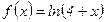 .
.
Вопросы по теме «Ряды»
1.Основные понятия о числовых рядах. Свойства числовых рядов.
