Задания для самостоятельной работы. 1. Найти математическое ожидание случайной величины Z, если известны математические ожидания и :
1. Найти математическое ожидание случайной величины Z, если известны математические ожидания 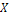 и
и 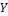 :
: 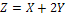 ,
, 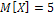 ,
, 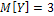 .
.
2. Найти: а) математическое ожидание, б) дисперсию, в) среднее квадратическое отклонение дискретной случайной величины X по известному закону ее распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке - соответствующие им вероятности).

3. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения и вычислить числовые характеристики ДСВ X - числа стандартных деталей среди отобранных.
Вопросы для самоконтроля:
1. Дайте понятие дискретной случайной величины. Приведите примеры.
2. Как задать закон распределения дискретной случайной величины?
3. Назовите основные характеристики случайной величины.
4. Как находится математическое ожидание дискретной случайной величины?
5. Дайте определение дисперсии дискретной случайной величины.
6. Как находится среднее квадратическое отклонение случайной величины?
7. По каким формулам вычисляется дисперсия дискретной случайной величины?
