ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА, МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. Проекция точки на множество
Выпуклое множество.
Проекция точки на множество.
Формулировки двух лемм о свойствах проекции.
Определение отделимости точки и множества, строгая и сильная отделимость.
Две теоремы об отделимости (с доказательствами).
Выпуклая, строго выпуклая функция (вогнутая и строго вогнутая).
Свойства выпуклых функций (критерии выпуклости – с доказательством).
Задача выпуклого математического программирования и ее свойства.
Правило отсечений по измерению градиента выпуклой функции областей, не содержащих глобального минимума.
Производная по направлению, ее вычисление для дифференцируемой функции.
Функция Лагранжа для общей задачи мат. программирования.
Активные ограничения. Условие дополняющей нежесткости.
Теорема Ферма (с доказательством).
Теорема Лагранжа.
Усиленная теорема Лагранжа для выпуклого случая.
Теорема Куна-Таккера для выпуклого недифференцируемого случая.
Теорема Куна-Таккера в терминах седловой точки.
Теорема Каруша-Куна-Таккера в дифференциальной форме (выпуклый и невыпуклый случаи).
Определение регулярности допустимой области в точке и регулярности области в целом.
Достаточное условие регулярности Слейтера .
Достаточное условие регулярности в форме линейной независимости (с доказательством).
Понятие метода поисковой оптимизации.
Определение пассивного алгоритма, последовательного алгоритма.
Оптимальные и e–оптимальные алгоритмы.
Определение унимодальной функции.
Правило сокращения интервала. Гарантированная неопределенность после N измерений.
Оптимальные и e–оптимальные пассивные N–шаговые алгоритмы для унимод. функц.(с объяснением).
Алгоритм метода Фибоначчи. Формула для его гарантированной эффективности.
Метод золотого сечения. Формула для его гарантированной эффективности.
Методы дихотомии. Формула для его гарантированной эффективности.
Общая структура итерационных методов локального поиска в 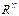 .
.
Порядок метода поисковой оптимизации.
Линейная, сверхлинейная и квадратичная скорость сходимости.
Два критерия выбора шагового множителя.
Алгоритмы Армихо и одномерной минимизации.
Алгоритм метода наискорейшего градиентного поиска. Демонстрация применения.
Его свойства, соотношение Канторовича – оценка скорости сходимости.
Метод Ньютона (с выводом основного соотношения).
Теорема о сходимости и порядке сходимости для метода Ньютона.
Метод прямого поиска: метод Хука-Дживса.
Методы Ньютона–Рафсона и Флетчера–Ривса (по материалам лабораторной работы).
Метод внешних штрафных функций – описание применения.
Вид степенной функции штрафа.
Влияние показателя степени в степенном штрафе на гладкость функции штрафа.
Теорема сходимости метода внешнего штрафа.
Определение Липшицевой функции.
Свойства липшицевых функций.
Вид верхней и нижней оценок функции по результатам k измерений.
Оценки глобального минимума по значению функции и координатам (по результатам k измерений).
Метод Пиявского – описание алгоритма. Демонстрация применения.
Теорема сходимости метода Пиявского.
Одномерный вариант метода Пиявского — метод ломанных.
Метод деления на три – описание алгоритма. Демонстрация применения.
