Проверка адекватности модели

Эта проверка проводится с целью определения соответствия модели экспериментальным данным. Используется F-критерий (Фишера), который представляет собой отношение дисперсии адекватности или остаточной дисперсии к дисперсии воспроизводимости

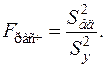
Полученное значение сравнивается с табличным значением F_крит (f_ад, f_y), найденным при числе степеней свободы f_ад =N – d и f_y =N (m–1). Если F_расч< F_крит, то принимается гипотеза об адекватности построенной модели результатам эксперимента.

Если F_расч > F_крит, то линейная модель не является адекватной. В этом случае она дополняется нелинейными членами или переходят к построению планов второго порядка и т.д.

Дисперсия адекватности (остаточная) определяется по формуле

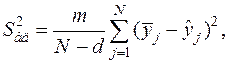
где d — число членов аппроксимирующего полинома (уравнения регрессии);

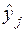— оценка целевой функции (параметра оптимизации) по принятой модели в каждом j-м опыте.

Построение математической модели для действительных значений факторов

В результате проведения эксперимента получается математическая модель в кодированных значениях факторов. Для получения математической модели в натуральных (действительных) значениях факторов необходимо заменить кодированные значения натуральными, т.е. подставить в модель

.

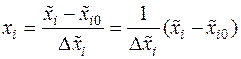Значения 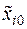и 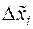известны, так как они выбираются перед составлением плана эксперимента. После подстановки кодированных значений всех факторов и выполнения необходимых преобразований получим модель в натуральных значениях факторов с новыми коэффициентами регрессии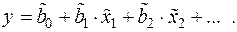

Планы второго порядка

Методы планирования эксперимента используются при решении задач оптимизации. При этом используются два подхода. Первый подход состоит в том, что когда нужно исследовать поверхность отклика, далекую от области экстремума, то достаточно знать направление движения в область оптимизации и не обязательно знать точное описание поверхности отклика. В градиентных методах для выбора направления движения определяются составляющие градиента, которые представляют собой коэффициенты линейного уравнения регрессии 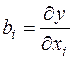. Поэтому при первом подходе используются планы первого порядка, по которым проводится полный или дробный факторный эксперимент.

Второй подход используется при приближении к области экстремума, когда требуется более точное описание поверхности отклика. Используются, как правило, планы второго порядка, которые позволяют получить квадратичную модель. Для этого к плану, по которому строится линейная модель, добавляются новые опыты, чтобы более подробно описать поверхность отклика. При этом бóльшую часть эксперимента следует проводить в области оптимума, т.е. в «почти стационарной» области. Её обычно удается описать полиномом второго порядка

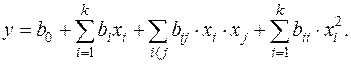
Для оценки коэффициентов регрессии такого полинома при ПФЭ типа 2^k не хватает количества точек, в которых проводятся опыты. Это значит, что факторы надо менять не в двух уровнях, а не менее чем в трех. Используются композиционные планы, которые позволяют сократить число опытов. Эти планы состоят в том, что к плану ПФЭ или ДФЭ, в случае неадекватности линейной модели, добавляются точки, расположенные симметрично относительно центра плана. Они носят название «звездные точки» и прибавляются по две на каждую координату (переменную) x_i на расстоянии α от центра. α — «звездное плечо». Еще одна точка (или несколько) добавляется в центре эксперимента (рис. 3.3 для k = 3).

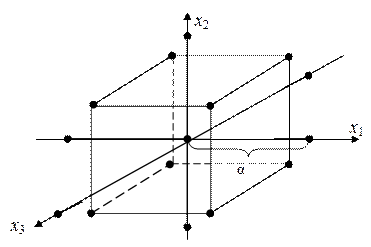
Рисунок 3.3 — «Звездные точки» при k=3

В результате получаем варьирование каждого фактора в пяти уровнях:

– α, –1, 0, +1, + α,

т.е. на оси каждого фактора имеется пять точек.

Натуральное расстояние до «звездной точки» определяется следующим образом: 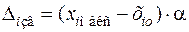, тогда значения фактора в «звездных точках» будут

.

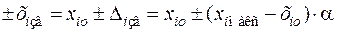Полученные значения округляются до удобных величин. Например, время изменяется от 57 мин до 83 мин. Среднее время 70 мин. Тогда 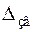= (83–70)∙1,55=20,2 мин. Значения этого фактора в звездных точках будут 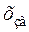= 70 ± 20,2 = (–50… + 90) мин.

При k = 3 точки в вершинах куба представляют собой точки исходного ПФЭ типа 2³, или ядро планирования.

При расположении всех добавленных точек симметрично относительно центра плана получаем центральный композиционный план (ЦКП).

Планы второго порядка не обладают одновременно свойствами ортогональности и ротатабельности. Существуют ортогональные ЦКП и ротатабельные ЦКП.

Общее число опытов композиционного плана при k факторах равно

N = 2^k + 2k + n₀,

где 2^k — число опытов в ПФЭ (в ДФЭ будет 2^k–р);

2k — число «звездных точек»;

n₀ — число опытов в центре плана.

Ортогональные ЦКП

Для того чтобы ЦКП получил свойства ортогональности, необходимо обеспечить эти свойства для столбцов, соответствующих фиктивной переменной и квадратам факторов, так как они все имеют значения +1. Следовательно, попарные произведения этих столбцов не будут равны нулю. Введение «звездных точек», для которых расстояние α выбирается в зависимости от размерности (числа факторов k), обеспечивает условие ортогональности квадратичных столбцов (табл. 3.8). В центре плана достаточно провести испытание в одной точке. Начиная с k = 5 можно в качестве планов первого порядка использовать ДФЭ.

Таблица 3.8

Параметры плана	Число независимых переменных k
Ядро планирования   Расстояние α	22   1,000	23   1,215	24   1,414	25–1   1,547

В ортогональных центральных композиционных планах (ОЦКП) коэффициенты регрессии определяются независимо друг от друга, но их дисперсии будут различными, поскольку этот план не является ротатабельным. Кроме того, изменится уравнение регрессии, так как для обеспечения условий ортогональности необходимо вводить преобразование квадратов переменных [12, 15, 16].

Матрица ОЦКП имеет вид (табл. 3.9).

Таблица 3.9

Виды точек	Номер опыта (точки)	х0	х1	х2	х1· х2		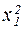	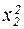y
Точки ядра плана 22		+ + + +	– + – +	– – + +	+ – – +	+ + + +	+ + + +	y1 y2 y3 y4
«Звездные точки»		+ + + +	+α –α	+α –α		α2 α2	α2 α2	y5 y6 y7 y8
Центральная точка		+						y9

Ротатабельные ЦКП

Свойство ротатабельности предполагает, что дисперсия параметра оптимизации

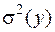= const при R = const.

Для выполнения этого условия в ЦКП добавляют «звездные точки» на расстоянии α = 2 ^k/4 для ПФЭ типа 2 ^k и α = 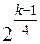для ДФЭ типа 2 ^k–1 по две на каждый фактор и несколько точек в центре плана в соответствии с табл. 3.10 [16]. Число центральных точек выбирается в таком количестве, чтобы обеспечить униформость плана, т.е. неизменность дисперсии параметра оптимизации внутри области планирования (на некотором расстоянии R от центра плана).

Таблица 3.10

Параметры плана	Число независимых переменных k
Ядро планирования Расстояние α Число центральных точек n0	22 1,414	23 1,682	24 2,000	25–1 2,000

Определение коэффициентов регрессии и их дисперсий после проведения РЦКП значительно сложнее, чем при ОЦКП.

Матрица РЦКП имеет вид (табл. 3.11).

Таблица 3.11

Виды точек	Номер опыта (точки)	х0	х1	х2	х1· х2		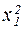	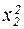y
Точки ядра плана 22		+ + + +	– + – +	– – + +	+ – – +	+ + + +	+ + + +	y1 y2 y3 y4
«Звездные точки»		+ + + +	+α –α	+α –α		α2 α2	α2 α2	y5 y6 y7 y8
Центральные точки (в центре плана)		+ + + + +						y9 y10 y11 y12 y13

Если на независимые переменные (факторы) накладываются ограничения, т.е. указывается диапазон изменения каждого фактора, то точки выбираются следующим образом. На каждой оси факторного пространства выделяются также пять точек: центральная, соответствующая середине диапазона, две точки на его краях, называемые «звездными», и две промежуточные точки, расстояния до которых в α раз меньше, чем до звездных. Тогда матрица плана строится так, что точки ядра плана соответствуют промежуточным точкам, а «звездные точки» соответствуют точкам на краях диапазона. Рассмотрим это на примере, приведенном в [20].

Рассматривались целевые функции усилителя R_вx и K_ие, которые зависят от сопротивлений R_г, R_ос, R_н, которые изменяются в диапазонах: R_Г = 0,1 … 1,1 кОм; R_ос=2,0…4,0 кОм; R_н= 0,8…4,2 кОм. Эти значения берутся в качестве звездных точек. Промежуточные точки определяются следующим образом. Так как имеем 3 фактора, то для ротатабельного плана α = 2^k/4 = 1,68. Средние значения сопротивлений будут: R_г.ср= 0,6 кОм; R_ос.ср= 3,0 кОм; R_н.ср = = 2,5 кОм. Они определяют центр плана.

Тогда значения промежуточных точек составляют для R_г:

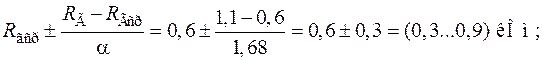
для R_ос:

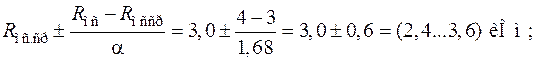
для R_н:

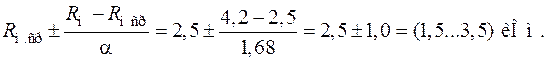
Матрица плана (фрагмент) для натуральных значений факторов приведена в табл. 3.12.

Таблица 3.12

Виды точек	Номер точки	Факторы	Факторы
Rг	Rос	Rн	х1	х2	х3
Точки ядра плана 23		0,3 0,9 0,3 0,9 0,3 0,9 0,3 0,9	2,4 2,4 3,6 3,6 2,4 2,4 3,6 3,6	1,5 1,5 1,5 1,5 3,5 3,5 3,5 3,5	– + – + – + – +	– – + + – – + +	– – – – + + + +
«Звездные точки»		0,1 1,1 0,6 0,6 0,6 0,6	3,0 3,0 2,0 4,0 3,0 3,0	2,5 2,5 2,5 2,5 0,8 4,2	–(α) +(α)	–(α) +(α)	–(α) +(α)
Центральные точки (в центре плана)		0,6 0,6 0,6 0,6 0,6 0,6	3,0 3,0 3,0 3,0 3,0 3,0	2,5 2,5 2,5 2,5 2,5 2,5

В матрице «звездное плечо» α взято в скобки, как условно соответствующее «звездным точкам».

Другие разновидности планов эксперимента

Кроме рассмотренных ранее ПФЭ, ДФЭ и планов 2-го порядка, используются и другие планы. Так, для уменьшения количества факторов осуществляют планирование отсеивающих экспериментов (метод случайного баланса, планы последовательного отсеивания и др.) [15, 16, 21]. Они используются до проведения тех экспериментов, по результатам которых определяются коэффициенты регрессии.

При определении оценок коэффициентов регрессии полагают, что они принадлежат некоторому эллипсоиду рассеивания.

Различают Д-, А- и Е-оптимальные планы.

Для минимизации объема эллипсоида рассеивания используют Д-оптимальный план.

А-оптимальный план минимизирует сумму квадратов главных полуосей эллипсоида рассеивания.

Е-оптимальный план минимизирует максимальную ось эллипсоида рассеивания.

G-оптимальный план, в отличие от предыдущих, относится к оценкам параметра оптимизации (функции отклика). Это план, при котором обеспечивается наименьшее значение их дисперсии.

Все эти планы применяются в зависимости от решаемых задач.

Вопросы для самопроверки

1. Какое уравнение используется в качестве математической модели в активном эксперименте?

2. Какие концепции лежат в основе активного эксперимента? В чем они состоят?

3. Что такое план первого порядка, план второго порядка?

4. Какие бывают виды активного эксперимента?

5. Что такое матрица планирования?

6. Как выбираются область эксперимента, основной уровень и интервалы изменения факторов?

7. Что такое полный факторный эксперимент?

8. В скольких уровнях меняются факторы для получения линейной модели?

9. Что такое эффект фактора и эффект взаимодействия?

10. Назовите свойства отдельных столбцов матрицы ПФЭ.

11. Назовите свойства совокупности столбцов матрицы ПФЭ. Что они означают?

12. Что такое дробный факторный эксперимент? Для чего он используется?

13. Как строится план ДФЭ?

14. Что такое дробная реплика?

15. Что такое генерирующее соотношение?

16. Что такое определяющий контраст?

17. Что такое смешанные и несмешанные оценки коэффициентов регрессии?

18. Что такое система смешивания?

19. Как определяются коэффициенты регрессии в ПФЭ.

20. Какие проводятся проверки в активном эксперименте? Какие критерии для этого используются?

21. Когда приходится переходить к планам второго порядка?

22. Как получаются центральные композиционные планы (ЦКП)?

23. Что представляет собой ядро планирования?

24. Какие бывают ЦКП?

25. Каково число опытов в ЦКП?

26. Как определяется «звездное плечо» α?

27. Сколько опытов проводится в центре плана ОЦКП и РЦКП?

Литература

1. Перегудов Ф.И., Тарасенко Ф.П. Основы системного анализа: Учебник. — 2-е изд., доп. — Томск: Изд-во НТЛ, 1997.

2. Веников В.А. Теория подобия и моделирования (применительно к задачам электроэнергетики): Учеб. пособие для вузов. — 2-е изд., доп. и перераб. — М.: Высшая школа, 1976.

3. Длин А.М. Математическая статистика в технике. — М.: Советская наука, 1958.

4. Мудров В.И., Кушко В.Л. Методы обработки измерений. — М.: Сов.радио, 1976.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. — М.: Высшая школа, 1977.

6. Душинский В.В., Пуховский Е.С., Радченко С.Г. Оптимизация технологических процессов в машиностроении. — К.: Изд-во «Технiка», 1977.

7. Коваленко Е.С., Киселев О.Н., Шарыгин Г.С. Основы научных исследований: Учебное пособие. — Томск: Изд-во Томского ун-та, 1988.

8. Смирнов Н.В., Дунин-Барковский И.В. Краткий курс математической статистики для технических приложений. — М.: Физматгиз, 1959.

9. Серафинович Л.П. Статистическая обработка опытных данных. — Томск: ТУСУР, 1999.

10. Колкер Я.Д. Математический анализ точности механической обработки деталей. — Киев: Изд-во «Технiка», 1976.

11. Герасимович А.И., Матвеева Я.И. Математическая статистика. — Минск: Высшая школа, 1978.

12. Сыпчук П.П., Талалай А.М. Методы статистического анализа при управлении качеством изготовления элементов РЭА. — М.: Сов. радио, 1979.

13. Головач А.В. и др. Критерии математической статистики в экономических исследованиях. — М.: Статистика, 1973.

14. Нейман Ю. Вводный курс теории вероятностей и математической статистики: Пер. с англ. — М.: Наука, 1968.

15. Кориков А.М. Математические методы планирования эксперимента: Учебное пособие. — Томск: Изд-во Томского университета, 1973.

16. Решетников М.Т. Планирование эксперимента и статистическая обработка данных: Учебное пособие. — Томск: ТУСУР, 2000.

17. Черемошенский В.В. Применение метода статистического планирования эксперимента для анализа надежности радиоизмерений по неполным отказам // Вопросы надежности и точности радиоэлектронной аппаратуры / Под ред. А.В. Фомина. — М.: Труды МАИ. — 1970. — Вып. 2.

18. Глудкин О.П. и др. Статистические методы в технологии производства радиоэлектронной аппаратуры / Под ред. В.Н. Черняева. — М.: Энергия, 1977.

19. Налимов В.В., Голикова И.М. Логические основания планирования эксперимента. — М.: Металлургия, 1976.

20. Налимов В.В., Чернова И.А. Статистические методы планирования экстремальных экспериментов. — М.: Наука, 1965.

21. Яншин А.А. Теоретические основы конструирования, технологии и надежности ЭВА: Учебное пособие для вузов. — М.: Радио и связь, 1983.

22. Сборник задач и упражнений по технологии РЭА: Учеб. пособие / Под ред. Е.М. Парфенова. — М.: Высш. школа, 1982.