Обработка результатов экспериментов. Их достоверность
При обработке эксперимента очень важно наилучшим образом выбрать форму представления его результатов. Поэтому экспериментальные исследования, проводимые как в натуре, так и на моделях, должны быть предварительно тщательно продуманы не только в отношении порядка их проведения, но и в отношении выбора методов обработки результатов (методов получения оценок).
В соответствии с целями методы получения оценок можно разделить на две большие группы.
В методах первой группы оперируют с функциями распределения наблюдаемых величин. При этом характер функции распределения предполагается известным, а неизвестным являются лишь их некоторые числовые параметры. Среди этих методов наиболее широкое использование получили метод моментов, метод максимального правдоподобия (наибольшего правдоподобия), байесовский метод, метод условных математических ожиданий. Как частные случаи этих методов при определённых предположениях относительно вида функции распределения наблюдаемых величин выступают метод наименьших квадратов, метод наименьших положительно определённых форм, являющийся обобщением метода наименьших квадратов, метод наименьших модулей и др.
В методах второй группы не требуется знание функций распределения. Здесь в основе классификации лежит формальная вычислительная схема, используемая для получения оценок. К этим методам относятся: метод наименьших квадратов, метод наименьших положительно определённых квадратичных форм, метод наименьших модулей, метод минимакса, метод Коши и др.
Если сделать какие-то предположения о характере функций распределения измерений, то почти каждый метод второй группы можно рассматривать как следствие или частный случай методов первой группы и тогда они получают теоретическое обоснование. Если же не делать таких предположений, то эти методы остаются чисто формальными и тогда возникает законный вопрос: как ведёт себя каждый из этих формальных методов в условиях, когда ошибки измерения подчинены тому или иному закону распределения вероятностей?
Существует теснейшая связь между методом максимального правдоподобия, нормальным распределением ошибок и методом наименьших квадратов, а именно, если ошибки измерений подчиняются нормальному закону распределения, то метод максимального правдоподобия сводится к методу наименьших квадратов [4].
Выбор методов обработки результатов эксперимента зависит от целей эксперимента:
– определение статистических характеристик исследуемого процесса или какой-то статистической совокупности объектов;
– проверка научной гипотезы и нахождение математической модели исследуемого объекта или процесса.
В первом случае проводится так называемая первичная или предварительная обработка (анализ) экспериментальных данных: определяются средние, дисперсии, их интервальные оценки, функция распределения и т.п. Например, используется статистический контроль качества продукции. В этом случае решающее значение в планировании эксперимента и его обработке приобретает принцип максимума правдоподобия.
Во втором случае полученные значения переменных наносят на график и по его общему виду подбирают тип математической модели.
В более общем случае эта модель представляется в виде полинома или уравнения регрессии, коэффициенты которого определяются по методу наименьших квадратов.
Обычно в практических приложениях оценка достоверности результатов моделирования с учётом погрешности задания и воспроизведения критериев подобия при статистических их вариациях сводится к двум задачам:
– оценка погрешности реализации приближённого моделирования вместо точного;
– оценка влияния стохастических вариаций критериев подобия.
Вопрос о достоверности статистических выводов в основном решается в зависимости от трёх моментов:
– от абсолютной величины самой полученной разности двух сопоставляемых средних;
– от числа производимых наблюдений;
– от размаха случайных колебаний исходных значений.
Для оценки достоверности вычисляют меру случайного варьирования отдельных значений [3].
Ошибки и гипотезы
После проведения эксперимента имеется набор выборочных данных. На основе этого набора данных необходимо принимать решения. Естественно, требуется оценить, какие при этом могут быть совершены ошибки. Различают ошибки двух типов или двух родов.
Ошибка I-го рода — a — заключается в том, что отвергается решение, которое на самом деле является правильным. При статистическом контроле качества продукции эту ошибку называют риском поставщика. Она означает вероятность забракования кондиционной продукции при её приёмке как негодной. Величина a служит уровнем значимости. Уровень значимости a — это минимальная вероятность, начиная с которой событие признаётся практически невозможным. Обычно a выбирается из ряда 0,001; 0,005; 0,01; 0,02; 0,05; 0,1; 0,2; 0,3. Величина P = 1 – a называется надёжностью вывода, или доверительной вероятностью.
Ошибка II-го рода— b — заключается в том, что принимается решение, которое на самом деле является неверным. При статистическом контроле качества продукции эту ошибку называют риском заказчика (потребителя).
Очевидно, что выбор значений a и b должен зависеть от последствий совершения ошибок первого и второго рода соответственно. Чем серьёзнее эти последствия, тем меньше должен быть уровень значимости. Выбирая уровень значимости, следует также учитывать мощность критерия. Критерий должен быть построен таким образом, чтобы вероятность отклонить испытуемую гипотезу, когда она верна (a), была минимальной, а когда верна альтернативная гипотеза (1 – b) — максимальной, т.е. вероятности ошибок I и II рода должны быть минимальными. Вероятности этих ошибок взаимосвязаны: с уменьшением вероятности ошибки I рода мощность критерия уменьшается; он хуже улавливает различия между гипотезами. Вероятность ошибки II рода при этом увеличивается [13]. Единственный способ уменьшить эти ошибки состоит в увеличении объёма выборки.
Естественно, что ошибка второго рода более опасна, так как поставщик может провести повторную проверку качества продукции, а заказчик лишен этой возможности из-за отправки этой продукции с завода-изготовителя.
Ошибка первого рода a или доверительная вероятность P используются при проверке статистических гипотез.
Статистическая гипотеза — H — это некоторое утверждение относительно распределений совокупности случайных величин или всякое предположение об истинных значениях параметров подбираемой модели для экспериментальных данных или о её типе. Различают нулевую и альтернативную гипотезы.
Нулевая гипотеза — H0 — это гипотеза, утверждающая, что различие между сравниваемыми величинами отсутствует, т.е. разница между оценками случайная и параметры генеральных совокупностей одинаковы, не имеют различия (разница равна нулю). Наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках. Все остальные гипотезы, отличающиеся от нулевой, называются альтернативными H1, H2 и т.п.
Альтернативная гипотеза — предположение, противоположное нулевой гипотезе. Следовательно, можно сказать, что ошибка первого рода — это ошибка отклонения верной гипотезы, а ошибка второго рода — это ошибка принятия ложной гипотезы. Величину 1 – b называют мощностью критерия. Это вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.
Гипотезы всегда формулируются относительно генеральных (истинных) параметров распределений, которые справедливы для рассматриваемых случайных величин. Но правила проверки гипотез строятся на основании выборочных значений параметров. Перед анализом выборки фиксируется уровень значимости a. В соответствии с выбранным значением a определяется критическая граница, за которую не могут выходить оцениваемые критерии. Отвечающую уровню значимости область называют критической областью. Иными словами, критической областью называют совокупность значений критериев, при которых нулевую гипотезу отвергают. Критерием проверки статистических гипотез или просто критерием — K — называют случайную величину, которая служит для проверки гипотезы (критерии Стьюдента, Фишера, Пирсона и др.).
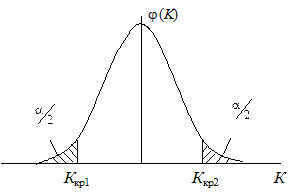
Выборочное пространство для всех возможных значений статистики, лежащей в основе критерия для проверки гипотезы, разбивают на две части: область допустимых значений и критическую область, в которой гипотеза отвергается. Критическая область может быть двусторонняя и односторонняя (рис. 1.2).
 | 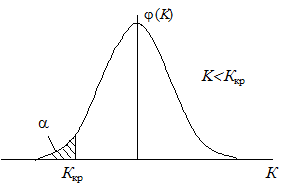 |
| а | б |
Рисунок 1.2 — Критические области (заштрихованы)
а — двусторонняя; б — односторонняя
Вероятность попадания в заштрихованную область равна 1 – P. Вероятность попадания в границы Kкр1, Kкр2 равна 1 – a.
Критическими точками (границами) Kкр называют точки, отделяющие критическую область от области принятия гипотезы.
Правосторонней называют критическую область, определяемую неравенством K > Kкр, где Kкр — положительное число.
Левосторонней называют критическую область, определяемую неравенством K < Kкр, где Kкр — отрицательное число.
Двусторонней называют критическую область, определяемую неравенством K < Kкр1, K > Kкр2, где Kкр2 > Kкр1.
Для отыскания критической области задаются уровнем значимости a и по соответствующим таблицам ищут критические точки, исходя из следующих соотношений:
а) для правосторонней критической области
P (K > Kкр) = a, Kкр > 0;
б) для левосторонней критической области
P (K < Kкр) = a, Kкр < 0;
в) для двусторонней симметричной области
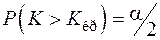 ,
, 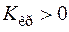 ,
, 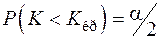 ,
, 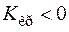 .
.
На рис. 1.3. приведены плотности распределения критериев при условии верности гипотез H0 и H1.
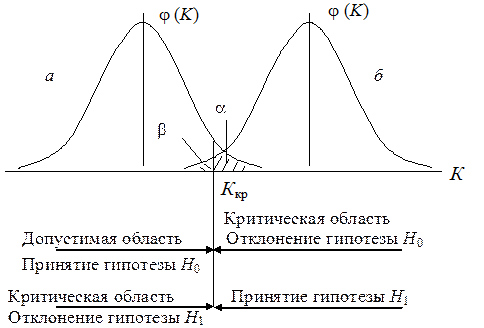 |
Рисунок 1.3 — Распределение критериев:
а — при условии, что верна гипотеза H0; б — при условии,
что верна гипотеза H1
