Методи оптимізації амплітудної характеристики
При проектуванні систем управління об'єктами, що не містять чистого запізнювання, найбільше застосування одержали два критерії - модульний оптимум (МО) і симетричний оптимум (СО).
Критерій модульного оптимуму, називаний також критерієм амплітудного або технічного оптимуму, полягає у виконанні наступних вимог до форми амплітудної характеристики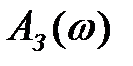 
замкнутої системи (Рисунок 1): характеристика в як можна більше широкому діапазоні частот повинна бути горизонтальною і рівною одиниці; похила ділянка характеристики повинен бути як можна більше крутопадаючою. Інакше кажучи, критерій модульного оптимуму вимагає, щоб настроювана система наближалася по своїх частотних передатних властивостях до ідеального фільтра низької частоти, що має, як відомо, прямокутну частотну характеристику с. 
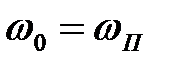Тоді при відсутності перешкоди на вході, система буде щонайкраще відтворювати вплив, що задає, x(t) і подавляти збурювання f(t). При наявності на вході високочастотної перешкоди частоту пропущення 
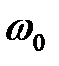системи вибирають також досить великою, але по компромісній умові спільної фільтрації всіх діючих сигналів.
Рисунок 1. АЧХ замкнутої системи
Настроювання системи за критерієм МО забезпечують мале перерегулювання й досить швидке протікання перехідного процесу з наступними показниками якості:
, 
, 
.
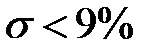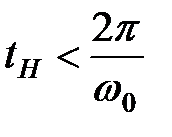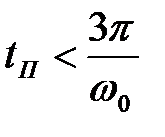Амплітудну характеристику, близьку за формою до прямокутної характеристики ідеального фільтра, має так званий фільтр Баттерворта, у якого АЧХ
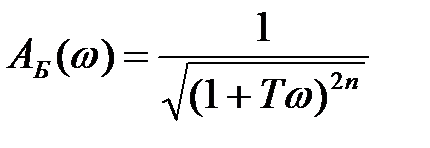. (1)
На практиці звичайно використовують фільтри з порядком п = 2...8.
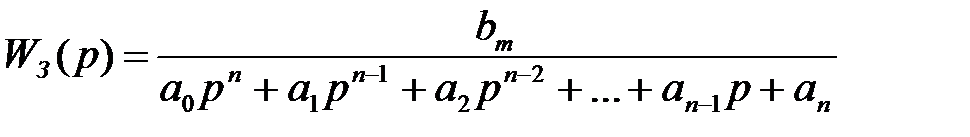(2)
приводять до нормованого виду
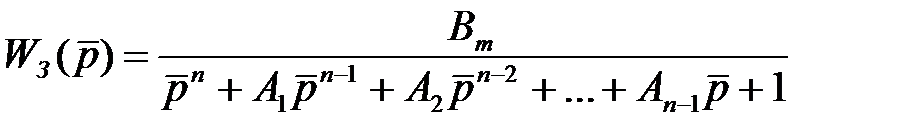, (3)
де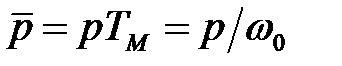 
- оператор Лапласа, що відповідає безрозмірному (відносному) часу 
, 
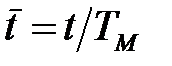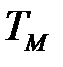- масштабний множник, рівний
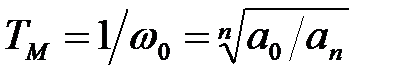; (4)
безрозмірні коефіцієнти
; 
;…; 
; 
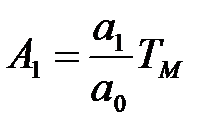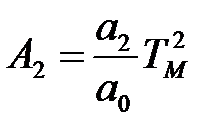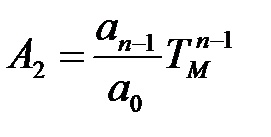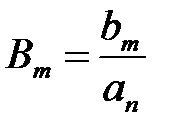... (5)
Щоб забезпечити бажану форму амплітудної характеристики, близьку до прямокутного, коефіцієнти нормованої функції (3) вибирають у відповідності зі стандартними поліномами Баттерворта (табл. 1). Саме при таких сполученнях коефіцієнтів Ai амплітудна характеристика фільтра приймає вид (1), причому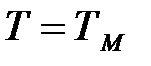 
, а відносна частота 
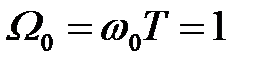відповідає значенню АЧХ, рівному 0,7 (при Вт = 1).
Таблиця 1. Коефіцієнти фільтрів Баттерворта
| n | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
| 1,4 | -- | -- | -- | -- | -- | -- | |
| 2,0 | 2,0 | -- | -- | -- | -- | -- | |
| 2,61 | 3,41 | 2,61 | -- | -- | -- | -- | |
| 3,24 | 5,24 | 5,24 | 3,24 | -- | -- | -- | |
| 3,86 | 7,46 | 9,13 | 7,46 | 3,86 | -- | -- | |
| 4,5 | 10,1 | 14,6 | 14,6 | 10,1 | 4,5 | -- | |
| 5,12 | 13,1 | 21,8 | 25,7 | 21,8 | 13,1 | 5,12 |
Масштабний множник ТМ не впливає на форму перехідного процесу й служить узагальненою мірою швидкодії системи. Його значення можна вибрати виходячи з необхідних показників швидкодії tH і tП по наступних наближених формулах:
, 
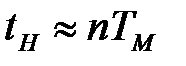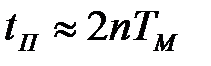. (6)
Знайдене по цих формулах значення ТМ забезпечують за рахунок вибору по формулі (4) відповідного загального передатного коефіцієнта розімкнутого контуру k, що входить у вільний член ап: ап = 1 + k - для статичних систем, ап = k - для астатических систем.
У системах, параметри яких обрані у відповідності зі стандартними поліномами Баттерворта, перерегулювання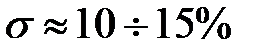 
.
Зазначені вище значення тривалості перехідного процесу tп і перерегулювання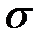 
строго витримуються тільки в тих випадках, коли чисельник передатної функції (2) не містить доданків з оператором р. Проте й для систем з більше складним поліномом чисельника можна користуватися значеннями коефіцієнтів Баттерворта, що рекомендуються. При цьому також забезпечується досить гарна якість перехідного процесу. Крім того, настроювання, що відповідають поліномам Баттерворта, можуть використовуватися як вихідні (відправні) для відшукання оптимальних настроювань систем, передатні функції яких мають чисельник у вигляді полінома від р.