Ix. билинейные и квадратичные формы
Линейные формы
Пусть Ln – n-мерное линейное пространство над полем Р и f –линейное отображение пространства Lnв поле Р (f : Ln® Р).
Определение 58. Линейное отображение f : Ln ® Р называется линейной функцией или линейной формой, заданной на Ln .
Если е = (е1, е2,... , еn) – базис в Ln , а – любой вектор из Ln , то а = х1е1 + х2е2 + … + хnеn, где х1, х2, … , хn – любые элементы поля Р. Если f (ек) = aк , то f (а) = a1х1 + a2х2+ … + anхn .
Следовательно, любую линейную форму можно задать в виде a1х1 + a2х2+ … + anхn .
Легко показать, что множество всех линейных форм f : Ln ® Р является линейным пространством над полем Р.
Билинейные формы
Пусть Ln – n-мерное линейное пространство над полем Р .
Определение 59. Отображение f : (Ln ´ Ln ) ® Р называется билинейной формой (или билинейной функцией), заданной на Ln , если для любых векторов а, в, с и любого элемента aÎ Р выполняются условия:
f (а + в, с) = f (а, с) + f (в, с) ; f (а, в + с ) = f (а, в) + f (а, с); f (a×а) = a×f(а).
(Иными словами, билинейная форма линейна по обоим переменным.)
Пусть в Ln зафиксирован базис е = (е1, е2,... , еn), а = х1е1 + х2е2 + … + хnеn,
в = у1е1 + у2е2 + … + уnеn, f (ек , ер) = aкр . Тогда из определения 58 следует
f (а, в) = f ( 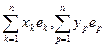 ) =
) = 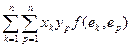 =
= 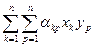 , где aкр – элементы поля Р.
, где aкр – элементы поля Р.
Итак, f (а, в) = 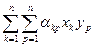 (55) – запись билинейной формы в координатах.
(55) – запись билинейной формы в координатах.
Матрица А = 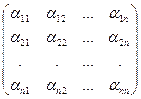 | называется матрицей данной билинейной формы. Если х и у – столбцы координат векторов а и в, то билинейную форму можно записать в матричном виде: f (а, в) = хТ× А × у (56) |
Если е1 = (е11, е21,... , еn1) – другой базис в Ln и Т – матрица перехода от базиса е к базису е1, то столбцы координат векторов а и в в этих базисах связаны формулами х = Т×х1, у =Т×у1. Подставив в формулу (56), получим f (а, в) = (Тх1)Т× А × (Ту1) = (х1)Т×(ТТ×А×Т)×у1. Следовательно, матрицы билинейной формы в разных базисах связаны формулой
А1 = ТТ×А×Т (57)
Определение 60. Билинейная форма называется симметрической, если
f (а, в) = f ( в, а) для любых векторов а и в. (57)
Очевидно, верно следующее утверждение:
Теорема 62. Билинейная форма является симметрической тогда и только тогда, когда она в любом базисе имеет симметрическую матрицу.
Теорема 63. В любом базисе евклидова пространства Еn скалярное произведение векторов задаётся симметрической билинейной формой.
Доказательство. По формуле (42) скалярное произведение векторов а и в равно
(а, в)= х Т×Г×у. Матрица Г – симметрическая, поэтому, согласно формуле (56), скалярное произведение задано симметрической билинейной формой.
Квадратичные формы
Пусть Ln – n-мерное линейное пространство над полем Р и пусть на нём задана симметрическая билинейная форма f (а, в).
Определение 61. Симметрическая билинейная форма f (а, в) при условии а = в называется квадратичной формой, заданной на Ln (j(а) = f(а, в) ). При этом f(а, в) и j(а) называются соответствующими друг другу.
Если в пространстве Ln задан базис е = (е1, е2,… , еn) и а = х1е1 + х2е2 + … + хnеn, то, используя формулу (55), получим запись квадратичной формы в координатах
j(а) = 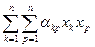 (59)
(59)
Матрица квадратичной формы совпадает с матрицей соответствующей симметрической билинейной формы. Квадратичная форма в матричном виде запишется
j(а) = хТ× А ×х (60)
Если в пространстве Ln зафиксирован базис, то между всеми квадратичными формами, заданными на Ln и всеми симметрическими квадратными матрицами порядка n устанавливается взаимнооднозначное соответствие. Сумма двух квадратичных форм является квадратичной формой. При умножении квадратичной формы на элемент поля Р получается тоже квадратичная форма. При сложении квадратичных форм складываются их матрицы. Если форма умножается на элемент поля Р, то на этот же элемент умножается и её матрица. Следовательно, множество всех квадратичных форм, заданных на Ln , есть линейное пространство, изоморфное линейному пространству квадратных симметрических матриц порядка n. Размерность этого пространства равна 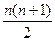 .
.
Так как квадратичная форма и соответствующая симметрическая билинейная форма имеют одну и ту же матрицу, то связь матриц А и А1 в разных базисах задаётся формулой (56), т.е. А1 = ТТ×А×Т , где Т – матрица перехода от первого базиса ко второму, ТТ – матрица, транспонированная для матрицы Т. Следовательно, в разных базисах квадратичная форма имеет более или менее сложные матрицы, а поэтому более или менее сложную запись в координатах. Поэтому возникает задача: найти в пространстве Ln такой базис, в котором квадратичная форма имела бы наиболее простой вид.
Определение 62. Если j(а) = a1х12 + a2х22 + … + an хn2, то говорят, что квадратичная форма j(а) имеет канонический вид.
Если поле Р есть поле рациональных или действительных чисел и
j(а) = х12 + х22 + … + хк2 – хк+12 – … – хr2,
то говорят, что квадратичная форма имеет нормальный вид. В случае, когда Р = Снормальным видом квадратичной формы называют j(а) = х12 + х22 + …+ хк2 + хк+12 + .+ хr2.
Теорема 64. Всякая квадратичная форма с помощью линейного невырожденного преобразования (преобразования координат) может быть приведена к каноническому виду.
Доказательство. Пусть j(а) – квадратичная форма, заданная на пространстве Ln . Пусть в Ln задан базис е и пусть в этом базисе j(а) = хТ× А ×х . Матрица А –симметрическая, поэтому по теореме 60 существует такая ортогональная матрица Т, что матрица А1 = Т–1×А×Т будет диагональной, причём на диагонали стоят собственные значения матрицы А (они все – действительные числа). Так как ортогональная матрица невырожденная, то существует такой базис е1, что Т будет матрицей перехода от базиса е к базису е1. Так как для ортогональной матрицы Т –1 = Т Т, то А1 – матрица данной формы в базисе е1. Итак, в базисе е1 данная форма имеет канонический вид.
Замечание. Приведение симметрической матрицы к диагональному виду описано в примере пункта 8.3.
Теорема 65.Всякую квадратичную форму линейным невырожденным преобразованием можно привести к нормальному виду.
Доказательство. В теореме 64 доказано, что квадратичную форму можно привести к каноническому виду. Перенумеровав, если нужно переменные, будем считать, что первые r коэффициентов в каноническом виде отличны от нуля, а остальные (n – r) равны нулю.
1) В случае, когда Р = С сделаем преобразование координат по формулам (*).
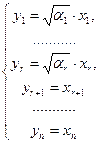 (*) (*) | Так как определитель этих формул отличен от нуля, то они задают преобразование координат. В новых координатах j(а) = у12 + у22 + … + уr2. Получили комплексный нормальный вид квадратичной формы. 2) Если Р = R , т.е. j(а) – действительная квадратичная форма, то в каноническом виде запишем сначала члены с положительными коэффициентами, затем – с отрицательными и, наконец, с нулевыми. |
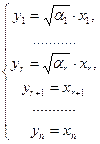 (**) (**) | j(а) = a1х12 + a2х22 + … + aк хк2 – aк+1хк+12 – … – arхr2 Сделаем преобразование координат по формулам (**), получим j(а) = у12 + у22 + … + ук2 – ук+12 – … – уr2 . Но это и есть нормальный вид действительной квадратичной формы. |
Пример. Привести к каноническому виду квадратичную форму
j = 2х1х2 + 2х1х3 – 2х1х4 – 2х2х3 + 2х2х4 + 2х3х4 .
Решение. Матрица данной квадратичной формы
А = 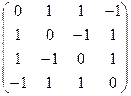 | Для решения задачи эту матрицу нужно привести к диагональному виду. Это было сделано в примере пункта 8.3. Собственные значения этой матрицы l1 = l2 = l3 = 1, l4 = – 3. Базис из собственных векторов был найден е11 = 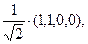 е21 = е21 = 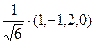 , , |
А1 = 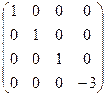 | е31 = 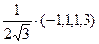 , е41 = , е41 = 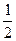 (1, –1, –1, 1). В этом базисе квадратичная форма будет иметь матрицу А1. Матрицей перехода от исходного базиса к базису е1 будет матрица Т. (1, –1, –1, 1). В этом базисе квадратичная форма будет иметь матрицу А1. Матрицей перехода от исходного базиса к базису е1 будет матрица Т. |
Т = 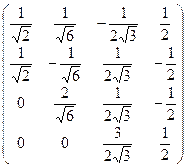 | Следовательно, форма j будет иметь следующий канонический вид j = х12 + х22 + х32 – 3х42. |
