Вынужденные колебания механической системы с одной степенью свободы без сопротивления.
Q(t) - обобщенная сила характеризующая внешнее воздействие на колебательную систему. 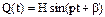 , где: H - амплитуда, p - циклическая (круговая) частота,
, где: H - амплитуда, p - циклическая (круговая) частота, 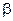 - начальная фаза обобщенной силы. Определяем положение системы обобщенной координатой q, при равновесии
- начальная фаза обобщенной силы. Определяем положение системы обобщенной координатой q, при равновесии 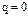 Уравнение Лагранжа II рода:
Уравнение Лагранжа II рода: 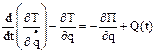 (1). Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями:
(1). Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями: 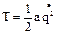 ,
, 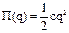 . Находим:
. Находим: 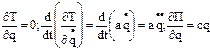 (2). Подставляя (2) в (1), получим:
(2). Подставляя (2) в (1), получим: 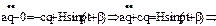
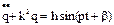 , где:
, где: 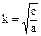 = const, круговая или циклическая частота собственных колебаний системы,
= const, круговая или циклическая частота собственных колебаний системы, 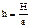 = const.
= const. 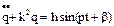 - НЛДУ II порядка с постоянными коэффициентами (1). Решение q(t) это сумма общего решения
- НЛДУ II порядка с постоянными коэффициентами (1). Решение q(t) это сумма общего решения 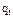 однородного уравнения и частного решения
однородного уравнения и частного решения 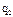 неоднородного уравнения, то есть:
неоднородного уравнения, то есть: 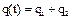 . Однородное уравнение для определения
. Однородное уравнение для определения 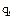 это уравнениее собственных колебаний, его решение:
это уравнениее собственных колебаний, его решение: 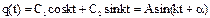 . Частное решение
. Частное решение 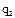 неоднородного уравнения называют вынужденными колебаниями системы. Оно зависит от соотношения круговых частот «k» и «p» свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса (
неоднородного уравнения называют вынужденными колебаниями системы. Оно зависит от соотношения круговых частот «k» и «p» свободных колебаний и возмущающей силы. Здесь возможны два случая: отсутствие резонанса ( 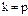 ) и резонанс (
) и резонанс ( 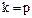 ). k≠p
). k≠p 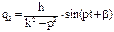 - частное решение (1) Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1):
- частное решение (1) Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1): 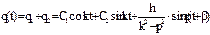 , или в амплитудной форме
, или в амплитудной форме 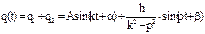 Постоянные
Постоянные 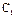 и
и 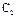 определяются из начальных условий:
определяются из начальных условий: 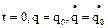 .k=p
.k=p 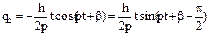 - частное решение (1) Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1):
- частное решение (1) Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1): 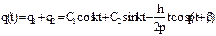 , или в амплитудной форме:
, или в амплитудной форме: 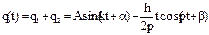 . Постоянные
. Постоянные 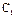 и
и 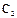 определяются из начальных условий:
определяются из начальных условий: 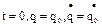 .
.
18)Свободные колебания механической системы с двумя степенями свободы без сопротивления.
В частном случае системы с двумя степенями свободы квадратичные формы Т, П, Ф будут соответственно равны 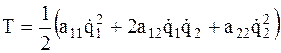 ; (4.1)
; (4.1) 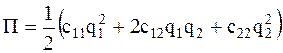 ; (4.2)
; (4.2) 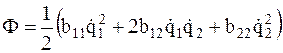 , (4.3) а дифференциальные уравнения малых колебаний примут вид
, (4.3) а дифференциальные уравнения малых колебаний примут вид 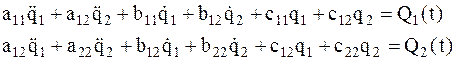 (4.4) Рассмотрим свободные колебания консервативной системы. В этом случае
(4.4) Рассмотрим свободные колебания консервативной системы. В этом случае 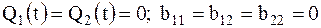 и дифференциальные уравнения принимают вид:
и дифференциальные уравнения принимают вид: 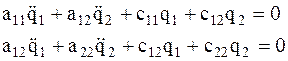 (4.5) Начальные условия для
(4.5) Начальные условия для 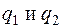 имеют вид:
имеют вид: 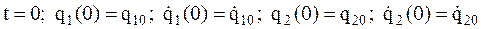 (4.6) В силу положительной определенности квадратичной формы кинетической энергии обобщенные инерционные коэффициенты удовлетворяют соотношениям
(4.6) В силу положительной определенности квадратичной формы кинетической энергии обобщенные инерционные коэффициенты удовлетворяют соотношениям 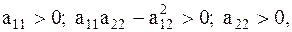 а аналогичные соотношения для квазиупругих коэффициентов
а аналогичные соотношения для квазиупругих коэффициентов 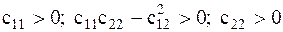 являются достаточными условиями устойчивости положения равновесия системы. Коэффициенты
являются достаточными условиями устойчивости положения равновесия системы. Коэффициенты 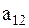 и
и 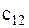 , связывающие в уравнениях (4.5) обобщенные координаты
, связывающие в уравнениях (4.5) обобщенные координаты 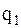 и
и 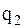 , называют соответственно коэффициентами инерционной и упругой связи. Если в колебательной системе коэффициент
, называют соответственно коэффициентами инерционной и упругой связи. Если в колебательной системе коэффициент 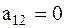 , ее называют системой с упругой связью, а если
, ее называют системой с упругой связью, а если 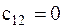 – системой с инерционной связью. Парциальной системой, соответствующей обобщенной координате
– системой с инерционной связью. Парциальной системой, соответствующей обобщенной координате 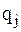 , называют условную колебательную систему с одной степенью свободы, получаемую из исходной системы, если наложить запрет на изменение всех обобщенных координат, кроме
, называют условную колебательную систему с одной степенью свободы, получаемую из исходной системы, если наложить запрет на изменение всех обобщенных координат, кроме 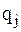 . Парциальными частотами называют собственные частоты
. Парциальными частотами называют собственные частоты 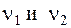 парциальных систем:
парциальных систем: 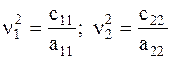 . (4.7) Поскольку уравнения (4.5) содержат только обобщенные координаты и их вторые производные по времени, ищем их решение в виде
. (4.7) Поскольку уравнения (4.5) содержат только обобщенные координаты и их вторые производные по времени, ищем их решение в виде 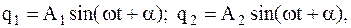 (4.8) где
(4.8) где 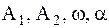 – пока неопределенные величины. Подставив (4.8) в (4.5) и приравняв коэффициенты при синусах, получим однородную алгебраическую систему относительно
– пока неопределенные величины. Подставив (4.8) в (4.5) и приравняв коэффициенты при синусах, получим однородную алгебраическую систему относительно 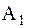 и А₂
и А₂ 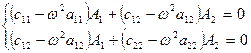 (4.9) Для того, чтобы однородная алгебраическая система (4.9) имела ненулевое решение, она должна быть вырожденной, т.е. ее определитель должен равняться нулю:
(4.9) Для того, чтобы однородная алгебраическая система (4.9) имела ненулевое решение, она должна быть вырожденной, т.е. ее определитель должен равняться нулю: 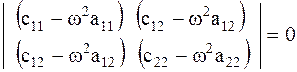 (4.10) Следовательно, решение (4.7) будет иметь смысл только при тех значениях
(4.10) Следовательно, решение (4.7) будет иметь смысл только при тех значениях 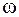 , которые удовлетворяют условию (4.9). Раскрывая (4.10), получаем
, которые удовлетворяют условию (4.9). Раскрывая (4.10), получаем 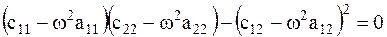 (4.11) или
(4.11) или 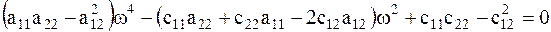 (4.12) Уравнение, представленное в форме (4.10), (4.11) или (4.12) называют частотным.Как видно из (4.12) частотное уравнение – биквадратное уравнение. Найденные из (4.10)–(4.12) значения
(4.12) Уравнение, представленное в форме (4.10), (4.11) или (4.12) называют частотным.Как видно из (4.12) частотное уравнение – биквадратное уравнение. Найденные из (4.10)–(4.12) значения 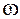 называют собственными частотами колебаний системы.Исследование корней частотного уравнения позволяет сделать следующие выводы: 1) если положение равновесия устойчивое, то оба корня частотного уравнения положительны; 2) первая собственная частота системы
называют собственными частотами колебаний системы.Исследование корней частотного уравнения позволяет сделать следующие выводы: 1) если положение равновесия устойчивое, то оба корня частотного уравнения положительны; 2) первая собственная частота системы 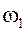
 всегда меньше меньшей парциальной частоты, а вторая
всегда меньше меньшей парциальной частоты, а вторая 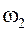 – больше большей парциальной частоты. Для колебательных систем с упругой связью (
– больше большей парциальной частоты. Для колебательных систем с упругой связью ( 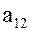 = 0) справедливо равенство
= 0) справедливо равенство 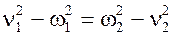 (4.13) Запишем два частных независимых решения, соответствующих частотам
(4.13) Запишем два частных независимых решения, соответствующих частотам 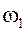 и
и 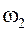 , в виде
, в виде 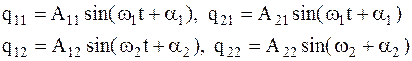 (4.14) где вторая цифра в индексе соответствует номеру частоты, или номеру тона колебаний.Константы
(4.14) где вторая цифра в индексе соответствует номеру частоты, или номеру тона колебаний.Константы 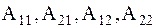 не являются независимыми, так как система (4.9) вырожденная. Коэффициенты связаны между собой соотношениями
не являются независимыми, так как система (4.9) вырожденная. Коэффициенты связаны между собой соотношениями 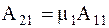 , где
, где 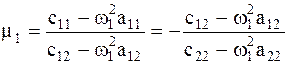 . (4.15)
. (4.15) 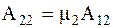 , где
, где 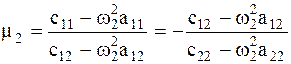 . (4.16) С учетом (4.15) и (4.16) частные решения (4.14) будут иметь вид
. (4.16) С учетом (4.15) и (4.16) частные решения (4.14) будут иметь вид 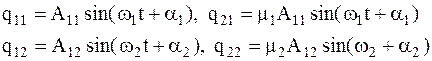 (4.17) Колебания, уравнения которых имеют вид (4.17) называют хлавными колебаниями. Они представляют собой гармонические колебания с частотами
(4.17) Колебания, уравнения которых имеют вид (4.17) называют хлавными колебаниями. Они представляют собой гармонические колебания с частотами 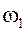 и
и 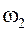 соответственно. Коэффициенты
соответственно. Коэффициенты 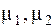 называют коэффициентами распределения амплитуд. Они характеризуют отношение амплитуд в главных колебаниях или форму главных колебаний. Коэффициенты распределения амплитуд и, следовательно, формы главных колебаний, как и собственные частоты, определяются параметрами самой колебательной системы и не зависят от начальных условий. Поэтому формы колебаний называют, так же как и частоты, собственными формами колебаний при колебаниях по соответствующему тону. Общее решение системы уравнений (4.5) может быть представлено как сумма найденных частных решений (4.17)
называют коэффициентами распределения амплитуд. Они характеризуют отношение амплитуд в главных колебаниях или форму главных колебаний. Коэффициенты распределения амплитуд и, следовательно, формы главных колебаний, как и собственные частоты, определяются параметрами самой колебательной системы и не зависят от начальных условий. Поэтому формы колебаний называют, так же как и частоты, собственными формами колебаний при колебаниях по соответствующему тону. Общее решение системы уравнений (4.5) может быть представлено как сумма найденных частных решений (4.17) 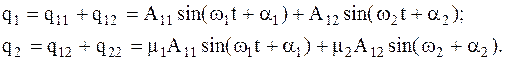 (4.18) Общее решение содержит четыре неопределенные постоянные
(4.18) Общее решение содержит четыре неопределенные постоянные 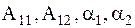 , которые должны определяться из начальных условий (4.6). При произвольных начальных условиях обе константы
, которые должны определяться из начальных условий (4.6). При произвольных начальных условиях обе константы 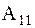 и
и 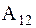 отличны от нуля. Это означает, что изменение во времени каждой обобщенной координаты будет представлять собой сумму хармонических колебаний с частотами
отличны от нуля. Это означает, что изменение во времени каждой обобщенной координаты будет представлять собой сумму хармонических колебаний с частотами 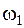 и
и 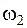 . А такие колебания являются не только не хармоническими, но в общем случае и не периодическими. Рассмотрим случай свободных колебаний системы, когда собственные частоты колебаний системы
. А такие колебания являются не только не хармоническими, но в общем случае и не периодическими. Рассмотрим случай свободных колебаний системы, когда собственные частоты колебаний системы 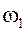 и
и 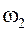 мало отличаются друг от друга:
мало отличаются друг от друга: 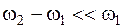 Обозначим
Обозначим 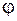 разность аргументов синусов в общем решении (4.18) уравнений свободных колебаний
разность аргументов синусов в общем решении (4.18) уравнений свободных колебаний 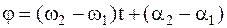 . (4.19) При
. (4.19) При 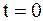 величина
величина 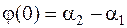 , а с возрастанием времени эта зависимость из-за малости
, а с возрастанием времени эта зависимость из-за малости 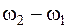 увеличивается очень медленно. Тогда
увеличивается очень медленно. Тогда 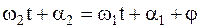 С учетом последнего равенства, общее решение уравнений свободных колебаний (4.18) может бытьт записано в виде:
С учетом последнего равенства, общее решение уравнений свободных колебаний (4.18) может бытьт записано в виде: 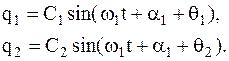 (4.20) В этих уравнениях
(4.20) В этих уравнениях 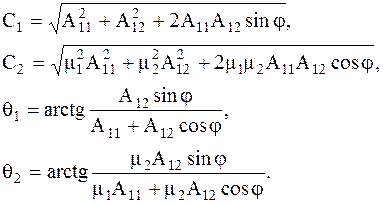 (4.21) Так как выражения (4.21) зависят от
(4.21) Так как выражения (4.21) зависят от 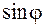 и
и 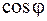 , а угол
, а угол 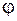 медленно изменяется с изменением времени, то рассматриваемые колебания (4.20) будут колебаниями с периодически изменяющейся амплитудой. Период изменения амплитуды в этом случае значительно больше периода колебаний (рис. 4.1). Если коэффициенты распределения амплитуд
медленно изменяется с изменением времени, то рассматриваемые колебания (4.20) будут колебаниями с периодически изменяющейся амплитудой. Период изменения амплитуды в этом случае значительно больше периода колебаний (рис. 4.1). Если коэффициенты распределения амплитуд 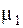 и
и 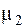 имеют разные знаки, то максимуму
имеют разные знаки, то максимуму 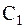 соответствует минимум
соответствует минимум 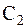 и наоборот. При усилении первого главного колебания интенсивность второго главного колебания уменьшается и наоборот, то есть энергия движения системы периодически оказывается как бы сосредоточенной то в одном, то в другом звене этой вибрирующей системы. Такое явление называют биением.Возможен другой подход к решению задачи о свободных колебаниях системы – найти какие-то новые обобщенные координаты
и наоборот. При усилении первого главного колебания интенсивность второго главного колебания уменьшается и наоборот, то есть энергия движения системы периодически оказывается как бы сосредоточенной то в одном, то в другом звене этой вибрирующей системы. Такое явление называют биением.Возможен другой подход к решению задачи о свободных колебаниях системы – найти какие-то новые обобщенные координаты 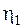 и
и 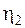 называемые нормальнымиили главными, для которых при любых начальных условиях движение будет одночастотным и хармоническим. Зависимость между обобщенными координатами
называемые нормальнымиили главными, для которых при любых начальных условиях движение будет одночастотным и хармоническим. Зависимость между обобщенными координатами 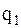 и
и 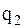 , выбранными произвольно, и главными координатами
, выбранными произвольно, и главными координатами 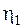 и
и 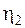 можно выразить так:
можно выразить так: 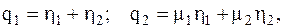 (4.22) где
(4.22) где 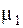 и
и 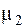 – коэффициенты распределения амплитуд (коэффициенты формы). Можно показать, что переход от исходных координат к главным приводит квадратичные формы кинетической и потенциальной энергии к каноническому виду:
– коэффициенты распределения амплитуд (коэффициенты формы). Можно показать, что переход от исходных координат к главным приводит квадратичные формы кинетической и потенциальной энергии к каноническому виду: 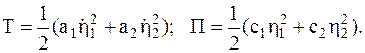
 (4.23) Здесь
(4.23) Здесь 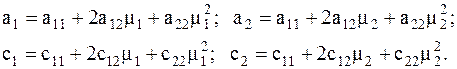 Подставив полученные для
Подставив полученные для 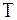 и
и 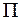 выражения (4.23) в уравнения Лагранжа второго рода, получим уравнения малых колебаний системы в главных координатах:
выражения (4.23) в уравнения Лагранжа второго рода, получим уравнения малых колебаний системы в главных координатах: 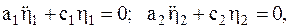 причем
причем 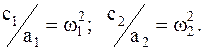 Выразив из системы (4.22)
Выразив из системы (4.22) 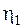 и
и 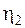 через
через 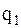 и
и 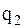 получим
получим

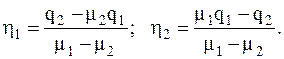 (4.24)Нормальные координаты находят широкое применение при решении задач о вынужденных колебаниях в случае произвольного возмущения, а также при решении задач о свободном движении в неконсервативных системах. Вопросы? Не слышу?
(4.24)Нормальные координаты находят широкое применение при решении задач о вынужденных колебаниях в случае произвольного возмущения, а также при решении задач о свободном движении в неконсервативных системах. Вопросы? Не слышу?
19)Вынужденные колебания механической системы с двумя степенями свободы без сопротивления. Не проходили:D
