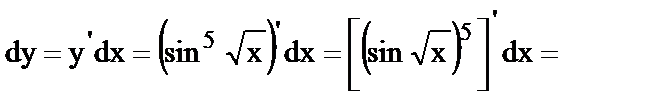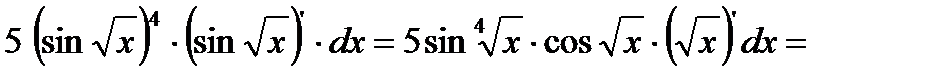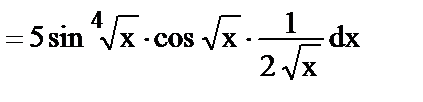Тема 2.2. Дифференциальное исчисление
Понятие производной функции и ее геометрический смысл.
Производные обратной и сложной функции.
Правила и формулы дифференцирования.
Приложения производной функции.
Пункт 1. Понятие производной функции и ее геометрический смысл.
Пусть функция 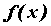 определена на промежутке
определена на промежутке 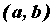 . Точка
. Точка 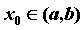 - произвольная точка из области определения функции,
- произвольная точка из области определения функции, 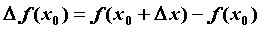 - приращение функции в точке
- приращение функции в точке 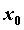 , вызванное приращением
, вызванное приращением 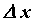 независимой переменной
независимой переменной 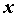 .
.
Производной функции 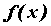 по независимой переменной
по независимой переменной 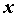 в точке
в точке 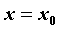 ,
, 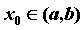 называется предел отношения приращения функции
называется предел отношения приращения функции 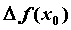 к приращению
к приращению 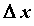 при стремлении
при стремлении 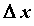 к нулю, т.е.
к нулю, т.е.
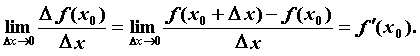
Обозначение: 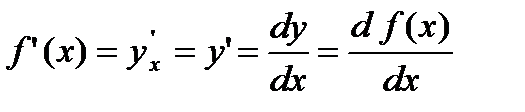
Дифференцирование - операция нахождения производной.
Чтобы вычислить производную функции в точке хо, нужно в общее выражение производной вместо независимой переменной х подставить числовое значение
х = хо, т.е. вычислит значение f’(xo). Таким образом, производная в данной точке хо есть число.
Геометрический смысл производной: Угловой коэффициент касательной равен значению производной в точке 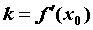 и ее уравнение имеет вид
и ее уравнение имеет вид 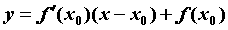 .
.
Пусть функция 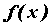 определена в некоторой окрестности точки
определена в некоторой окрестности точки 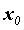 . Рассмотрим приращение функции в этой точке:
. Рассмотрим приращение функции в этой точке: 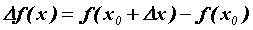 . Функция
. Функция 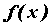 называется дифференцируемой в точке, если ее приращение можно записать в виде
называется дифференцируемой в точке, если ее приращение можно записать в виде 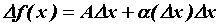 , где
, где 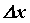 - приращение независимой переменной,
- приращение независимой переменной,
А – постоянная, не зависящая от 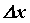 ,
, 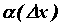 - бесконечно малая функция при
- бесконечно малая функция при 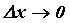 .
.
Дифференциалом функции 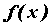 в точке
в точке 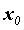 называется линейная по
называется линейная по 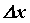 часть
часть 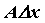 приращения
приращения 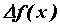 . Дифференциал обозначается
. Дифференциал обозначается 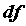 , то есть
, то есть 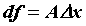 .
.
Другими словами, дифференциал функции выражается формулой 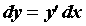 .
.
Производной второго порядка от функции 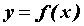 называется производная от ее производной:
называется производная от ее производной: 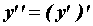 . Аналогично определяют производную любого порядка:
. Аналогично определяют производную любого порядка: 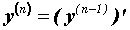 .
.
Пункт 2. Производные обратной и сложной функций.
Пусть 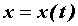 - функция, дифференцируемая в точке
- функция, дифференцируемая в точке 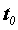 ,
, 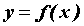 - функция, дифференцируемая в точке
- функция, дифференцируемая в точке 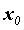 , причем
, причем 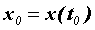 . Тогда
. Тогда 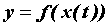 - сложная функция независимого переменного
- сложная функция независимого переменного 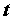 , дифференцируема в точке
, дифференцируема в точке 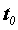 и ее производная в этой точке вычисляется по формуле
и ее производная в этой точке вычисляется по формуле 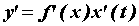 .
.
Обычно 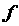 называют внешней функцией, а
называют внешней функцией, а 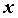 - внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.
- внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.
Пусть функция 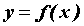 дифференцируема и строго монотонна на
дифференцируема и строго монотонна на 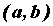 . Пусть также в точке
. Пусть также в точке 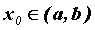 производная
производная 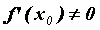 . Тогда в точке
. Тогда в точке 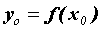 определена дифференцируемая функция
определена дифференцируемая функция 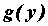 , которую называют обратной к
, которую называют обратной к 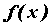 , а ее производная вычисляется по формуле
, а ее производная вычисляется по формуле 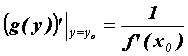 .
.
Пункт 3. Правила и формулы дифференцирования.
Правила дифференцирования
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) ' = 0,
2) (cu) ' = cu';
3) (u+v)' = u'+v';
4) (uv)' = u'v+v'u;
5) (u/v)' = (u'v-v'u)/v2;
Формулы дифференцирования
1. (un)' = n un-1 u'
2. (au)' = au lna u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u u'.
7. (cos u)' = - sin u u'.
8. (tg u)' = 1/ cos2u u'.
9. (ctg u)' = - u' / sin2u.
10. (arcsin u)' = u' / 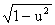 .
.
11. (arccos u)' = - u' / 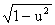 .
.
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
Примеры:
Вычислите производную функции.
1. 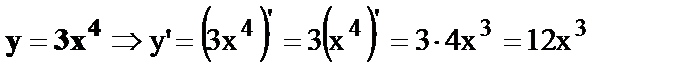 .
.
2. 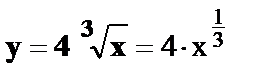
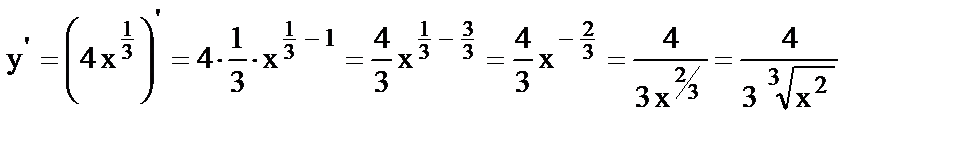 .
.
3. 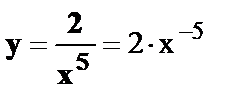
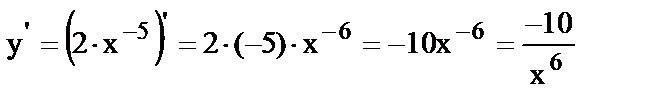 .
.
4. 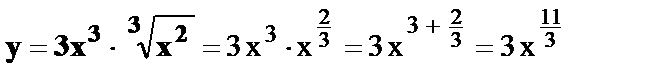
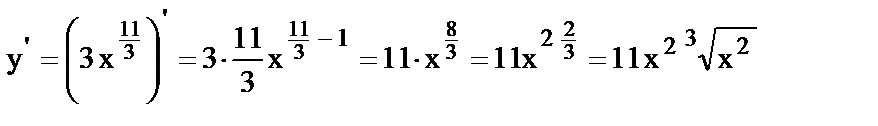 .
.
5. 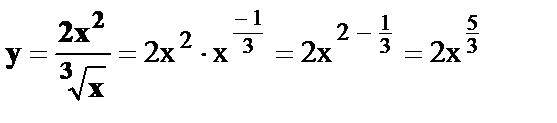
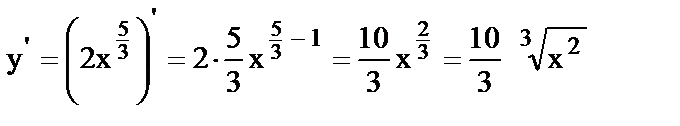 .
.
6. 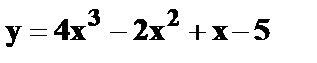
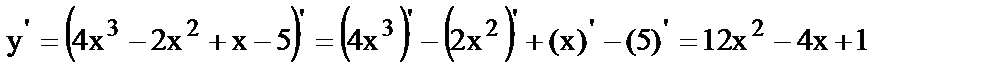 .
.
7. 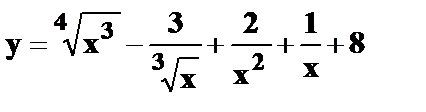
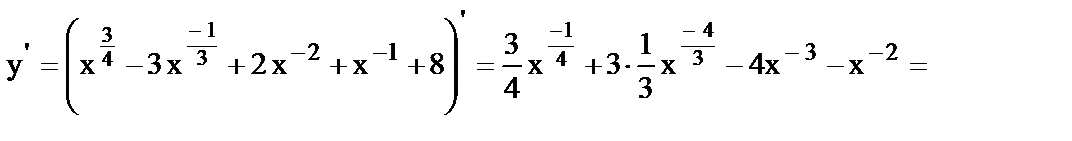
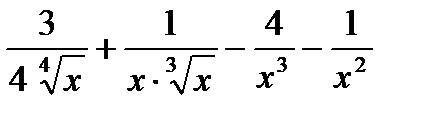
8. 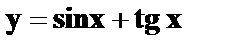
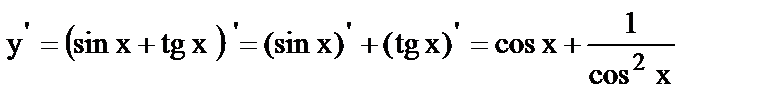
9. 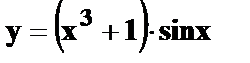
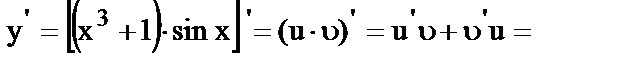
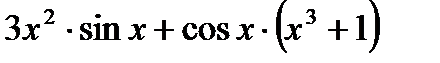
10. 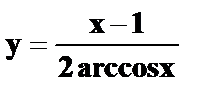
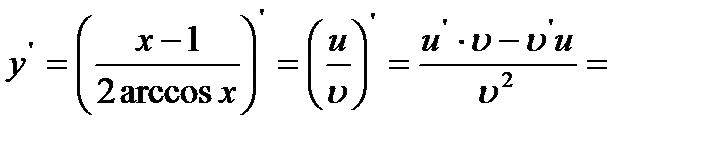
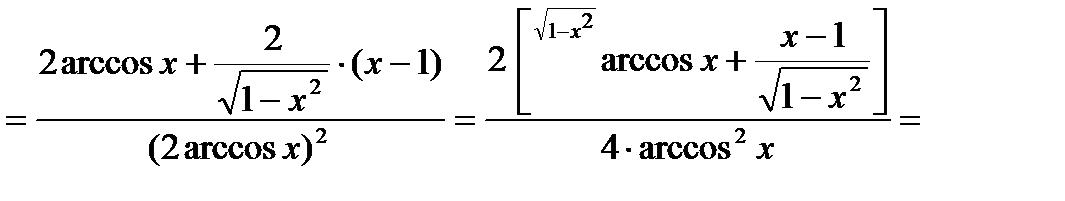
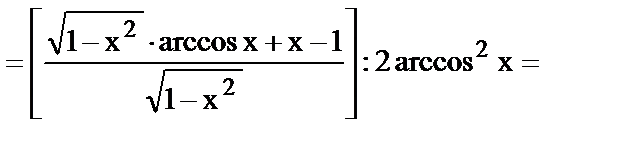
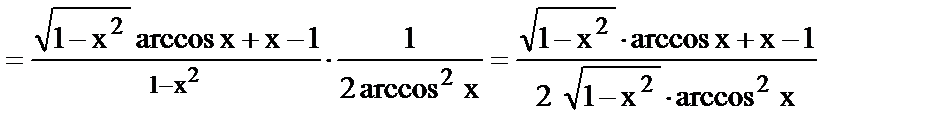 .
.
Вычислите производную сложной функции.
11. 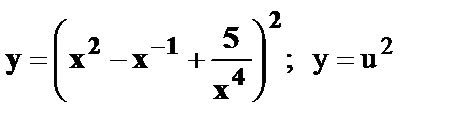 , где
, где 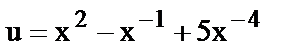 .
.
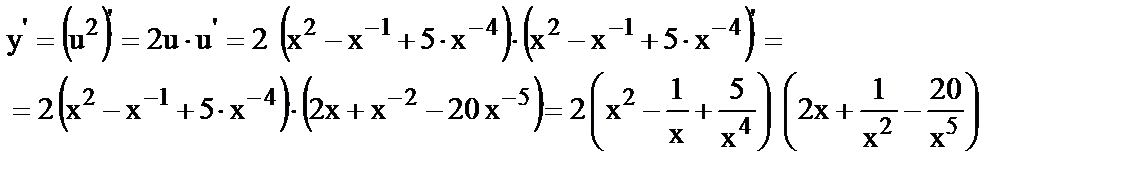
12. 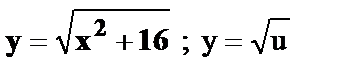 , где
, где 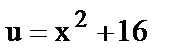 .
.
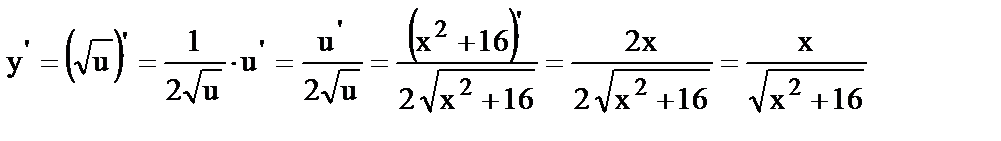
13. 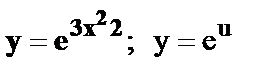 , где
, где 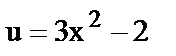 .
.
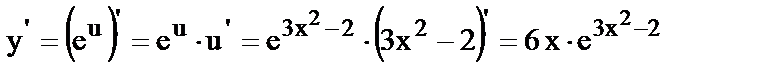
14. 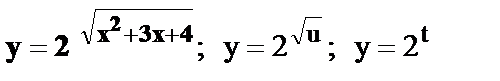 , где
, где 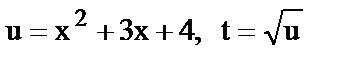 .
.
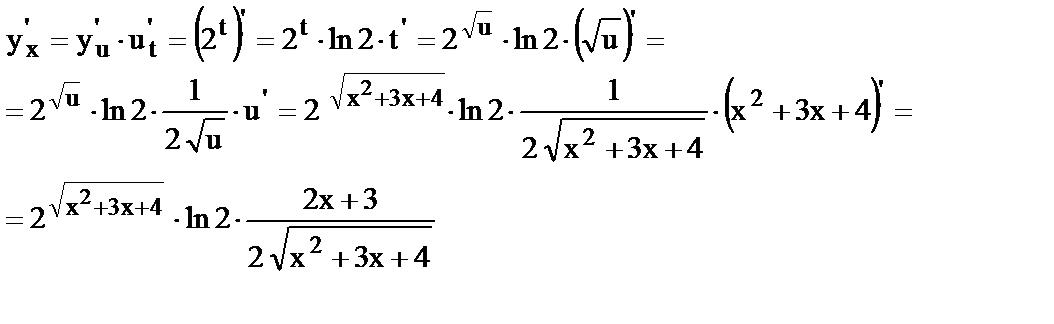
15. 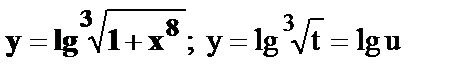 , где
, где 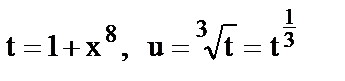 .
.
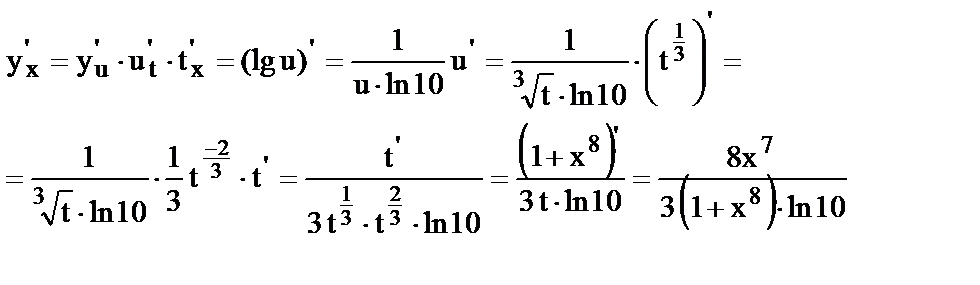
16. 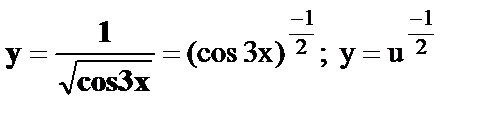 , где
, где 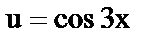 .
.
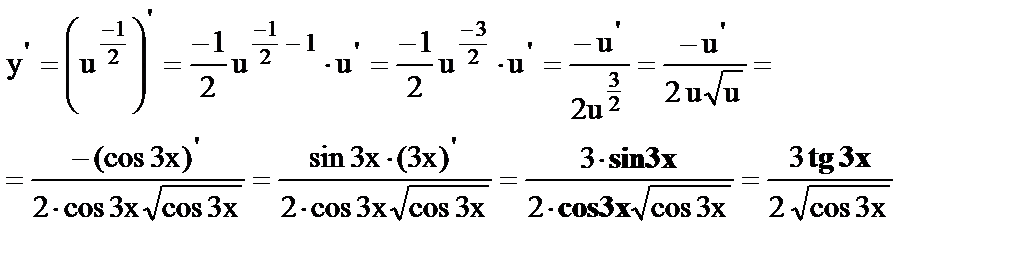
17. 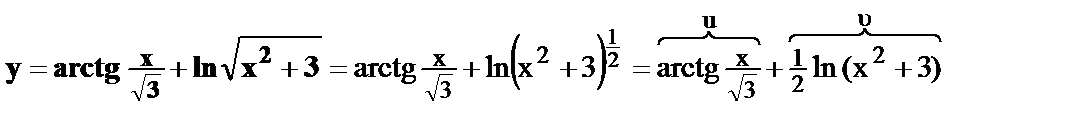
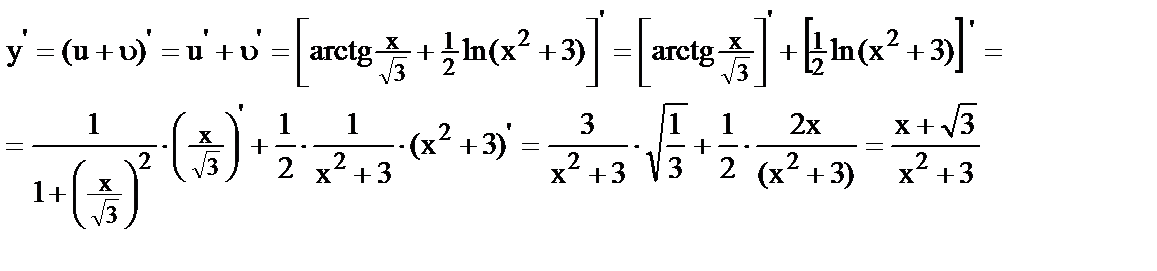
18. 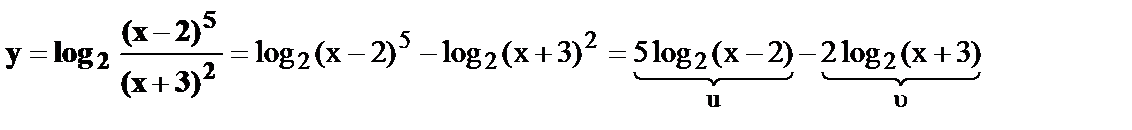
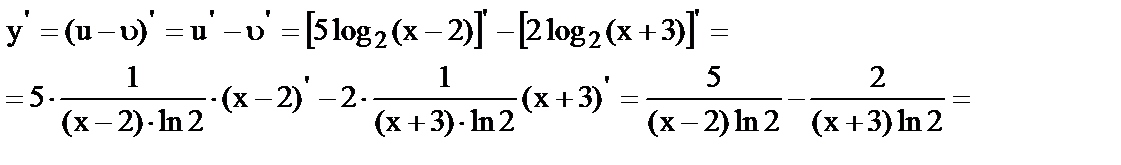
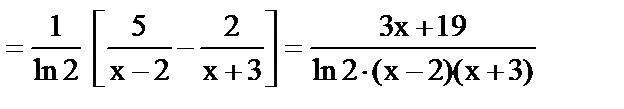
19. 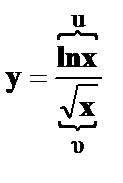
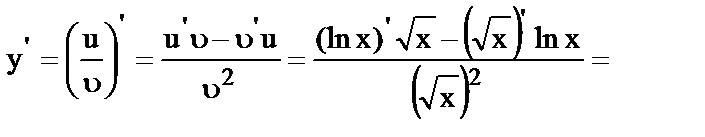
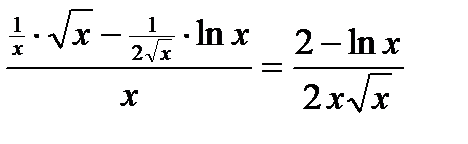
20. 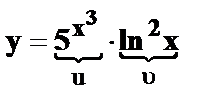
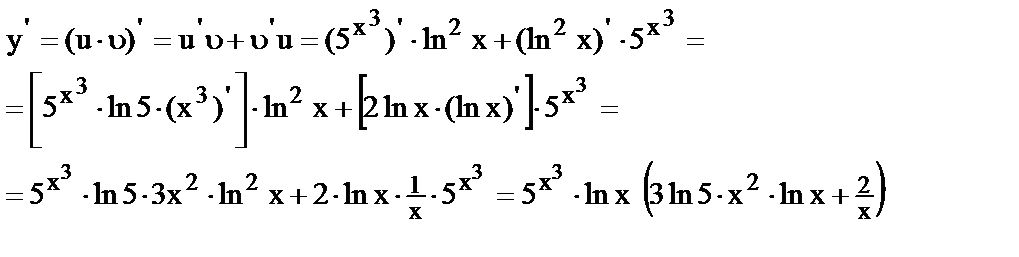
Вычислить вторую производную функции.
21. 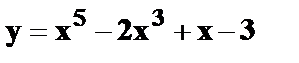
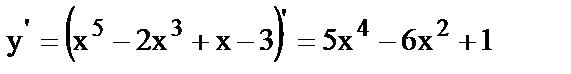
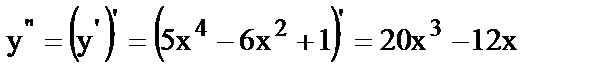
22. 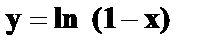
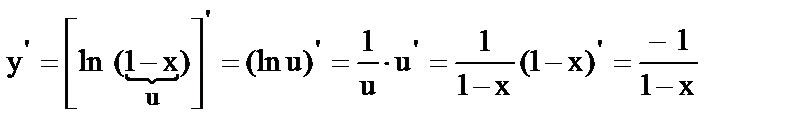
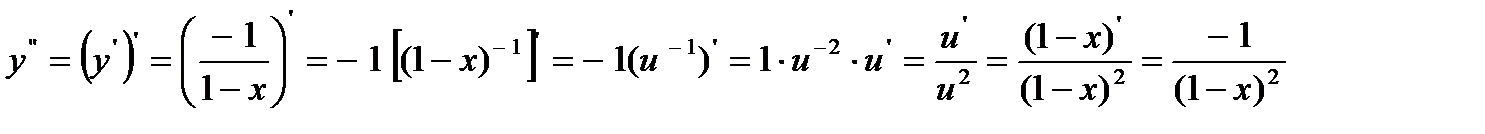
23. 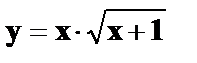
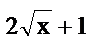 |
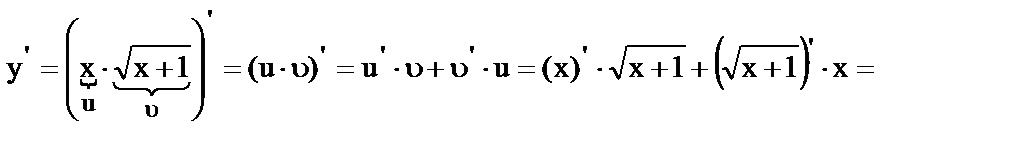
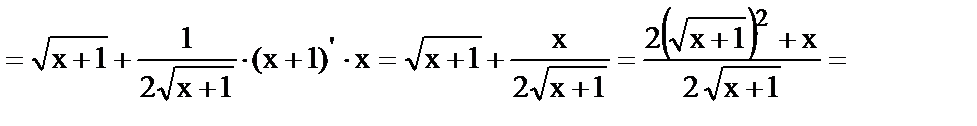
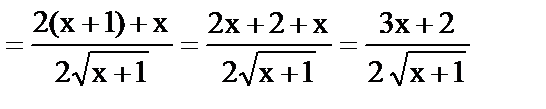
. 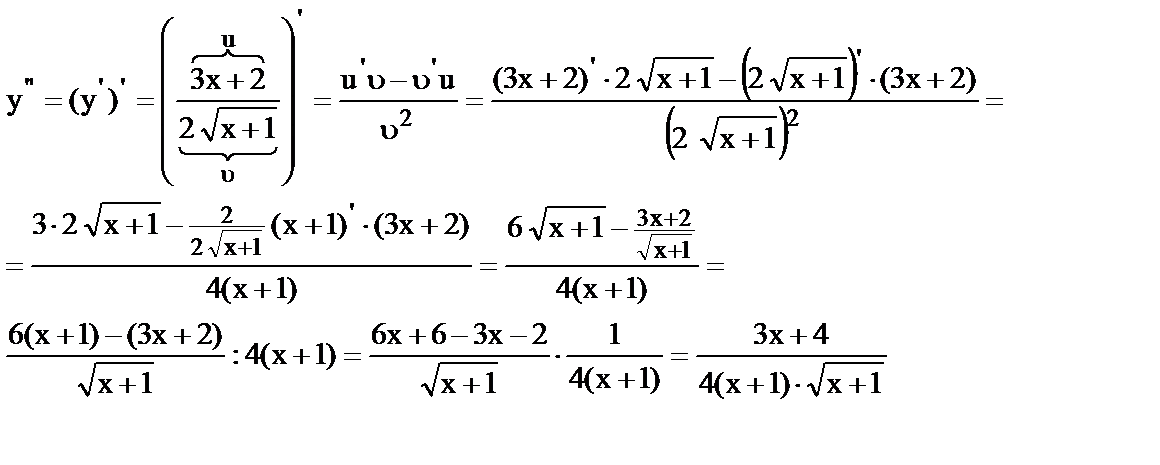
Вычислить дифференциал функции.
24. 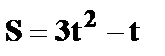 ;
; 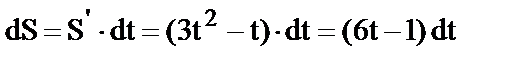 .
.
25. 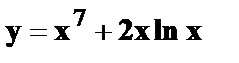
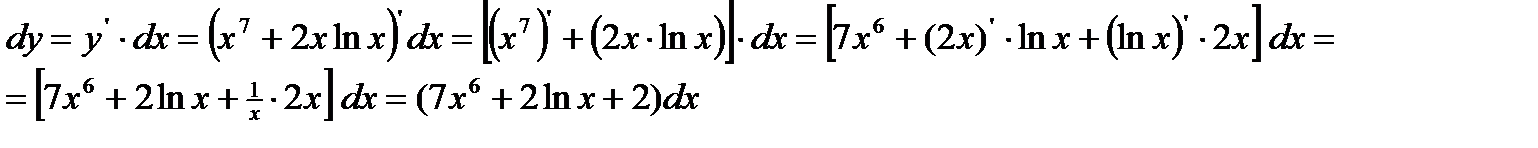
26. 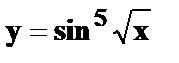 ;
;