Пределы и непрерывность
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Методические указания
К выполнению индивидуальных заданий
по теме:
Пределы, непрерывность.
Производные»
Волгодонск
Пределы и непрерывность
Отметим некоторые теоремы о пределах, которые часто применяются для решения задач.
Если существуют конечные пределы 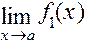 и
и 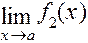 , то
, то
1) 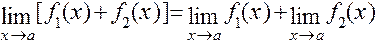 ;
;
2) 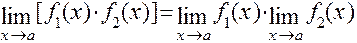 ;
;
3) 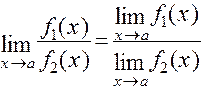 ( если
( если 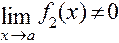 ).
).
Отметим еще два замечательных предела и следствия из них:
1) 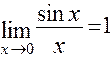 ;
;
2) 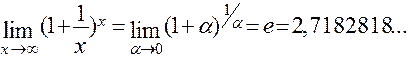 ;
;
3) 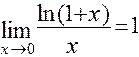 ; 4)
; 4) 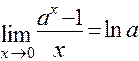 ; 5)
; 5) 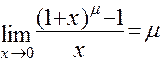 .
.
Задача 1. Найти указанные пределы, не пользуясь правилом Лопиталя:
а) 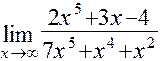 ; г)
; г) 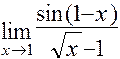 ;
;
б) 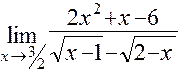 ; д)
; д) 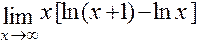 ;
;
в) 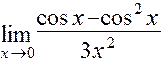 ; е)
; е) 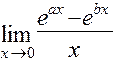 ; ж)
; ж) 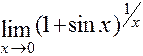 ;
;
з) 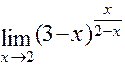 ; и)
; и) 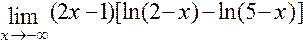 ;
;
к) 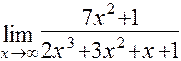 ; л)
; л) 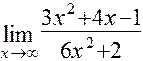 ; м)
; м) 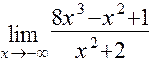 .
.
Очевидно, что в каждой из перечисленных задач нельзя непосредственно применить теоремы 1-3.
Решение. а) Если 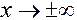 , то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на
, то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на 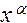 , где
, где 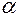 - степень многочлена, стоящего в знаменателе:
- степень многочлена, стоящего в знаменателе: 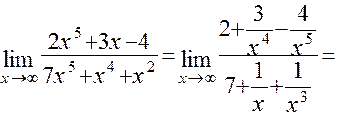
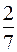 .
.
Здесь мы воспользовались равенством 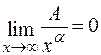 при
при 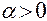 .
.
б) Прежде чем решать эту задачу, отметим, что если два многочлена 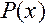 и
и 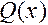 обращаются в нуль при
обращаются в нуль при 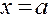 , т.е.
, т.е. 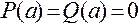 , то они представляются в виде
, то они представляются в виде
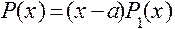 и
и 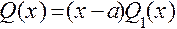 .
.
И тогда
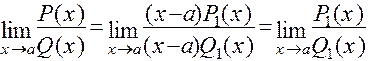 и т.д.
и т.д.
Постараемся свести нашу задачу к указанному случаю предела частного двух многочленов, для чего и числитель, и знаменатель дроби, стоящей под знаком предела, умножим на 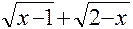 , избавившись тем самым от иррациональности в знаменателе. Итак,
, избавившись тем самым от иррациональности в знаменателе. Итак,
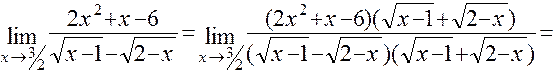
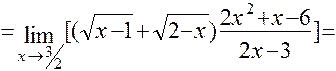
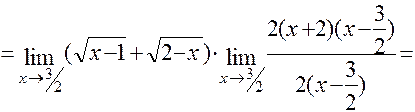
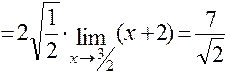 .
.
в) Для решения этой задачи воспользуемся первым замечательным пределом:
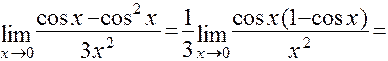
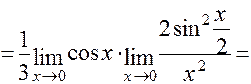
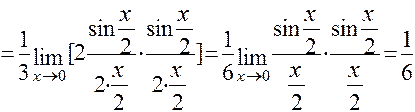
(Так как 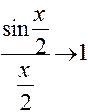 при
при 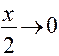 ).
).
г) Для решения данной задачи воспользуемся вторым замечательным пределом:
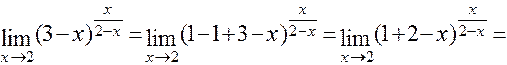
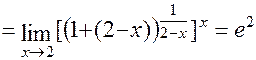 .
.
Последнее равенство вытекает из того, что в квадратной скобке стоит 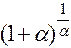 , где
, где 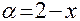 .
.
д) Для решения этой задачи применим первое следствие из второго замечательного предела:
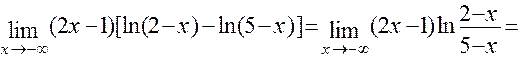
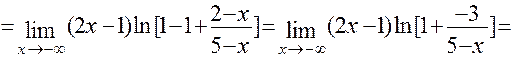
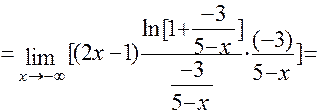
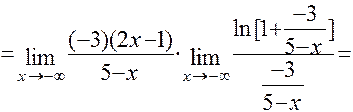
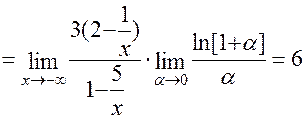 ( Здесь
( Здесь 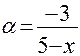 ).
).
Решения задач е, ж аналогичны решению задачи а.
Например, задача ж имеет следующее решение: 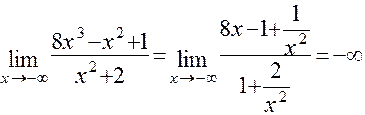 .
.
Задача 2. Задана функция 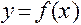 аналитическими выражениями для различных областей изменения независимой переменной:
аналитическими выражениями для различных областей изменения независимой переменной:
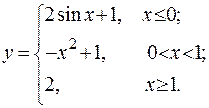
Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение. Из непрерывности элементарных функций на их естественной области определения следует, что точками разрыва нашей функции могут быть только точки 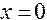 и
и 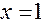 . Исследуем функцию на непрерывность в указанных точках, для чего найдем пределы функции справа и слева в этих точках. Если предел справа будет равен пределу слева и совпадет со значением функции в точке, то функция в точке непрерывна:
. Исследуем функцию на непрерывность в указанных точках, для чего найдем пределы функции справа и слева в этих точках. Если предел справа будет равен пределу слева и совпадет со значением функции в точке, то функция в точке непрерывна:
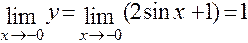 ;
; 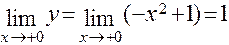 ;
; 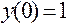 .
.
Из этих равенств следует непрерывность функции в точке 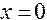 . Проверим, будет ли функция непрерывна в т.
. Проверим, будет ли функция непрерывна в т. 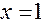 :
:
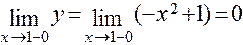 ;
; 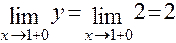 .
.
Так как 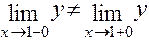 , то в точке
, то в точке 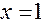 функция терпит разрыв первого рода (пределы справа и слева существуют и конечны).
функция терпит разрыв первого рода (пределы справа и слева существуют и конечны).
Для того чтобы сделать чертеж, изобразим графики функций 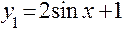 для
для 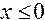 ;
; 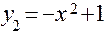 для
для 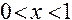 и
и 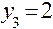 для
для 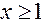 (рис. 3).
(рис. 3).
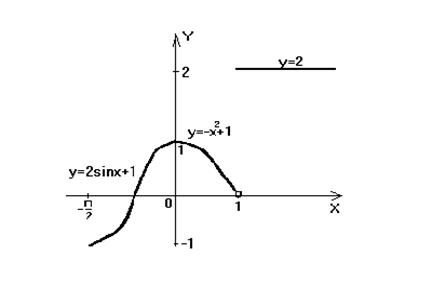
Рис.3
