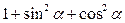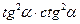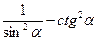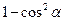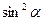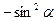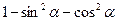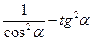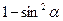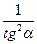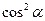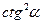ІІІ. Узагальнення та систематизація знань. 1. Дописати співвідношення між тригонометричними функціями одного аргументу
1. Дописати співвідношення між тригонометричними функціями одного аргументу
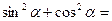
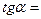
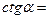
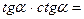
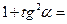
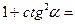
2. Самостійна робота (з подальшою перевіркою).
1) Установіть відповідність між поданими виразами та виразами, що їм тотожно дорівнюють (A – D)
| Варіант 1 | Варіант 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Відповідь:
|
Відповідь:
|
3. Знайдіть значення виразу: (можна користуватись довідковим матеріалом)
1) 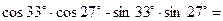 4)
4) 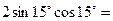
2) 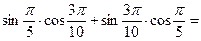 5)
5) 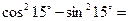
3) 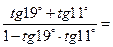 6)
6) 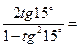
4. Кожен ряд отримує завдання, представник групи виконує на дошці, потім група перевіряє.
Знайдіть значення виразу:
І ряд II ряд III ряд
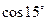 =
= 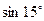 =
= 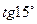 =
=
5. За допомогою формул перетворення суми тригонометричних функції в добуток (см. довідковий матеріал):
а) 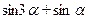
б) 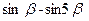
в) cos2x + cos3x
г) cosy – cos3y
6. Учні працюють в парах. Спочатку кожен виконує свій варіант, потім обмінюються роботами і перевіряють за допомогою довідкового матеріалу.
Установіть відповідність між тригонометричними рівняннями (1-4) та їхніми розв’язками. (А-D)
| Варіант 1 | Варіант 2 |
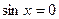 | А | 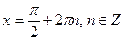 | |
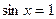 | Б | 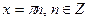 | |
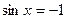 | В | 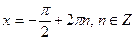 | |
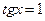 | Г | 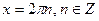 | |
| Д | 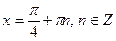 |
Відповідь:
| А | Б | В | Г | Д | |
| Х | |||||
| Х | |||||
| Х | |||||
| Х |
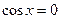 | А | 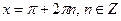 | |
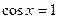 | Б | 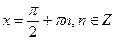 | |
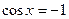 | В | 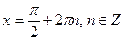 | |
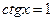 | Г | 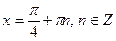 | |
| Д | 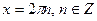 |
Відповідь:
| А | Б | В | Г | Д | |
| Х | |||||
| Х | |||||
| Х | |||||
| Х |
7. Розв'язати найпростіші тригонометричні рівняння:
1) 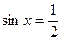 | 4) 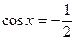 |
2) 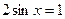 | 5) 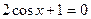 |
3) 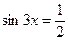 | 6) 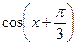 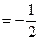 |
8. Дані рівняння розподілити по способах розв’язування тригонометричних рівнянь:
1. 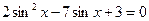
2. 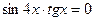
3. 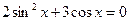
4. 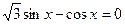
5. 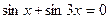
6. 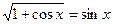
7. 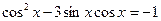
8. 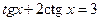
9. 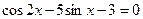
10. 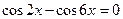
11. 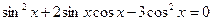
12. 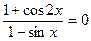
13. 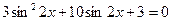
| Методи розв’язування рівнянь | Номер рівняння |
| Заміна змінних при розв’язуванні тригонометричних рівнянь | |
| Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом) | |
| Розв’язування однорідних тригонометричних рівнянь | |
| Зведення тригонометричного рівняння до однорідного | |
| Розв’язування тригонометричних рівнянь виду f(x) = 0 за допомогою розкладання на множники | |
| Відбір коренів тригонометричних рівнянь |
9. Розв'язати декілька рівнянь:
№1 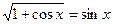
Розв'язання:
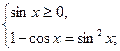
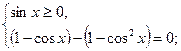
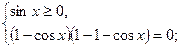
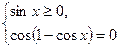
Тоді 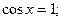
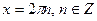 ; або
; або 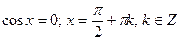 .
.
Враховуючи, що 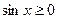 , маємо
, маємо 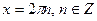 и
и 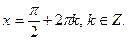
Відповідь: 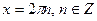 ;
; 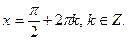
№2 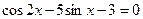
Розв'язання:
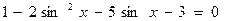 ,
,
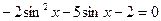 ,
,
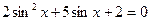 ,
,
нехай 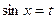 ,
, 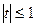 ,
,
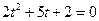 ,
,
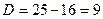 ,
,
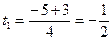 , , | 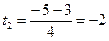 ; ; |
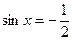 , , 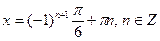 . . | 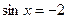 коренів немає, коренів немає, |
Відповідь: 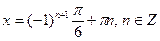 .
.
8. Показати розв’язання тригонометричної нерівності на одиничному колі:
1) 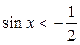 ; 2)
; 2) 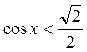 ; 3)
; 3) 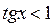 .
.
ІІІ. Підсумки уроку
ІV. Домашнє завдання
Довідковий матеріал
І. Тригонометричні тотожності
| . Формули суми | 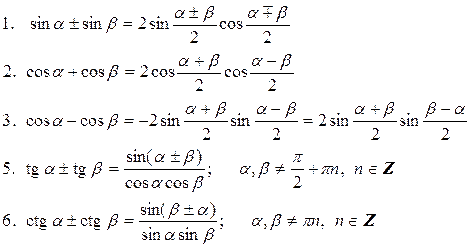 |
| Формули переведення добутку в суму або різницю | 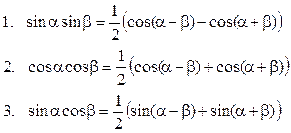 |
| Основна тригонометрична тотожність та наслідки з неї | 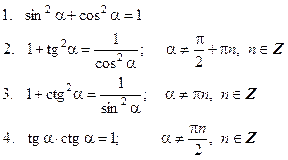 |
| Формули (теореми) додавання аргументів | 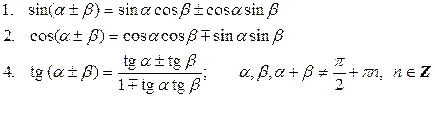 |
| Формули подвійного аргументу | 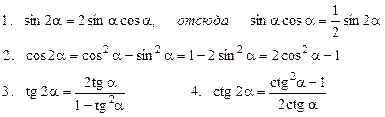 |
| Формули зниження степеня | 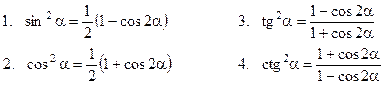 |
ІІ. Тригонометричні рівняння та нерівності
1.Найпростіші тригонометричні рівняння
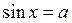 | 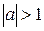 | коренів немає |
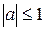 | 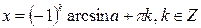 | |
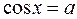 | 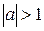 | коренів немає |
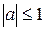 | 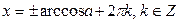 | |
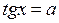 | 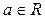 | 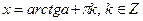 |
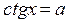 | 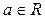 | 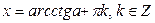 |
Окремі випадки
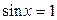 , , 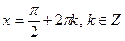 | 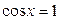 , , 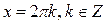 |
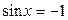 , , 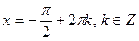 | 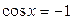 , , 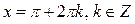 |
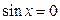 , , 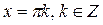 | 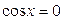 , , 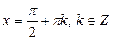 |
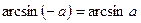 | 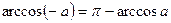 |
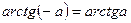 | 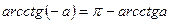 |
2.Приклади розв’язання найпростіших тригонометричних нерівностей
(за допомогою одиничного кола)
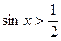 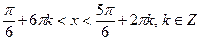 | 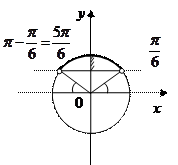 |
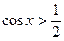 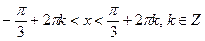 | 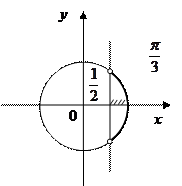 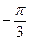 |
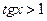 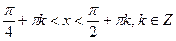 |   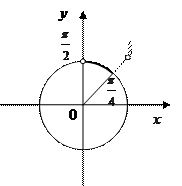 |
Дидактичний матеріал
№1. Найдіть значення виразу:
1) 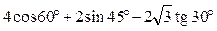 ; 3)
; 3) 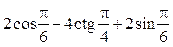 ;
;
2) 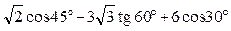 ; 4)
; 4) 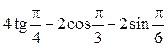 .
.
№2. Знайдіть значення тригонометричних функцій куту a, якщо відомо, що:
1) 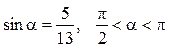 ; 2)
; 2) 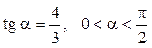 .
.
№3. Спростіть вираз:
1) 4cos23a + 4sin23a;
2) 1 – sin23x;
3) tg 3b ctg 3b;
4) tg a cos a;
5) (1 – cos 3b)(1 + cos 3b).
6) 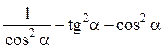 ;
;
7) cos4x – sin4x + sin2x.
№4. Доведіть тотожність:
1) 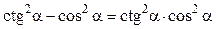 ;
;
2) 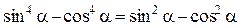 .
.
№5. Обчисліть:
1) sin 17° cos 13° + cos 17° sin 13°;
2) sin 20° cos 50° – cos 20° sin 50°.
№6. Спростіть вираз:
1) 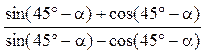 ;
;
2) 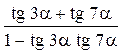 .
.
3) 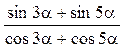 ;
;
4) 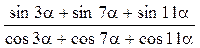 ;
;
5) 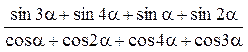 .
.
№7. Обчисліть:а) sin 15°; б) cos 75°.
№8. Дано: 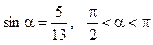 . Знайти sin 2a, cos 2a, tg 2a.
. Знайти sin 2a, cos 2a, tg 2a.
№9. Розв’язати рівняння:
1) 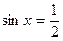 ; 4)
; 4) 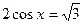 ; 7)
; 7) 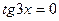 ;
;
2) 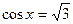 ; 5)
; 5) 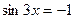 ; 8)
; 8) 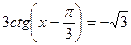 .
.
3) 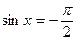 ; 6)
; 6) 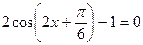 ;
;
№10 Розв’язати рівняння:
1) 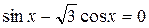 ;
;
2) 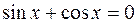 ;
;
3) 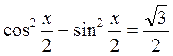 ;
;
4) 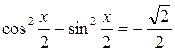
5) 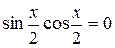 ;
;
6) 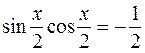 ;
;
7) 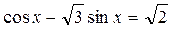 ;
;
8) 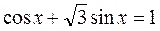 ;
;
9) 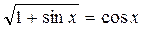 ;
;
10) 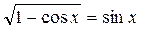 .
.
11) 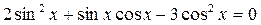
№11 Розв’язати рівняння:
1) 5cos2x+7cosx-6 = 0 ; 7) 7sin2x-2sinx = 0;
2) 5sin2x-7cosx+1 = 0; 8) sin2x+10cos2x = 0;
3) 8tg2x+10tgx+3 = 0; 9) 5cos2x-14cos2x+8 = 0;
4) cosx-2sinx = 0; 10) 3cos2x-14cosx+7 = 0;
5) cos2x+4cosx = 0; 11) 11sin2x+6cos2x+6 = 0;
6) sin3x-sin7x = 0; 12) 16cosx-11sinx-4 = 0.