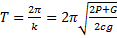Малые свободные колебания системы

Лекция 10. Исследование колебаний механических систем.

В данной лекции рассматриваются следующие вопросы:

1. Основные определения колебательного движения.

2. Малые свободные колебания системы.

3. Свободные колебания системы с учетом сил сопротивления движению.

4. Вынужденные колебания системы.

5. Влияние сопротивления на вынужденные колебания.

Изучение данных вопросов необходимо для изучения колебательных движений механической системы в дисциплине «Детали машин», для решения задач в дисциплинах «Теория машин и механизмов» и «Сопротивление материалов».

Основные определения колебательного движения.

Колебательным движением материальной системы называется такое ее движение, при котором она через некоторые промежутки времени постоянно возвращается к определенному положению.

Нетрудно обнаружить, что большинство окружающих нас систем совершают колебательное движение.

Если время, за которое все точки системы возвращаются к любому определенному положению с равными скоростями, постоянно и одинаково, то такое время Т называется периодом колебаний. А эти колебания – периодическим колебательным движением.

На рис.1 показан пример изменения какой-то обобщенной координаты q при довольно сложном колебательном процессе. А на рис.2 – при более организованных, периодических колебаниях.

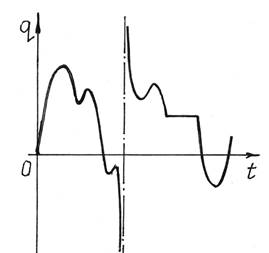
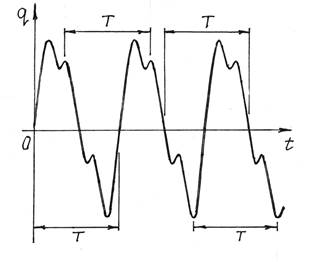
Рис.1 Рис.2

При периодическом процессе значения функции, описывающей движение системы, повторяются через каждый период Т, т.е.

q(t)=q(t+T). (1)

Если эта функция имеет вид

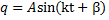, (2)

то такое колебательное движение называется гармоническим. График такого движения дан на рис.3.

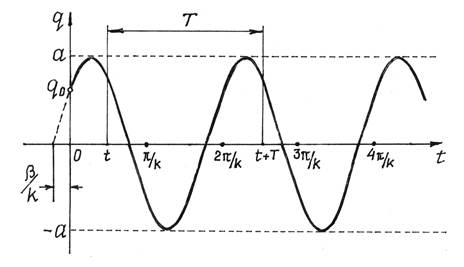
Рис.3

По (2) 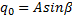– начальная координата, определяющая положение системы в начале движения;

A – амплитуда колебаний, имеет размерность обобщенной координаты;

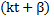– фаза колебаний, 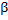– начальная фаза;

k – частота колебаний, размерность ее с^-1.

Период колебаний найдем используя свойство (1):

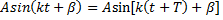
Отсюда, т.к. период синуса равен 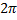, 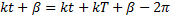. Значит, период колебаний

Вообще, существует много всяких типов колебаний. Выделим, в первую очередь, линейные и нелинейные колебания. Названия их определяются видом дифференциальных уравнений, которые описывают колебательное движение материальной системы.

Исследование нелинейных колебаний значительно усложняется, т.к. нет общих методов решения нелинейных дифференциальных уравнений.

Но, если рассматривать малые колебания, такие, при которых координата и скорость изменяются на малую величину, то многие нелинейные уравнения станут линейными и исследование движения значительно упростится.

В дальнейшем мы будем рассматривать лишь малые, линейные колебания. И, мало того, колебания системы только с одной степенью свободы.

Естественно, колебания системы могут совершаться только около устойчивого положения равновесия.

Если система консервативная, то найти положение равновесия и определить устойчивость его можно с помощью потенциальной энергии.

Ранее было установлено, что в положении равновесия выполняется условие 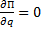и если в положении равновесия 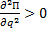, то равновесие будет устойчиво.

Договоримся отсчитывать координату от положения равновесия 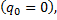а потенциальную энергию там считать равной нулю (П₀=0) Тогда, по определению малых колебаний, обобщенная координата q всегда будет малой величиной.

Разложим потенциальную энергию в ряд Маклорена около положения равновесия:

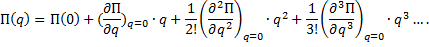
Так как П(0) = 0 и 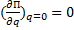и, отбросив члены третьего и выше порядка малости, получим

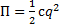, (4)

где коэффициент 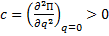по условию устойчивости.

Поэтому потенциальная энергия колебательной системы, отсчитываемая от положения устойчивого равновесия, будет всегда положительной.

Кинетическую энергию системы при малых колебаниях также можно преобразовать.

Кинетическая энергия системы 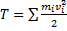, а так как радиус-вектор точек 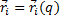и q=q(t), то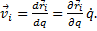

Поэтому 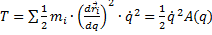, где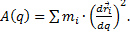

Эту функцию A(q) можно разложить в ряд Маклорена по степеням q около положения равновесия и учесть только первый член: A(q)=A(0)+… . Остальные члены можно не учитывать, т.к. после подстановки A(q) в Т, они станут величинами третьего и выше порядка.

Обозначив постоянную A(0)=a получим

T=aq²/2. (5)

Коэффициент a называется коэффициентом инерции. Конечно, a>0 т.к. кинетическая энергия не может быть отрицательной.

Замечание. Практически, при исследовании конкретных колебательных систем приходится раскладывать в ряд функции, содержащие, чаще всего, sinx, cosx, e^x. Разложение их с точностью до малых второго порядка известны: sinx=x, cos=1-x²/2, e^x=1+x+x²/2.

Малые свободные колебания системы.

Свободными колебаниями называется колебательное движение системы, выведенной из положения равновесия и предоставленной самой себе.

Составим уравнение Лагранжа для консервативной системы:

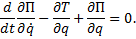
Используя (4) и (5), получим дифференциальное уравнение свободных колебаний 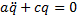или, обозначив c/a=k²,

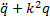=0. (6)

Решение этого однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами известно:

q=C₁coskt+C₂sinkt (7)

или, использовав другие постоянные 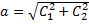и ,

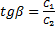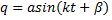. (8)

Следовательно, малые свободные колебания – гармонические колебания, причем амплитуда колебаний и начальная фаза определяются начальными условиями (q и 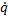при t = 0), а частота колебаний k и период Т не зависят от начальных условий, определяются только конструкцией системы.

Обычно частоту колебаний находят сравнением полученного дифференциального уравнения с уравнением (6).

Пример 1. Тело весом Р подвешено на нити, перекинутой через блок и прикрепленной к пружине (рис.4). Вес блока G, радиус - r; жесткость пружины с. Определим период свободных колебаний системы.

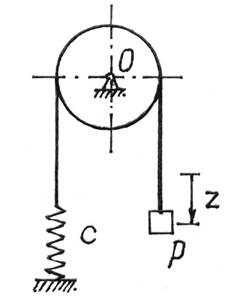
Рис.4

Назначим обобщенной координатой смещение z груза по вертикали от положения равновесия, при котором пружина была растянута на величину f.

Тогда потенциальная энергия относительно положения равновесия 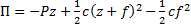. Где (z+f) - полная деформация пружины, а cf²/2 - потенциальная энергия пружины в положении равновесия, которую вычитаем из потенциальной энергии полностью деформированной пружины. Раскрыв скобки, получим

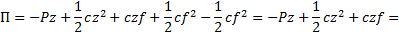
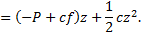
В положении равновесия должно выполняться условие 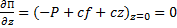. Отсюда P=cf, значит, П=cz²/2

Кинетическая энергия системы

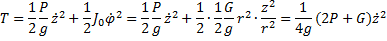
Составив уравнение Лагранжа, получим 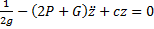или 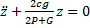Сравнивая с (6), находим частоту колебаний 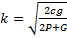и затем период