Определение момента инерции твердого тела
Методом колебаний
Контрольные вопросы
1.Запишите уравнение собственных незатухающих колебаний. Дайте определения основных характеристик колебательного движения: амплитуды; фазы; периода; частоты; циклической частоты.
2.Запишите зависимость скорости колебательного движения от времени. Чему равно максимальное значение скорости?
3.Что называют моментом инерции тела относительно данной оси? Как рассчитать момент инерции материальной точки, твердого тела? В каких единицах измеряется момент инерции?
4.Сформулируйте теорему Штейнера. Сделайте поясняющий рисунок.
5.Запишите формулы для момента инерции шара и кубика относительно любой оси, параллельной оси, проходящей через центр масс этих тел.
6.Запишите формулу кинетической энергии тела, вращающегося относительно некоторой оси.
Тесты
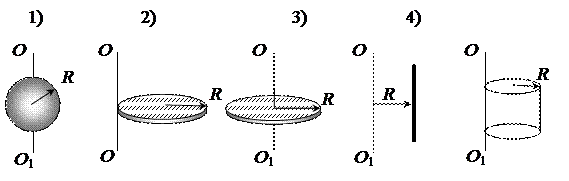
1.Шар (1), два диска (2 и 3), тонкий стержень (4) и тонкостенный цилиндр (5) имеют одинаковую массу m. Какое из этих тел имеет момент инерции относительно оси ОО1, равный I = mR2?
Варианты ответа: а) 1; б) 2; в) 3; г) 4; д) 5; е) 1 – 3; ж) 1 – 4;
 |
з) все тела имеют момент инерции I = mR2 ; и) среди ответов а - з нет верного.
2.Проволока AOB, согнутая под углом a (рис. 2.20), расположена в плоскости xOy. Как изменятся моменты инерции проволоки относительно осей Ox, Oy, Oz, если угол a увеличить?
| Варианты ответа | Относительно оси Ox | Относительно оси Oy | Относительно оси Oz |
| уменьшится | уменьшится | уменьшится | |
| увеличится | уменьшится | не изменится | |
| увеличится | увеличится | не изменится |

3.Сравнить моменты инерции однородного диска с вырезом (рис. 2.21) относительно осей Ox и Oy.
Варианты ответа: 1) IOx = IOy; 2) IOx > IOy; 3) IOx < IOy.
4.Сравнить моменты инерции однородной пластины относительно осей I и II (рис. 2.22). Пластина и обе оси расположены в плоскости рисунка, при этом ось I проходит через центр масс пластины.
Варианты ответа: 1) II = III; 2) II < III; 3) II > III.
5.Какова полная кинетическая энергия цилиндра массой m при качении без скольжения со скоростью v по плоской поверхности?
Варианты ответа: 1) 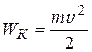 ; 2)
; 2) 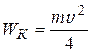 ; 3)
; 3) 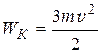 ;
;
4) 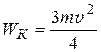 ; 5)
; 5) 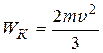 .
.
6. 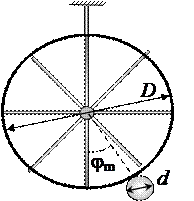 Колебания махового колеса заданы уравнением j = 0,5 cos (2t + p/3) рад. Чему равны амплитуда и период колебаний колеса?
Колебания махового колеса заданы уравнением j = 0,5 cos (2t + p/3) рад. Чему равны амплитуда и период колебаний колеса?
Варианты ответа:
1) jm = 3рад, Т = 2 с; 2) jm = 0,5 рад, Т = 2 с;
3) jm = 0,5 рад, Т = p; 4) jm = 2 рад, Т = p/2;
5) jm = 0,5 рад, Т = p/3; 6) jm = 1 рад, Т = p;
7) jm = 1 рад, Т = -p; 8) jm = 1 рад, Т = p/3.
7.Маховое колесо совершает колебания. Какие из перечисленных величин достигают максимального значения в крайнем положении груза: угловая скорость w, угловое ускорение e, кинетическая энергия T, потенциальная энергия П ?
Варианты ответа: 1) w, П; 2) w, Т; 3) e, П; 4) w, e, П.
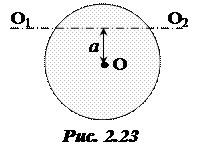
8.Определить момент инерции однородного шара относительно неподвижной оси вращения О1О2, положение которой показано на рис. 2.23. Масса шара m, его радиус R.
Варианты ответа:
 1)
1) 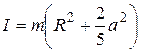 ;
;
2) 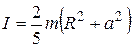 ;
;
3) 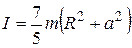 ;
;
4) 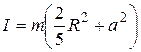 .
.
9.На тело, вращающееся вокруг неподвижной оси, действует постоянный вращающий момент. Какая из перечисленных ниже величин изменяется со временем по линейному закону:
1) момент инерции тела;
2) угловое ускорение;
3) кинетическая энергия тела;
4) момент импульса тела относительно оси вращения;
5) угловая скорость;
6) ни одна из перечисленных величин не меняется по линейному закону.
10. 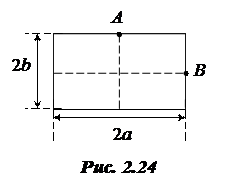 Однородная пластинка со сторонами 2а и 2b массы m (рис. 2.24 )имеет момент инерции IB относительно оси Z, проходящей через точку В перпендикулярно плоскости пластинки. Найти момент инерции пластинки IA относительно оси, проходящей через точку А и параллельной оси Z.
Однородная пластинка со сторонами 2а и 2b массы m (рис. 2.24 )имеет момент инерции IB относительно оси Z, проходящей через точку В перпендикулярно плоскости пластинки. Найти момент инерции пластинки IA относительно оси, проходящей через точку А и параллельной оси Z.
Варианты ответа: 1) IB + m(a2 + b2);
2) IB + m(a2 - b2); 3) IB + m(b2 – a2);
5) нет верного ответа.
11.Определить момент инерции однородного диска радиусом R и массой m относительно оси, перпендикулярной плоскости диска и проходящей через середину одного из радиусов.
Варианты ответа: 1) 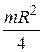 ; 2)
; 2) 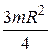 ; 3) mR2; 4)
; 3) mR2; 4) 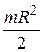 .
.
Лабораторная работа 3-1
