Определение скорости звука в воздухе

Цель работы: определить длину волны и скорость звука в воздухе методом фигур Лиссажу, определить показатель адиабаты.

Оборудование: звуковой генератор ADG-1005, трубка с телефоном и микрофоном, осциллограф ADS-2111M.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Звук – это волны в упругих средах. В газах звуковые волны − это процесс распространения областей сжатия – разрежения.

Уравнение волны – это зависимости параметра ψ (давления, смещения и т.д.)в некоторой точке пространства от времени и от расстоянии Z до источника. Если колебания источника происходят по уравнению 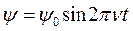, то частицы среды начинают колебания позже, чем источник, на время распространения волны 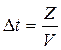. Тогда уравнение волны имеет вид

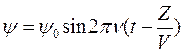. (1)

Получим формулу скорости распространения звуковой волны в газе. Пусть мембрана телефона, находящаяся у основания воображаемой трубки с площадью сечения S, начала движение с дозвуковой скоростью U. Частицы газа, прилегающие к мембране, приходят в движение с такой же скоростью. Воздух перед мембраной сжимается и сжимает последующие слои газа. Граница между сжатым и невозмущенным газом является фронтом волны. Она перемещается со скоростью звука V (рис. 1).

Применим для определения скорости звука уравнение второго закона Ньютона для движущейся массы газа: изменение импульса газа равно импульсу силы со стороны мембраны: dm U = F dt . Массу газа определим как произведение плотности на объем: dm =r dL∙S, а силу давления мембраны на газ как повышение давления на площадь: F = dp∙S. Примем, что отношение скоростей мембраны и фронта пропорционально отношению проходимых ими расстояний: 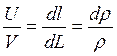, которое, в свою очередь, равно относительному изменению плотности газа. Подставив полученные преобразования в уравнение второго закона Ньютона, произведя замену dL=Vdt, получим уравнение 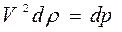. Откуда .

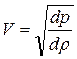Вследствие кратковременности процессы сжатия–разрежения газа в звуковой волне являются адиабатическими, без теплообмена между нагретой областью сжатия и охлажденной областью разрежения. Поэтому применим уравнение Пуассона 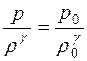. Дифференцируя 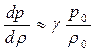и подставляя, получим формулу скорости звука

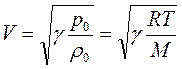. (2)

В формуле произведена замена давления по уравнению Менделеева–Клапейрона 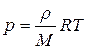. Здесь R = 8,31 Дж/моль∙К – газовая постоянная, Т – абсолютная температура, М = 28,9 10 ^–3 кг/моль – масса моля воздуха, g – показатель адиабаты (теоретически для двухатомных газов γ = 1,4).

В лабораторной установке звук распространяется в трубке от телефона к микрофону (рис. 2). Электрические колебания от телефона и микрофона подаются соответственно на горизонтальный и вертикальный входы осциллографа. На экране наблюдается результат сложения электрических колебаний одинаковой частоты в виде так называемых фигур Лиссажу. Фигура Лиссажу − это повторяющаяся траектория движения точки, участвующей в двух взаимно перпендикулярных колебаниях, если соотношение частот равно отношению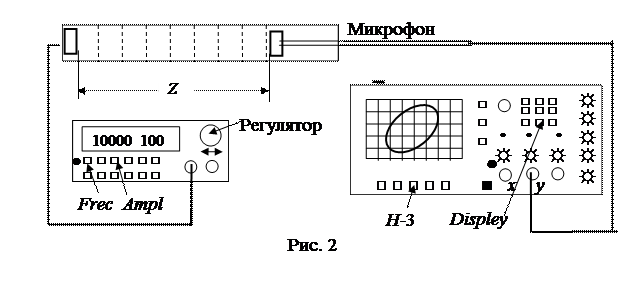
целых чисел.

Теоретически рассмотрим сложение взаимно перпендикулярных колебаний одинаковой частоты. Пусть разность фаз кратна целому числу 2p радиан: x = A ₁cos 2pn t, y = A ₂cos 2pn t . Для получения уравнения траектории y(x) исключим время t, поделив уравнения. В результате получим 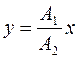. Это уравнение прямой линии, проходящей через 1−3 квадранты в прямоугольник размером 2А₂– 2А₁.

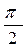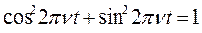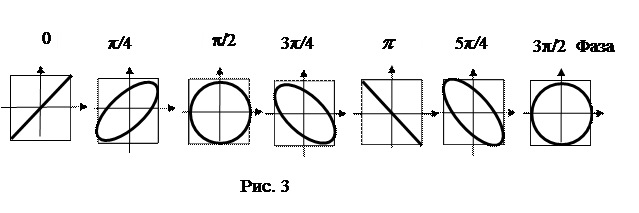
Пусть разность фаз кратна нечетному числурадиан, так что х= A ₁cos2pn t, y=A ₂sin2pn t. Исключим время t по соотношению . В результате получим для фигуры Лиссажу уравнение эллипса: 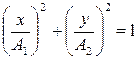, вписанного в прямоугольник 2А₂– 2А₁. Вид фигуры Лиссажу зависит от разности фаз (рис. 3).

Согласно уравнению волны (1) разность фаз колебаний мембран микрофона на расстоянии Z от источника звука и телефона в начале координат равна 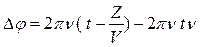. Откуда

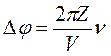. (3)

При перемещении микрофона в трубке превращение на экране осциллографа эллипса опять в эллипс или прямойв такую же прямую линию происходит, если разность фаз возрастает на целое число 2p радиан, то есть 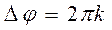, где k = 0,1,2,3 – целое число. Подставив в уравнение (3) условие повторения фигуры Лиссажу, получим формулу связи расстояния между телефоном и микрофоном с числом длин волн между ними

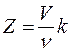. (4)

ВЫПОЛНЕНИЕ РАБОТЫ

1. Включить в сеть 220 В генератор. Нажать кнопку Freq, еслиона не светится и регулятором установить частоту генератора около 400 Гц. Нажать кнопку Ampl и установить напряжение около 10 В.

2. Включить в сеть 220 В осциллограф. На экране появится фигура Лиссажу, если сохранились настройки с предыдущего занятия. Если нет, то нажмите кнопку Displey. На дисплее появится окно диалога. Нажмите кнопку H-3 включения XY режима сложения взаимно перпендикулярных колебаний. Ручками усиления каналов CH-1 и CH-2 сформируйте изображение фигуры.

3. Пододвиньте микрофон на минимальное расстояние к телефону, получив при этом некоторое изображение фигуры Лиссажу. Запишите координату микрофона в таблицу при к = 0. Отодвигайте микрофон до конца трубки, отмечая каждый раз координату микрофона при повторении выбранного изображения фигуры Лиссажу. Результаты запишите в таблицу. Таблица

k
Z, см

Выключить приборы.

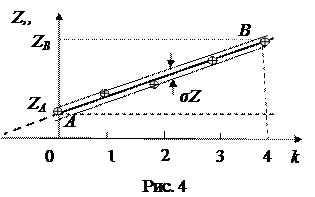
4. Построить график зависимости координаты микрофона Z от числа длин волн к между микрофоном и телефоном. Размер графика не менее половины страницы. Около точек провести прямую линию (рис. 4).

5. Определить среднее значение скорости звука по угловому коэффициенту. Для этого на экспериментальной линии как на гипотенузе построить прямоугольный треугольник (рис. 4). По координатам вершин треугольника

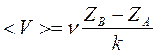. (5)

6. Оценить случайную погрешность измерения скорости .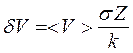

Записать результат в виде V=<V>±δV, P=0,9.

7. Определить по формуле (2) среднее значение показателя адиабаты. Сравнить с теоретическим значением для двухатомного газа γ = 1,4. Сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Объясните процесс распространения звука в газах. Дайте понятие фронта волны.

2. Запишите формулу для скорости звуковых волн в газах. Объясните, почему процесс сжатия – разрежения газа в звуковой волне адиабатический.

3. Запишите уравнение плоской волны. Дайте понятие фазы.

4. Дайте определение фигуры Лиссажу. Выведите уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты, при разности фаз 2πk радиан.

5. Выведите уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты, при разности фаз p/2 рад.

6. При каком наименьшем изменении расстояния между микрофоном и телефоном фигура Лиссажу принимает первоначальный вид.

Термодинамика

Работа 15