Озгалмайтын өске қатысты қатты -дененің айналмалы қозгалысы

Атты дененің ілгерілемелі қозғалысы.

Анықтама.Қозғалушы денемен өзгерместей бекітілген кез келген кесінді өзіне – өзі параллель қала берсе қатты дене қозғалысын ілгерілемелі қозғалысдеп аталады.

Ілгерілемеліқозғалыстағықатты дененіңбарлық нүктелерініңкез келген уақыт кезеңіндегі кинематикалық сипаттамалары (траекториялары, жылдамдықтары және үдеулері) бірдей. Ілгерілемелі қозғалыстағыдененүктелерінің траекториялары әр түрлі болуы мүмкін: түзу сызықты және қисық сызықты.

Берілген қатты дененің ілгерілемелі қозғалысты зерттеу үшін Oxyz қозғалмайтынкоординаттар жүйесінтаңдап алалық(7.1 – сурет).

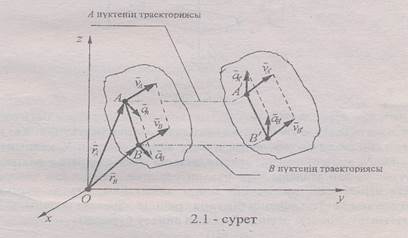7.1 - сурет

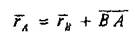Ілгерілемелі қозғалыстағы қатты дененің кез келген А және В нүктелері үшін мына векторлык теңдеуді жазуға болады:

(7.1)

Мұнда ~ВА - модулі және бағыты түрақты веқтор. (7.1) теңдеудің екі жағынан уақыт бойынша туындыны алғанда, мынаған келеміз:

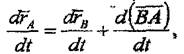Ян ~Л

Бұл теңдеуде

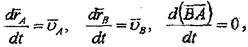Бұл теңдіктің екі жағынан туындыны алсак, онда алатынымыз:

а_А=а_в.

Сонымен, тек ілгерілемелі қозғалыс кезінде ғана түтас дененін жылдамдығы мен үдеуі туралы сөз қозғалуға болады.

озгалмайтын өске қатысты қатты -дененің айналмалы қозгалысы

Анықтама.Егер қозғалыстағы дененің кемінде екі нүктесі тыныштық қалпын сақтайтын болса, онда осы дене қозғалмайтын еске қатысты айналмалы қозгалыс жасайды. Осы екі нүкте арқылы жүргізілген түзуді дененің айналу өсі деп атайды.

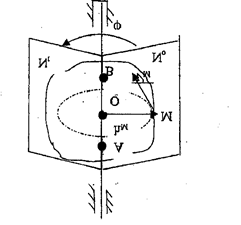7.2 – сурет

Айналу өсі арқылы өтетін N жазықтығын денемен бірге бекітейік (7.2 -сурет). Бастапқы кезеңде (t1=0) ол жазықтыкты Nо деп белгілейік. Кез келген t уақыт өткен соң ол жазықтык денемен бірге айнала отырып N, қалпына келеді. Осы N және N, жазықтарының арасындағы екі жақты бүрыш <р капы дсненін айналу бүрышы деп аталады. Бүл бұрыш берілген дененің кез келген уақыт кезеңіндегі кеңістіктегі орньш бір мәнді анықтайды, демек, тұрақты өсті айнала қозғалатын қатты дененің бір ғана еркіндік дәрежесі болады.

Уақыттың функңиясы ретінде берілген айналу бүрышы

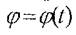. (7.1.)

Қатты дененің айналу заңы немесе айналу теңдеуі деп аталады. Бұл айналу тұтас қатты дененің негізгі кинематикалық сипаттамасы болып табылады.

Дененің бүрыштық жылдамдығы

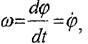(7.2)

бүрыштық удеуі

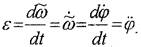(7.3)

Бұл шамалар тұтас қатты денеге тең.

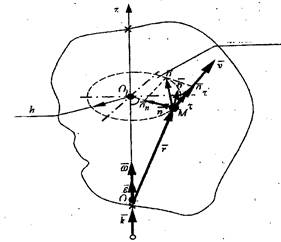Айналу ксзінде қатты дененің барлық нүктелерінің жылдамдықтары айналу өсіне перпендикуляр, және центрлері айналу өсінде жататын шеңберлерді сызады (7.3 - сурет).

М нүктесінің

траекториясы

7.3 -сурет.

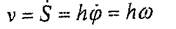Кез келген М нүктесінің айналмалы қозғалыстағы қатты дененің алгебралык жылдамдығы мынадай болады:

яғни дененің бұрыштық жылдамдығы мен нүктенің айналу өсінен қашықтығының көбейтіндісіне тең. Өйткені берілген М. нүктесі үшін оның айналу радиусы деп аталатын бүл қашықтық Һ = |О,М| = сопst, яғни дене абсолют қатты дене. Сонымен, кез келген уакыт кезіндегі дене нүктелерінің жылдамдыктары олардың айналу радиустарына тура пропорционал. М нүктесінің жылдамдығының бағыты жанаманымен дененің айналу бағытына қарай бағытталады.

Жоғарыда М нүктесі жылдамдығының шамасы және бағыты туралы

айтылғандарды ескерсек,

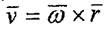(7.5)

екенін кору қиын емес. Бүл формула Эйлер формуласы деп аталады.

Дене нүктелерінің үдеулерін табу .үшін (2.5) өрнегінен уақыт бойынша туындыны алайық, онда М нүктесінің үдеуі

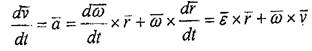
(7.6)

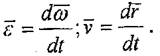болады, мұнда

Соңғы теңдіктің оң жағындағы қосылғыштардың біріншісі - жанама үдеу, екіншісі - нормаль үдеу, қорытындысында былай жазамыз:

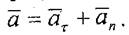
(7.7)

Олардың шамалары

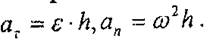
(7.8)

Нүктенің толық үдеудің модулі

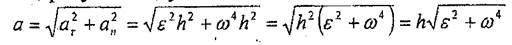
(7.9)

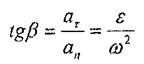Үдеу вектордың бағыты оның Һ = ОМ векторымен жасайтын бүрышымен анықталады:

(7.10)

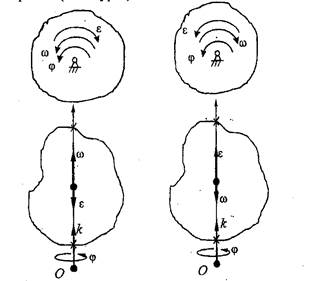
Енді бүрыштык жылдамдық пен бүрыштық үдеуді веқторлар ретінде қарастырайық (7.4 - сурет).

7.4 - сурет

Бұрыштық жылдамдықтын болуы айналу өсімен тығыс байланысты болғандықтан оны айналу есінің бойында жаткан вектор деп қарауға болады. Онын бағытын және айналу өсіндегі орнын таңдау біздіп еркімізде, сондыктан да ол сырғымалы вектор болғаны.

Бұрыштык. жылдамдық уақыт өтуімен байланысты тек шамасын ғана өзгертетін болғандыктаы бүрыштық үдеу векторы ё да айналу өсінің бойында орналасады. Оны аналитикалық жолмен де дәлелдеуге болады. Бұрыштық жылдамдық векторын былай жазайық:

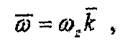
(7.11)

мұнда "к - айналудың оң бағытын көрсететін немесе Оz. айналу өсінің бірлік векторы. СИ жүйесіндегі бүрыштық жылдамдыктың өлшемі -рад/с.

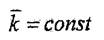Айналу өсі қозғалмайтын болғандықтан оның бірлік векторы түрақты, яғни

Сондыктан (7.11) теңдігінің екі жағында уақыт бойынша туынды аламыз:

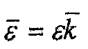
(7.12)

СИ жүйесіндегі бұрыштық үдеудің өлшемі - рад/с².

Егер ε > 0 , онда дененің айналуы •- удемелі, яғни а және е векторлары бағыттас болғаны, ал е < 0, айналу - кемімелі болады да, ω және ε векторлары бір-біріне қарама-қарсы бағытталады.

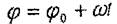Егер дененің бүрыштық жылдамдығы түрақты болса (ω=const), онда дененің айналуы — бірқалыпты айналу делінеді, ал айналу заңы болады.

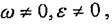Егер, онда

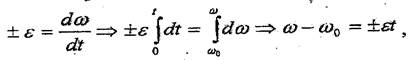
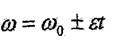
(7.13)

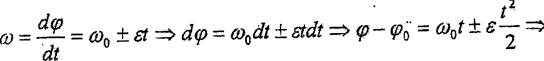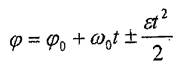(7.14)

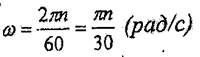Көп жағдайларда түрлі машиналардын минуттык айналу саны п беріледі. Одан бүрыштық жылдамдыққа көшу үшін

(7.15)

өрнегі пайдаланады, ал айналу бүрышы дененің айналу саны N арқылы былай

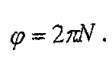анықталады

(7.16)

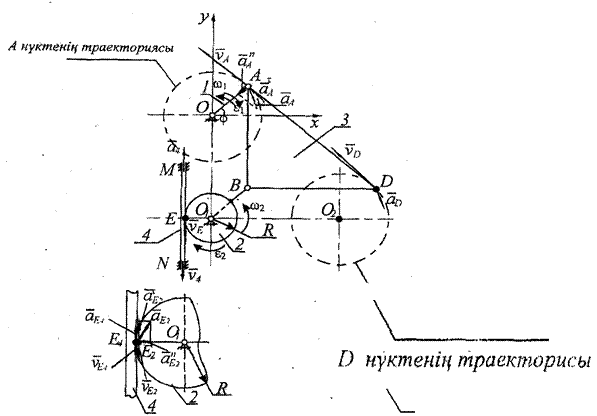
7.1 мысал.Көрсетілген (7.5 - сурет) механизмдегі 1-ші мен 2-ші денелер қозғалмайтын табанмен О және О₁ цилиндрлік шарнирлармен, ал 3-ші дене 1-ші мен 2-ші денелермен А және В цилиндрлік шарнирдармен байланыскан. 4-ші дене Е нүктесінде 2-ші денеге қатысты сырғанамай МN түзу бойымен қозғалады.

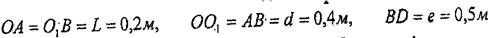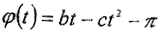АВ ВD. - суреттің жазықтығына перпендикуляр О нүктесінен өтетін Ог өсіне қатысты 1-ші сырықтың айналмалы қозғалысының заңы

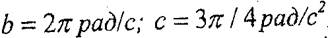түрде берілген. Мұнда

Уақыт г,=1с мезетіндегі 1-ші мен 2-ші денелердің бұрыштық жылдамдықтары мен бұрыштық үдеулерін анықтау керек, сонымен қатар

А, D , Е нүктелерінің және 4-ші дененің жылдамдықтары мен үдеулерін табу

керек. Табылған қозғалыстың кинематикалық сшіаттамалары мен А және D

нүқтелерінің траекторияларын - суретте көрсету керек.

Шешуі.Қарастырып отырған механизмдегі 1-ші және 2-ші денелер

айналмалы қозғалыс жасайды (олардың қозғалмайтын айналу өстері О және О₁

цилиндрлік шарнирлердің өстеріне дәл келеді).

Уакыт өткен сайын (әр мезетте) А және 5 нүктелер арқылы ететін түзу

вертикаль, ал В және D нүктелерден өтетін түзу горизонталь бағытын

сақтайды, сондықтан 3-ші дене ілгерілемелі қозғалыс жасайды. МN бағытта 4

дене де ілгерілемелі қозғалады.

2.5 - сурет

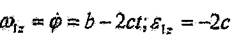Оz айналу өсіне 1-ші дененің бүрыштық жылдамдығы мен бұрыштық үдеуінің проекциялары

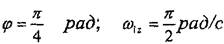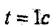формулалармен анықталады. мезетінде ;

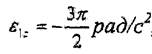
ал бұрыштық жылдамдык пен бұрыштық үдеудің модульдары

.

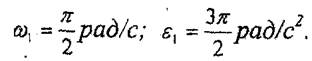1-ші дененің бұрыштық жылдамдығының бағыты

доғалық стрелкамен корсетілген, оның бағыты φбұрышын санаудын оң бағытымен

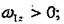
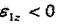бірдей, яғни ; ал болғандықтан, бұрыштық үдеудің доғалық стрелкасы қарама-қарсы багытталады (7.5,а - суретті кара).

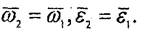Айналмалы қозғалыстағы 1-ші мен 2-ші денелердің айналу бүрыштары бірдей, сол себептен

.

Айналмалы козғалыстан 1-ші дененің А нүктесінің жылдамдығы,

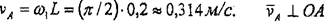және 1-ші дененің бүрыштық

.жылдамдығының доғалық стрелкасына сәйкес бағьгтталады, ал модулі

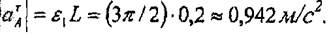Үдеудің нормаль құрушысы аⁿ_A А нүктеден О нүктеге қарай бағытталады.

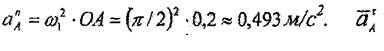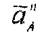және

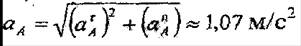векторлар арқылы қүрылған тік төртбұрыштың диагоналінде жататын А нүктесінің толық үдеуінің модулі

(7.5,а – суретті қара).

Ілгерілемелі қозғалыстағы 3-ші дененің барлық нүктелерінің жылдамдықтары мен үдеулері бірдей сол дененің жылдамдык пен үдеуіне тең болады, яғни

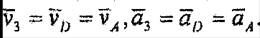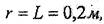А нүктесінің траекториясы радиусы

центрі О (0,0) нүктеде болатын шеңбер, ал I) нүктесінің траекториясы дәл сондай шеңбер, бірақ оныц О₂ центрінің координаттары

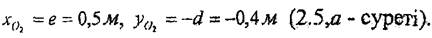Е нүктеде түйісетін 2-ші мен 4-ші денелерде Е_г мен Е_А нүктелерді белгілейік. Нүьсте Е_г 2-ші дененің нүктесі деп,

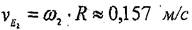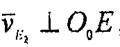деп аламыз;

ал бүл вектордың бағыты 2-ші дененің бүрыштық жылдамдығының доғалық стрелкасына сәйкес бағытталады;

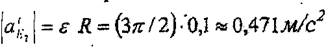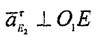мұнда және 2-ші дененін бүрыштык үдеудің бағытьша сәйкес,

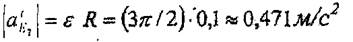Вектор а", Е нүктеден О, нүктеге қарай бағытталады, ал модулі

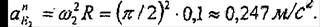Толық үдеудің модулі (7.5,б - суретгі қара)

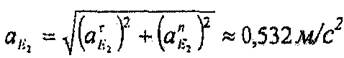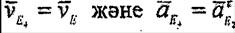Түйісу Е нүктеде 4-ші дене 2-ші денеге катысты сырғаиамай козғалатындықтан

,яғни Е₄ - нүктенің толық үдеуі Е₂ нүктенің үдеуінің жанама қүрушысына тең. Ілгерілемелі қозғалыстағы 4-ші дененің барлык нүктелерінің жылдамдықтары мен үдеулері Е₄ нүктенің жылдамдық пен үдеуіне тең:

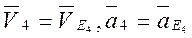(7.5 – суретті қара)

ГЛОССАРИЙ

Абсолют қатты дене	Абсолютно твердое тело	Rigid body
Қатты дененнің ілгерлемелі қозғалысы	Поступательное движение твердого тела	Translator motion of rigid body
Тұрақты өске қатысты қатты дененің айналмалы қозғалысы	Вращательное движение твердого тела вокруг неподвижной оси	Motion of rigid body about fixed axis
Дененің айналу бұрышы	Угол поворота тела	Angle of rotation
Бұрыштық жылдамдық	Угловая скорость	Angular velocity
Бұрыштық үдеу	Угловое ускорение	Angular acceleration

Тақырыпка қатысты сүрактар:

1. Қозғалыстағы катты дененің екі нүктесінін жылдамдықтары және
үдеулері бірдей. Бұл дененің козғалысы ілгерілемелі деп айтуға бола
ма?

2. Дене нүктелерінің траекторияяары - шеңберлер. Дене айналмалы
қозгалыс (немесе ілгерілемелі қозғалыс) жасайды деп айтуға бола ма?

3. Дене бірқалыпты айналады. Оның барлық нүктелер үшін V = сопst деп
түжырымдауга бола ма?

4. Айналып түрған дененің қандай нүктелерінің үдеулері: а) модульдары
бірдей; б) бағыттары бірдей; в) модульдары және бағыттары бірдей?

5. Қозғалмайтын өске қатысты айналып түрған дененін кез келген
нүктесінің жылдамдық жене үдеу векторлары өзара перпендикуляр
болуы мүмкін ба? Бір түзуімен бағытталған мүмкін ба?

6. Дененің айналуы үдемелі ме кемімелі ме ю-ның немесе е-нын
таңбасьшен ғана анықтауға бола ма?

7. Айналып түрған табақша нүктелерінің үдеулердің векторы оның
радиусымен β=45°жасайды. Осы табақшаның бүрыштык жылдамдык
пен бүрыштык үдеудің модулъдерінің ара қатынасы неге тен?