Коэффициент детерминации в регрессионной модели

Коэффициент детерминации (R²)— это доля дисперсии отклонений зависимой переменной от её среднего значения, объясняемая рассматриваемой моделью связи. Модель связи обычно задается как явная функция от объясняющих переменных.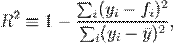

где y_i — наблюдаемое значение зависимой переменной, а f_i — значение зависимой переменной предсказанное по уравнению регрессии 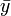-среднее арифметическое зависимой переменной. Коэффициент детерминации является случайной переменной. Он характеризует долю результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака: 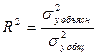0≤ R²≤1. причем если R²= 1 то переменная y_t полностью объясняется регрессором x_t. В множественной регрессионной модели добавление дополнительных регрессоров увеличивает значение коэффициента детерминации, поэтому его корректируют с учетом числа независимых переменных: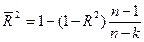

Ковариация, коэффициент корреляции и индекс детерминации.

Наряду с функцией регрессии в эконометрике существенно используются числовые характеристики взаимосвязи пары случайных переменных (x, y). Эти характеристики именуются ковариацией и коэффициентом корреляции. Ковариацией называется константа 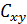, определенная по правилу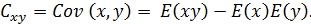

Свойства математического ожидания позволяют представить 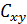и так: 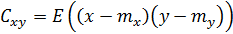, где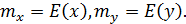

Оценкой ковариации служит величина 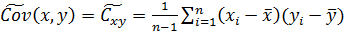, именуемая выборочной ковариацией.

Так же размерность 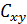равна произведению значений размерности случайных переменных x и y. Часто удобно использовать безразмерную ковариацию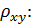

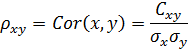
Константа 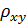именуется еще коэффициентом корреляции. Всегда .

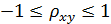В качестве меры, объясняющей способности регрессора в модели (1)

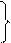
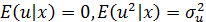
может служить в пределах обучающей выборки ( 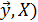величина .

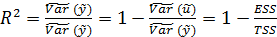Она именуется коэффициентом детерминации модели и равна доле эмпирической дисперсии переменной y, которая в рамках обучающей выборки ( 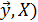объясняется в модели (1) ее регрессором x. Всегда .

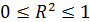Количественные характеристики взаимосвязи пары случайных переменных

Математическое ожидание (среднее значение), дисперсия и среднее квадратич.отклонение, ковариация и коэф-нт корреляции.

Матем. ожид. дискретн.

случ. перем. назыв. вел-на:M(x)=сумма(P_i*x_i),где M(x)-матем ожид. СДП х, P_i-вероятность появл. в опытах знач-я х_i,n-кол-во допустимых значений ДСВеличины. Матем. ожид-средневзвеш. значение ДСП,где в качестве веса использ значение вероятности.

Дисперсией дискретн случ перемен назыв. в-на:D²(x)=сумма(x_i-M(x))²*P(x_i), где D²(x)-дисперсия случ.перем.х. Дисперсия случ. вел-ны выступает в качестве характеристики разброса возможных ее значений. Положит. корень из дисперсии назыв средним квадратич.отклонением или стандартным отклонением,или стандартной ошибкой.

Матем.ожидание непрерывн. случ. перемен Хс законом распределения р_х(t) назыв. в-на:М(х)=интеграл от – бесконечности до + бесконечности tp_x(t)dt, что назыв. перв начальн.моментом ф-ции p_x(t).Через рез-ты наблюдений матем.ожид-е вычисл.:M(x)=(1/n)сумма(x_i).

Дисперсией непрерывн.случ. перемен. Хс функцией плотности вероятности p_x(t) назыв. выраж-е: D²(x)= интеграл от – бесконечности до + бесконечности(t-M(x))²p_x(t)dt,что назыв вторым центр моментом ф-ции p_x(t).В общем случае дисперсия случ.перем.: D²(x)=М(х-М(х))²=М(х²)-М²(х).

Ковариацией двух случ.перем. ХиУ:COV(x,y)=M((x-M(x))(y-M(y))).Значение ковариации отраж.наличие связи между 2 случ.перем.Если COV(x,y)>0,связь между XиY положит.,если <0-отрицат., если=0,X и Y-независ.перемен.Область возможн.знач. ковариации-вся числовая ось. Недостатки устраняются путем деления знач ковариации на знач стандартн отклонений перемен,что назыв коэф-нтом корреляции.это безразмерн вел-на,предел от -1 до 1 включительно.Ф-ла:р(х,у)=COV(x,y)/(D(x)*D(y)).