Раздел «Линии с распределенными параметрами».

1. Параметры кабельной линии: r₀ =1 Ом/км; g₀ = 0; wC₀ = 0,4 мСм/км; wL₀ = 0, w = 1000 рад/с.

Определить длину волны l, фазовую скорость волны в линии, волновое сопротивление Z_C, коэффициент затухания a и коэффициент фазы b линии.

3%

2. Определить параметры L₀ и С₀ воздушной линии без потерь, если ее волновое сопротивление Z_С = 300 Ом, а фазовая скорость 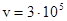км/с.

3%

3. Телефонная неискажающая линия длиной l =100 км при частоте f = 1600 Гц имеет входное сопротивление при холостом ходе 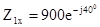Ом и при коротком замыкании 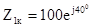Ом.

Определить первичные параметры линии r₀, L₀, g₀, C₀.

4%

4. Телефонная линия имеет волновое сопротивление 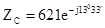Ом и коэффициент распространение 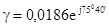1/км при w = 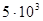рад/с.

Определить первичные параметры линии r₀, L₀, g₀, C₀.

4%

5. При каких условиях отношение напряжения в начале линии к напряжению в конце 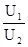равно отношению токов 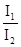в начале и в конце линии?

4%

6. Экспериментально установлено, что мощность передающего телефонного аппарата составляет 1 мВт, а мощность, подводимая к приемному телефонному аппарату, не должна быть меньше 1 мкВт. Полагая, что сопротивление телефонного аппарата согласовано с линией, определить отношение действующих значений напряжений в начале и в конце линии. Определить допустимую дальность связи по линии с коэффициентом затухания a =2,44 мНп/км.

4%

7. Двухпроводная линия длиной l = 100 км нагружена на волновое сопротивление 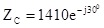Ом. В точке а, удаленной от конца линии на 20 км, напряжение в линии определяется выражением 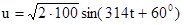В. Мгновенное значение тока в точке b, удаленной от конца линии на 40 км, равно 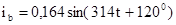А.

Определить коэффициент распространения g.

4%

8. Телефонный кабель имеет первичные параметры: r₀ = 12Ом/км, L₀ = 0,6 мГ/км, g₀ = 1мкСм/км, С₀ = 43 нФ/км. Кабель работает в режиме согласованной нагрузки при частоте f = 1 кГц.

Определить длину l участка кабеля, на котором затухание равно одному неперу; на котором токи и напряжения изменяют свою фазу на 360⁰.

4%

9. Определить коэффициент отражения волны напряжения q_u в конце линии с волновым сопротивлением Z_C при нагрузке линии на сопротивление Z₂ = Z_C; Z₂ = 0,5Z_C.

4%

10. Телефонная линия характеризуется параметрами: r₀ = 5,5Ом/км; L₀ = 2 мГ/км; g₀ = 0,5мкСм/км; С₀ = 6 нФ/км.

Определить значение индуктивности L, которую надо включить на каждый километр длины, чтобы линия стала неискажающей.

4%

11. Определить входное сопротивление Z_вх короткозамкнутой линии без потерь длиной в 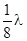(где l – длина волны). Волновое сопротивление линии Z_C.

4%

12. Определить входное сопротивление Z_вх линии без потерь при холостом ходе длиной в 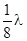(где l – длина волны). Волновое сопротивление линии Z_C.

4%

13. Определить, на каком минимальном расстоянии должна быть закорочена линия без потерь с волновым сопротивлением Z_C, чтобы ее входное сопротивление стало равным jZ_C.

4%

14. Линия без потерь имеет длину l, волновое сопротивление Z_C, коэффициент фазы b. В конце линии включена индуктивность L₂. Найти, на каком расстоянии х от конца линии будет ближайшая пучность напряжения, если напряжение в конце линии u₂ = U_2msinwt.

4%

15. Двухпроводная линия длиной l = 100 км имеет при частоте w = 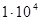рад/с вторичные параметры: Z_C = 300 О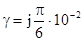м, 1/км.

Определить значения индуктивности L и емкости С П–образной схемы замещения линии.

4%

16. Длина двухпроводной линии без потерь меньше четверти длины волны. При нагрузке линии на активное сопротивление r₂ отношение действующих значений напряжений в начале и в конце линии 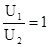, а при холостом ходе – 0,5.

Определить входное сопротивление линии Z_вх при коротком замыкании на конце.

4%

17. Трехфазная воздушная линия электропередачи характеризуется вторичными параметрами на фазу: Z_C = 390 Ом, gl = j1,05. На конце линии включена трехфазная активно–индуктивная нагрузка, потребляющая мощность Р₂ = 100 МВт при cosj₂ = 0,9. Линейное напряжение в конце линии U₂ = 380 кВ.

Определить величину линейного напряжения U₁ и тока I₁ в начале линии.

4%

18. Однородная линия без потерь с волновым сопротивлением Z_C, волновой скоростью v и длиной l на конце замкнута накоротко. Линия подключается к источнику ЭДС U₀.

Определить напряжение u и ток i в конце линии через время 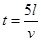после момента включения.

8%

19. Однородная линия без потерь с волновым сопротивлением Z_C, волновой скоростью v и длиной l разомкнута на конце. Линия подключается к источнику ЭДС U₀.

Определить напряжение u и ток i в конце линии через время 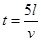после момента включения.

8%

20. Воздушная линия без потерь длиной l = 90 км с волновым сопротивлением Z_C = 400 Ом, волновой скоростью 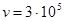км/с разомкнута на конце. Линия подключается к источнику постоянного напряжения U₀ = 120 кВ.

Определить напряжение u и ток i в линии через 1,2 мс после момента включения.

8%

21. Кабельная линия без потерь длиной l = 12 км с волновым сопротивлением Z_C = 60 Ом, волновой скоростью 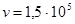км/с замкнута накоротко на конце. Линия подключается к источнику постоянного напряжения U₀ = 15 кВ.

Определить напряжение u и ток i в линии через 240 мкс после коммутации.

8%

22. Волна напряжения u_пад переходит с линии с волновым сопротивлением Z_С1 = 3Z_С на линию с волновым сопротивлением Z_С2 = Z_С (обе линии однородны и без потерь).

Определить коэффициент преломления k_u волны напряжения и коэффициент преломления k_i волны тока в месте соединения линий.

6%

Контрольные задания

2.1. Контрольное задание № 1.

Задача 1. Дана электрическая цепь, в которой происходит коммутация. В цепи действует постоянная ЭДС Е. Параметры цепи приведены по вариантам в таблице 2.1. Требуется определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения на каком–либо элементе или между заданными точками схемы.

Задачу следует решить двумя методами: классическим и операторным. На основании полученного аналитического выражения построить график изменения искомой величины в функции времени в интервале от t = 0 до t = 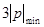, где 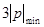– меньший по модулю корень характеристического уравнения.

Таблица 2.1.

Исходные данные по вариантам к задаче 1

контрольного задания 1.

Вариант	Рисунок	Е, В	L, мГн	С, мкФ	R1	R2	R3	R4	Определить
Ом
	2.5								i
	2.2								i1
	2.19								i1
	2.10								i1
	2.3								i1
	2.1								i1
	2.11								i1
	2.18								i3
	2.4								uC
	2.17								uC
	2.20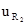
	2.15								uC
	2.6			2,5					uC
	2.7								i1
	2.12								i1
	2.16								i1
	2.8								i1
	2.13								i1
	2.9								i1
	2.14								i1
	2.5								uL
	2.2								i2
	2.19								i3
	2.10								i2
	2.3								uC
	2.1								i
	2.11								i3
	2.18								i1
	2.4								uL
	2.17								i2
	2.20								i1
	2.15								uL
	2.6			2,5					i3
	2.7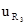
	2.12								uL
	2.16								i2
	2.8								i2
	2.13								i3
	2.9								i2
	2.14								i2

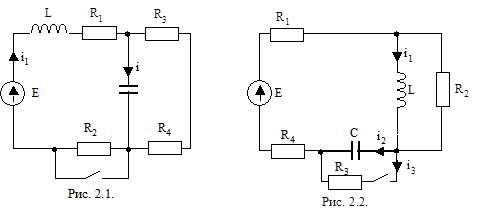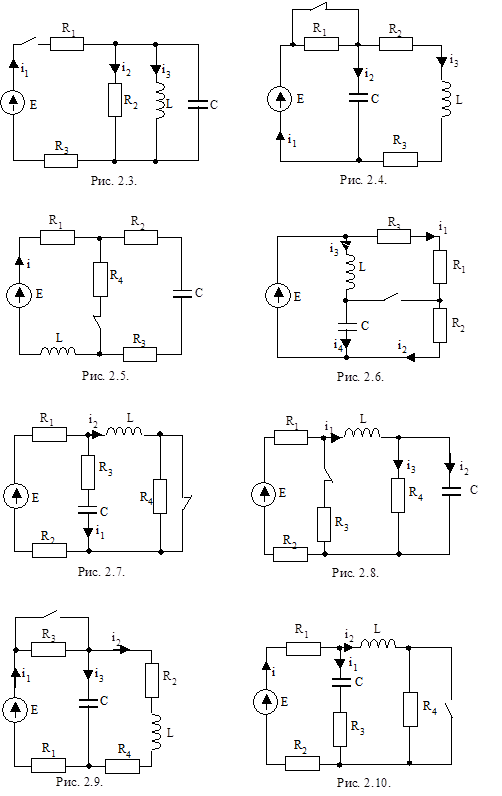
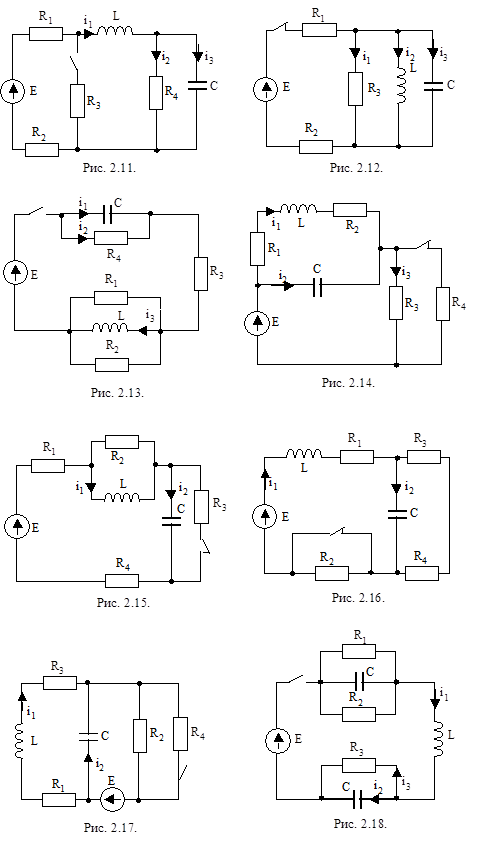
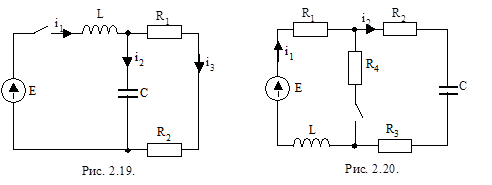
Рисунки к вариантам задачи 1 контрольного задания 1.

Задача 2. Дана электрическая схема, на входе которой действует напряжение, изменяющееся во времени по данному закону u₁(t). Требуется определить закон изменения во времени тока в одной из ветвей схемы или напряжение на заданном участке схемы. В таблице 2.2 в соответствии с номером варианта указан номер рисунка, на котором приведен график изменения во времени входного напряжения Параметры цепи R, L, C заданы в буквенном виде.

Задачу требуется решить с помощью интеграла Дюамеля. Искомую величину следует определить (записать ее аналитическое выражение) для всех интервалов времени. В зависимости от условий задачи полный ответ будет содержать два или три соотношения, каждое из которых справедливо лишь в определенном диапазоне времени.

В каждом ответе следует выполнить приведение подобных членов относительно 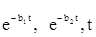и выделить постоянную составляющую.

Примечание. На рис. 2.31, 2.32, 2.36 входное напряжение дано с двумя индексами. Первый индекс (индекс 1) указывает на входное напряжение, второй индекс ( 1 или 2) – на интервал времени, о котором идет речь. Так, например, u₁₁ – входное напряжение для первого интервала времени, u₁₂ – входное напряжение для второго интервала времени.

Таблица 2.2

Исходные данные по вариантам к задаче 2

контрольного задания 1.

	Вариант	Рисунок с изображением схемы	Рисунок с графиком	Определить	Вариант	Рисунок с изображением схемы	Рисунок с графиком	Определить
	2.23	2.27	i4		2.23	2.28	i4
	2.22	2.27	uR		2.22	2.30	uR
	2.24	2.27	u2		2.24	2.30	u2
	2.23	2.29	i1		2.23	2.30	i1
	2.21	2.27	i1		2.21	2.28	i1
	2.22	2.28	i2		2.22	2.29	i2
	2.24	2.31	i1		2.24	2.32	i1
	2.25	2.27	i1		2.25	2.31	i1
	2.25	2.30	i2		2.25	2.32	i2
	2.21	2.28	uL		2.21	2.29	uL
	2.24	2.27	i3		2.24	2.30	i3
	2.22	2.27	i3		2.22	2.35	i3
	2.25	2.27	i3		2.25	2.30	i3
	2.22	2.27	uC		2.22	2.30	uC
	2.25	2.28	uL		2.25	2.29	uL
	2.24	2.28	i2		2.24	2.29	i2
	2.23	2.34	uC		2.23	2.30	uC
	2.26	2.31	u2		2.26	2.36	u2
	2.23	2.27	i2		2.23	2.34	i2
	2.23	2.27	i3		2.23	2.28	i3

Рисунки к вариантам задачи 2 контрольного задания 1.

2.2. Контрольное задание № 2.

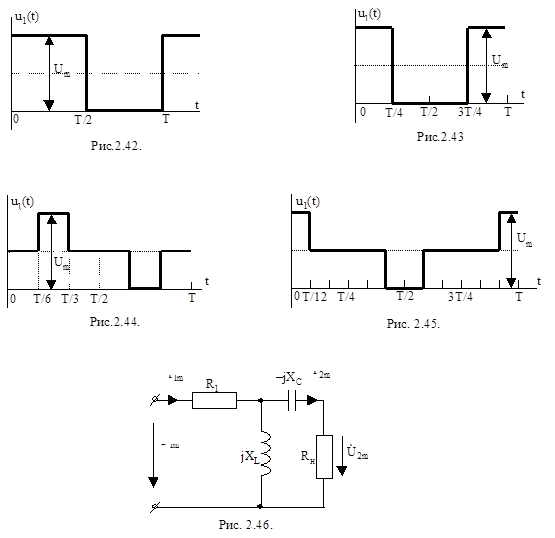
Задача 1. На рис.2.37 даны схемы, на вход которых воздействует одно из периодических напряжений u(t) (графики напряжений приведены на рис. 2.38 – 2.45). Схемы нагружены на активное сопротивление нагрузки R_н. Численные значения напряжения U_m, периода Т, параметров схемы L, C и величины активного сопротивления нагрузки R_н приведены в таблице 2.2. Требуется:

1. Разложить напряжение u(t) в ряд Фурье до пятой гармоники включительно, используя табличные разложения, приведенные в учебниках, и пояснение, имеющееся в указаниях к данной задаче.

2. Обозначив сопротивления элементов схемы в общем виде как R_н, jX_L, –jX_С, вывести формулу для комплексной амплитуды напряжения на нагрузке 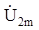через комплексную амплитуду входного напряжения 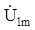. Полученное напряжение пригодно для каждой гармоники, только под X_L и X_C следует понимать сопротивления для соответствующей гармоники.

3. Используя формулы п. 2, определить комплексную амплитуду напряжения на выходе (на нагрузке) для следующих гармоник ряда Фурье: для нулевой, первой и третьей гармоник в схемах рис. 2.37,в,г; для первой, третьей и пятой гармоник в схемах рис. 2. 37,а.б.

4. Записать мгновенное значение напряжения на нагрузке u₂ = f(wt) в виде ряда Фурье.

У к а з а н и е:

На примере рис. 2.44, 2.45 покажем как осуществляется разложение в ряд Фурье кривых, которые имеют постоянную составляющую и начало которых сдвинуто во времени по отношению к табличным кривым. Прежде всего выделим в напряжении u₁(t) (рис.2.45) постоянную составляющую U_m/2 и мысленно проведем новую ось времени на высоте U_m/2. Тогда относительно новой оси времени оставшуюся часть напряжения запишем в виде

.

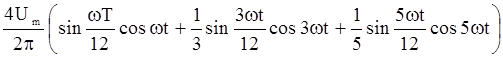Здесь под U_m понимается амплитуда заданного напряжения, а угол wТ/12 равен углу, обозначенному в учебниках a. С учетом постоянной составляющей u₁(t) (рис 2.45) раскладывается в ряд Фурье следующим образом:

u₁(t) = .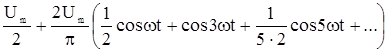

График напряжения u₁(t) (рис.2.44) на время Т/4 смещен (запаздывает) во времени, поэтому для рис. 2.44

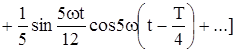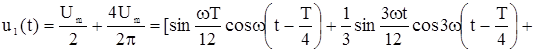
или

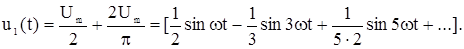
Покажем, как вывести формулу для напряжения на выходе схемы 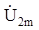через параметры схемы и напряжение на входе 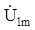на примере рис.2 46. Запишем уравнение по второму закону Кирхгофа:

.

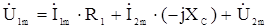Выразим ток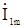и и 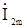через напряжение :

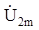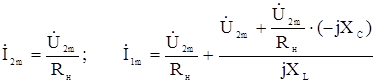
и подставим в исходное выражение, тогда

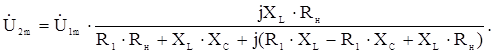
Таблица 2.2.

Исходные данные по вариантам к задаче 1 контрольного задания 2.

Вариант	L, мГн	С, мкФ	Т, 10-3 с	Um, В	Rн Ом	Рисунок с изображением схемы	Рисунок с графиком u1(t)
	1,44	0,8	0,48		35,4	2.37,б	2.43
					65,7	2.37,в	2.42
	0,5	0,4	0,167			2.37,г	2.41
	0,4	0,5	0,159		36,4	2.37,а	2.39
	0,7	0,24	0,134		41,4	2.37,б	2.40
			0,625		86,5	2.37,в	2.43
	5,6	2,28	1,2	48,5	38,6	2.37,г	2.42
	2,52	1,4	0,63			2.37,а	2. 42
	4,2	1,44	0,8		41,4	2.37,б	2.41
			1,67			2.37,в	2.40
			0,314			2.37,г	2.43
			5,88			2.37,а	2.43
	1,5	0,3	0,354		64,5	2.37,б	2.38
	2,58	1,43	0,483		49,6	2.37,в	2.45
		0,9	0,565		44,7	2.37,г	2.38
	5,4		1,34		55,2	2.37,а	2.44
	6,25	12,4	3,13	12,78	17,5	2.37,б	2.39
	6,25		2,5		31,5	2.37,в	2.40
	0,5	0,4	0,167			2.37,г	2.43
	0,7	0,875	0,277		36,4	2.37,а	2.41
	1,6	0,89	0,536		35,4	2.37,б	2.39
	9,57	3,48	1,74	18,85	65,7	2.37,в	2.38
	0,55	0,44	0,184	104,6		2.37,г	2.38
	0,357	0,447	0,142	33,4	36,4	2.37,а	2.41
	0,62	0,212	0,118		41,4	2.37,б	2.38
	4,35	0,87	0,544		86,5	2.37,в	2.39
	6,15	2,5	1,33	26,2	38,6	2.37,г	2.40
	2,9	1,61	0,725			2.37,а	2. 44
	2,92		0,555		41,4	2.37,б	2.39
		1,15	1,92	13,35		2.37,в	2.44
	1,15	1,15	0,362	102,2		2.37,г	2.39
	16,7	6,67	4,9	104,5		2.37,а	2.41
	1,72	0,334	0,416		64,5	2.37,б	2.40
	1,95	1,08	0,365		49,6	2.37,в	2.43
	3,6	1,08	0,678	37,5	44,7	2.37,г	2.40
	5,94	3,3	1,47		55,2	2.37,а	2.40
	5,68	11,27	2,84		17,5	2.37,б	2.39
	6,87		2,75		31,5	2.37,в	2.42
	0,625	0,5	0,209	44,7		2.37,г	2.43
	0,65	0,81	0,257		36,4	2.37,а	2.43

Рисунки к вариантам задачи 1 контрольного задания 2.

Задача 2.По данным, помещенным в таблице 2.4, выполнить следующее:

Рассчитать магнитную цепь методом двух узлов и определить величины, указанные в крайнем справа столбце этой таблицы.

По результатам, полученным в п. 1, найти магнитное напряжение между двумя точками магнитной цепи, вычислив его один раз по пути, заданному ниже (п. 1 «указаний к выбору варианта»), и другой раз по любому иному пути, выбранному по своему усмотрению. Полученные результаты срав­нить между собой.

Для принятых в п. 1 положительных направлениях магнитных потоков и заданного направления МДС составить систему уравнений по законам Кирхгофа.

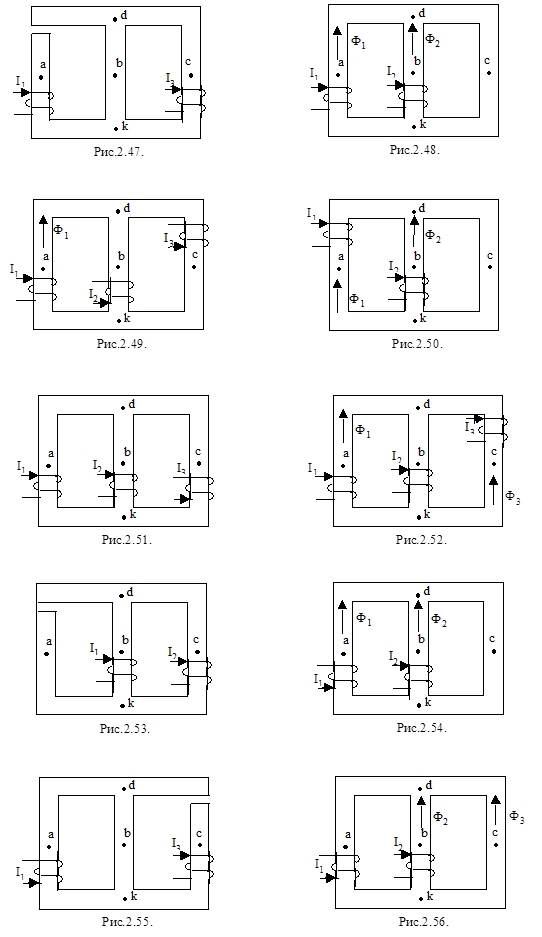
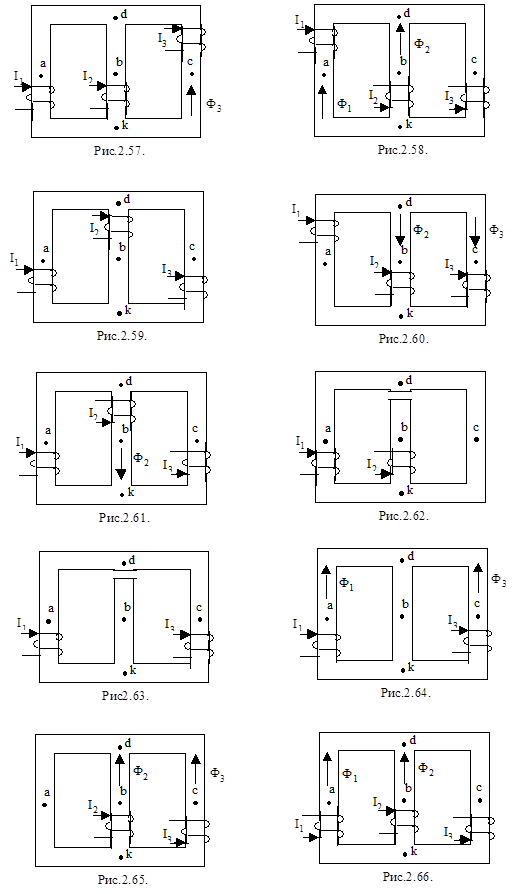
Схематические изображения магнитопроводов с размещением намагничи­вающих катушек, способа их намотки на сердечник и положительных на­правлений токов в них приведены на рис. 2.47 – 2.66.Точки а,б,с находятся посередине каждого участка магнитопровода.

На рис. 2.47, 2.54 направление тока изменить на противоположное.

Указания к выбору варианта.

Для студентов, фамилии которых начинаются с букв А, В, И, М, Х, Ю, следует определить указанное в п. 2 магнитное напряжение U_akb; с букв Б, Г, Д , Е, З – U_dak; с букв Ж, К, Н, Ф, Э – U_сkb; с букв П, Р, Ч, Ш, Ц, Я – U_akс; с букв Л, О, С, Т, У, Щ – U_bkcd.

Здесь U_akb – магнитное напряжение между точками а и b по пути a – k – b; U_dak магнитное напряжение между точками d и k по пути d – a –k и т.д.

В таблице 2.5 приняты следующие обозначения: l – длина средней магнит­ной линии одной ветви магнитной цепи; l_d – длина воздушного зазора (его положение в магнитной цепи дано на схемах магнитопроводов); S – cечение участков магнитопровода; w – число витков катушек; I – постоян­ный ток в катушке.

Обозначения величин даются с индексами, которые указывают, к какой ветви магнитной цепи относится та или иная величина; индекс 1 – к левой магнитной ветви, индекс 2 – к средней ветви, индекс 3 – к правой ветви.

Магнитные свойства стали, из которой изготовлены магнитопроводы, определяются кривой намагничивания, приведенной ниже.

Магнитные свойства стали

Н,А/м
В, Тл	0,22	0,75	0,93	1,02	1,14	1,28	1,47	1,53	1,57	1,6

Таблица 2.4

Исходные данные по вариантам к задаче 2 контрольного задания 2 контрольного задания 2.

	Ва­риант	Ри­сунок	Дано	До­пол­ни­тель­ные усло­вия	Оп­реде­лить
	l1, см	S1, см2	w1	I1, A	l2, см	S2, см2	w2	I2, A	l3, см	S3, см2	w3	I3, A	ld, мм
	2.47				1,1		6,06				4,05			0,5		Ф1, Ф2
	2.48		5,7		0,6		3,9				9,5				Ф1 = Ф2	Ф1, I2
	2.51				0,3						5,6		0,21		Ф2 = 0	Ф3, I2
	2.52		7,6		0,21				0,05		11,3				Ф3 – Ф1 = 20	Ф1, I3
	2.55		15,4				10.4						0.5			Ф1, Ф2
	2.56				0,5		14,2		0,3		13,7				Ф3 = Ф2	w2, Ф1
	2.59		3,9				4,8		0,1		4,6		0,2		Ф2 = 0	w2, Ф3
	2.60		7,9		0,1		4,8		0,05		4,4				Ф2 – Ф3 = 20	Ф2, I3
	2.63				0,65								0,575	1,25		Ф1, Ф2
	2.64				0,7										Ф1 = Ф3	Ф3, I1
	2.49								0,04		1,2		0.1		Ф1 = 25	Ф2, I2
	2.50				0,2										Ф2 – Ф1 = 20	Ф1, I3
	2.53								0,2		1,78		0.3	0,1		Ф3, Ф2
	2.54		5,3		0,5				0,2		10,2				Ф1 = Ф2	w2, Ф1
	2.57				0,1				0,25						Ф3 = 98	Ф2, I3
	2.58		3,8		0,25		7,6				10,1		0,5		Ф2 – Ф1 = 20	Ф1, I2
	2.61		7,2		0,47		4,6		0,1		2,9		0,2		Ф2 = 70	Ф1, w2
	2.62				0,1				0,7					0,52		Ф1, Ф2
	2.65								0,4						Ф3 = Ф2	Ф3, I2
	2.66				0,05		7,8		0,2				0,1		Ф2 – Ф1 = 30	w2, Ф1
	2.47				1,52								2,5	0.1		Ф1, Ф2
	2.48		6,15		0,3		4,2								Ф1 = Ф2	Ф3, I2
	2.51		4,3		0,1						4,8		0,42		Ф2 = 0	Ф3, I2
	2.52		7,3			11,5	12,3		0,3	22,5					Ф3 – Ф1 = 20	Ф1, I3
	2.55		14,4		0,75		10,5									Ф3, Ф2
	2.56				0,4				0,3						Ф3 = Ф2	w2, Ф3
	2.59		4,2		0,5		4,8		0,1	4,9	4,9		0,5		Ф2 = 0	w2, Ф1
Продолжение таблицы 2.4.
	Ва­ри­ант	Ри­су­нок	Дано	Дополни­тельные ус­ловия	Опреде­лить
	l1, см	S1, см2	w1	I1, A	l2, см	S2, см2	w2	I2, A	l3, см	S3, см2	w3	I3, A	ld, мм
	2.60		8,1		0,15	6,5	5,1		0,1	3,2	3,2				Ф2 – Ф3 = 20	Ф1, I3
	2.63													1,25		Ф3, Ф2
	2.64		25,3		0,5					45,5	45,5				Ф1 = Ф3	Ф3, I3
	2.49		1,95			3,5	0,96		0,05	1,25	1,25		0,3		Ф1 = 25	Ф2, I1
	2.50		2,9		0,25		4,75			8,33	8,33				Ф2 –Ф1 = 20	Ф1, I2
	2.53		7,5			4,32	1,9			1,75	1,75		0,5	0,1		Ф1, Ф3
	2.54		5,6		0,2					8,9	8,9				Ф1 = Ф2	Ф3, I2
	2.57		7,95		0,5	11,5	13,8			7,1	7,1				Ф3 = 98	Ф2, I3
	2.58		3,9		0,5		6,8			9,9	9,9		0.25		Ф2 – Ф1 = 20	Ф2, I2
	2.61				0,1				0,1						Ф2 = 70	w2, Ф3
	2.62				0,4				1,4					0,57		Ф3, Ф2
	2.65		11,9				11,5		1,1	9,1	9,1				Ф3 = Ф2	Ф1, I3
	2.66		9,3		0,07		7,7		0,2	15,5	15,5		0,7		Ф2 – Ф1 = 30	w2, Ф2

Рисунки к вариантам задачи 2 контрольного задания 2.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.

Основная литература

1. Бессонов Л.А. Теоретические основы электротехники: Электриче­ские цепи. –М.: Высшая школа, 1978. –528 с.

2. Теоретические основы электротехники / Под редакцией П.А. Ион­кина. – М.: Высшая школа, 1982. –544 с.

2. Основы теории цепей / Под редакцией П.А. Ионкина. – М.: Энер­гоатомиздат, 1989. –527 с.

4. Нейман Л.Р., Демирчан К.С. Теоретические основы электротех­ники, том 1. – М. – Л.: Энергия, 1981. –533 с.

5. Атабеков Г.И. Теоретические основы электротехники, часть 1. –М.: –Энергия, 1978. –592 с.

6. Комлянский А.Е., Лысенко А.П., Полотовский Л.С. Теоретические основы электротехники. –Л.: Энергия. –1976. –526 с.

Дополнительная литература

7. Матханов П.Н. Основы анализа электрических цепей: Линейные цепи. –М.: Высшая школа, 1990. –399 с.

8. Шебес М.Р., Каблукова М.В. Задачник по теории линейных элек­трических цепей. М.: Высшая школа, 1990. –543 с.

9. Сборник программированных задач по теоретическим основам электротехники. Львов, Вища школа, 1976. –504 с.

10. Афанасьев В.В., Веселовский О.Н. Расчеты электрических цепей на программируемых калькуляторах. – М.: Энергоатомиздат. 1992. –189 с.

11. Сборник задач по теоретическим основам электротехники / Под редакцией Л.А. Бессонова: М.: Высшая школа, 1980. –472 с.

12. Задачник по теоретическим основам электротехники / Под редак­цией Т.Ю. Могилевской: Томск, Издательство томского университета. –1972. –196 с.

12. Гольдин О.Е. Задачник по теории электрических цепей. –М.: Выс­шая школа. 1969. –312 с.

Приложение:

Образец титульного листа контрольного задания

Министерство общего и профессионального образования РФ

Якутский государственный университет им. М.К. Аммосова

Геологоразведочный факультет

Кафедра «Электроснабжение»

КОНТРОЛЬНОЕ ЗАДАНИЕ

по курсу

«Теоретические основы электротехники» ч. II.

Выполнил студент 2 курса

Иванов И.И.

14.02.98 г.

Проверил Петров П.П.

1998 год

ОГЛАВЛЕНИЕ

Предисловие 3

1. Задачи рейтингового контроля 5

1.1. Раздел «Несинусоидальные токи в линейных цепях» 5

1.2. Раздел «Переходные процессы в электрических цепях» 9

1.2. Раздел «Нелинейные цепи постоянного тока» 14

1.4. Раздел «Магнитные цепи» 19

1.5. Раздел «Линии с распределенными параметрами» 24

2. Контрольные задания 27

2.1. Контрольное задание № 1 27

2.2. Контрольное задание № 2 33

Рекомендуемая литература 43

Приложение: образец титульного листа контрольного

задания 44