Изучение вынужденных колебаний

КРАТКАЯ ТЕОРИЯ. Вынужденными колебаниями называются колебания, происходящие под действием периодически изменяющейся внешней (вынуждающей) силы. Если первоначально колебательная система находилась в состоянии покоя, то под действием вынуждающей силы она выйдет из этого состояния. Часть энергии колебательного движения будет затрачиваться на преодоление сил сопротивления. По мере увеличения амплитуды колебаний эта часть возрастает и наступит момент, когда работа, совершаемая вынуждающей силой, станет равной убыли энергии колеблющегося тела. Начиная с этого момента, амплитуда перестанет увеличиваться, и колебания станут установившимися.

В простейшем случае вынуждающая сила изменяется по гармоническому закону:

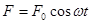. (1)

Тогда установившиеся колебания являются гармоническими, и их частота равна частоте изменения вынуждающей силы.

Пусть на колеблющееся тело массой 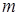действуют возвращающая сила:

,

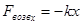сила сопротивления среды:

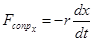
и вынуждающая сила

.

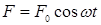Дифференциальное уравнение движения этого тела запишем согласно второму закону Ньютона в виде:

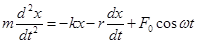(2)

или, введя обозначения: 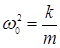и 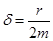, получим:

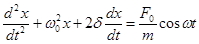, (3)

где 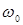- собственная частота колебательной системы, 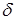- коэффициент затухания, 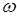- циклическая частота вынуждающей силы.

Решение этого уравнения имеет вид:

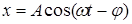, (4)

где 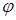- сдвиг фаз между силой и вызываемыми ею колебаниями. Подставив в уравнение (3) выражение (4), а также первую и вторую производные от него, получим:

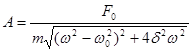(5)

Из выражения (5) видно, что амплитуда установившихся вынужденных колебаний зависит от частоты изменения вынуждающей силы и при некотором её значении, близком к частоте собственных колебаний, достигает максимума.

Явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний называется резонансом. Соответствующая резонансу частота вынуждающей силы носит название резонансной частоты w_рез. В нашем случае:

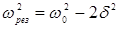, (6)

амплитуда вынужденных колебаний при резонансе:

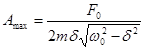. (7)

Из выражения (7) в частности следует, что в отсутствии затухания ( 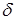= 0) амплитуда при резонансе должна была бы обращаться в бесконечность. Однако при больших амплитудах колебания перестают быть гармоническими, поэтому исходное уравнение (2) невозможно использовать для их описания.

Если же коэффициент затухания мал по сравнению с угловой частотой собственных колебаний системы:

,

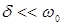то резонансная частота весьма близка к частоте собственных колебаний:

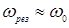(8)

и амплитуда при резонансе может быть выражена в виде:

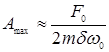. (9)

График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной кривой и представлен на рис. 1. Кривые построены для систем с одинаковой частотой собственных колебаний и различными значениями коэффициента затухания. Видно, что по мере его возрастания максимальная амплитуда уменьшается, а резонансная частота сдвигается в область малых частот в соответствии с выражением (6).

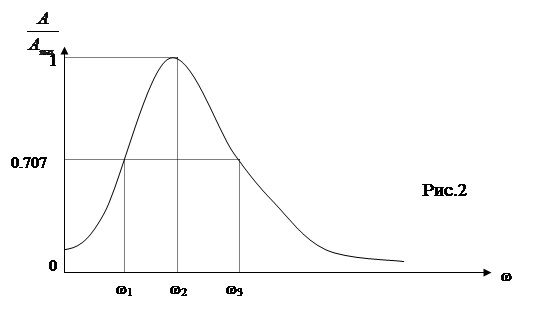Рассчитаем так называемую ширину резонансной кривой 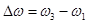для энергии колеблющегося тела, равной половине энергии его колебаний на частоте резонанса (рис. 2). Так как энергия осциллятора пропорциональна квадрату амплитуды, уменьшение энергии в два раза соответствует уменьшению амплитуды колебаний до уровня 0,707 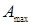. В случае малого затухания резонансная амплитуда определяет­ся соотношением (9). На произвольной частоте амплитуда вынуж­денных колебаний рассчитывается согласно (5), которые отличают­ся друг от друга только знаменателями. Энергия осциллятора на частотах 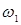и 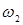должна быть равна половине его энергии на резонансной частоте 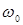, это означает, что:

.

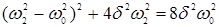Пренебрегая членами высшего порядка малости и учитывая, что при малом затухании справедливо (8) и 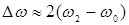, получаем:

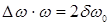
или

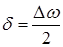. (10)

Коэффициент затухания характеризует рассеяние энергии осциллятором в единицу времени. Потери энергии за период колебаний определяются логарифмическим декрементом затухания. Эти величины связаны соотношением:

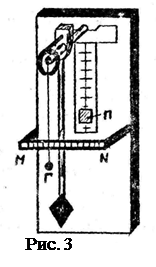
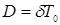, (11)

где 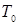- период собственных колебаний, связанный с угловой частотой:

.

Отметим, что соотношения (10) и (11) справедливы только в случае малого затухания колебаний.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Работа выполняется на установке с двумя маятниками (рис. 3). Один из них тяжелый, с большим запасом энергии и постоян­ным периодом колебаний Т, используется в качестве задающего вибратора. Другой маятник, более легкий, служит резонатором и раскачи­вается под действием толчков маятника вибратора.

Маятник-резонатор представляет собой небольшой груз Г, под­вешенный на нити. Эта нить проходит через канал в оси маятника-вибратора. На другом её конце подвешен противовес П. Противо­вес и трение нити о стенки канала оси позволяют достаточно надежно обеспечить заданную длину маятника-резонатора. В то же время это дает возможность легко изменять длину маятника-резонатора, подтягивая нить за груз на одном ее конце или за противовес на другом конце нити.

Измерения начинают с установки длины маятника-резонатора, соответствующей наименьшему значению на вертикальной шкале. За­тем отклонив маятник-вибратор до деления, указанного преподава­телем, его отпускают. Толчки маятника-вибратора раскачивают маятник-резонатор. Когда его амплитуда перестанет возрастать, произ­водят отсчет её значения на горизонтальной шкале по наибольшему отклонению нити маятника.

Во избежание ошибок за счет параллакса, глаз в момент от­счета нужно располагать перпендикулярно шкале. Измерения повторяют при различной длине маятника-резонатора.

Для построения резонансной кривой, кроме значе­ния резонансной амплитуды, нужно определить еще не менее пяти раз значения амплитуды при различных длинах резонатора до резонанса и не менее пяти значений амплитуды после него.

ЗАДАНИЕ

I. В условных делениях снять значения амплитуды колебаний маятника-резонатора и его длину, заполнив таблицу.

2. Построить на миллиметровой бумаге резонансную кривую, откладывая по оси абсцисс длину резонатора в условных де­лениях, а по оси ординат амплитуду его колебаний, также в условных делениях.

3. По 20 полным колебаниям определить период колебания вибратора Т и период колебаний маятника-резонатора, соответствую­щий максимальной амплитуде, рассчитать период, пренебрегая затуханием.