Краткая теория исследуемого явления. Электрическая цепь состоит из соединенных друг с другом источников электрической энергии и различных устройств (нагрузок)

Электрическая цепь состоит из соединенных друг с другом источников электрической энергии и различных устройств (нагрузок), по которым может протекать электрический ток.

Элементы электрических цепей характеризуются сопротивлением (R), емкостью (С) и индуктивностью (L).

В простейшем случае перечисленные параметры можно считать независящими от тока и напряжения. Такие элементы цепи называют линейными. Их достоинство в том, что процессы, происходящие в них, описываются линейными алгебраическими (дифференциальными) уравнениями. Соответственно такие электрические цепи называются линейными.

Электрическая цепь состоит из узлов и ветвей. Ветвью называют весь участок цепи между соседними узлами, в котором все элементы соединены последовательно. Узлом электрической цепи называют место соединения трех или большего числа ветвей. Любой замкнутый путь, проходящий по нескольким ветвям, называют контуром электрической цепи.

Расчет сложных (разветвленных) цепей постоянного тока заключается в отыскании токов по заданным сопротивлениям участков цепи и действующим в них ЭДС. При расчете электрических цепей (в качестве одного из методов) используются два правила Кирхгофа.

Первое правило Кирхгофа применяется к узлам электрической цепи: алгебраическая сумма токов в узле равна нулю, т.е. SI_к=0. При составлении уравнений, согласно первому правилу Кирхгофа, необходимо произвольно выбрать направления токов во всех ветвях и обозначить их на схеме стрелками. Токи, входящие в узел, считаются положительными. Если число узлов n, то по первому правилу Кирхгофа можно составить n-1 уравнений (чтобы получить линейно независимые уравнения).

Первое правило Кирхгофа вытекает из закона сохранения электрического заряда, поэтому в каждом узле должны быть и входящие в него токи, и выходящие.

Второе правило Кирхгофа вытекает из закона Ома для неоднородного участка цепи в интегральной форме и применяется к контурам электрической цепи. Оно гласит: алгебраическая сумма падений напряжений в любом контуре равна алгебраической сумме ЭДС, действующих в этом контуре: SI_кR_к =SЕ_n.

Независимость уравнений при составлении их по второму правилу Кирхгофа будет обеспечена, если контуры выбирать так, чтобы каждый последующий отличался от предыдущего хотя бы одной новой ветвью. Если число ветвей p, то число независимых уравнений равно (p-n+1). Число уравнений, составленных по первому и второму правилу Кирхгофа, должно быть равно числу ветвей. При составлении уравнений по второму правилу Кирхгофа необходимо выбрать произвольно направление обхода контуров. При составлении суммы падений напряжений I_кR_к считается положительным, если выбранное направление тока совпадает с направлением обхода контура. ЭДС считают положительной, если при обходе контура она пересекается от "–" к "+" (направление возрастания потенциала внутри источника). Решая систему из (n-1)+(p-n+1)= p независимых уравнений, можно определить токи во всех p ветвях цепи, если известны ее параметры и ЭДС, действующие в этой цепи. Если в результате расчета некоторый ток окажется отрицательным 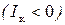, то этот ток в действительности направлен противоположно выбранному направлению.