Указания к решению задачи № 1

Для заданной расчетной схемы (рисунок 2.1) необходимо выполнить следующее:

1) построить эпюру изменения продольной силы N(x) по длине стержня;

2) определить размеры поперечного сечения из условия прочности на растяжение (сжатие), округлить полученные размеры до целого числа;

3) определить напряжения в поперечных сечениях стержня и построить эпюру их изменения по длине стержня;

4) определить абсолютную упругую деформацию стержня, приняв Е = 2,1×10⁵ МПа.

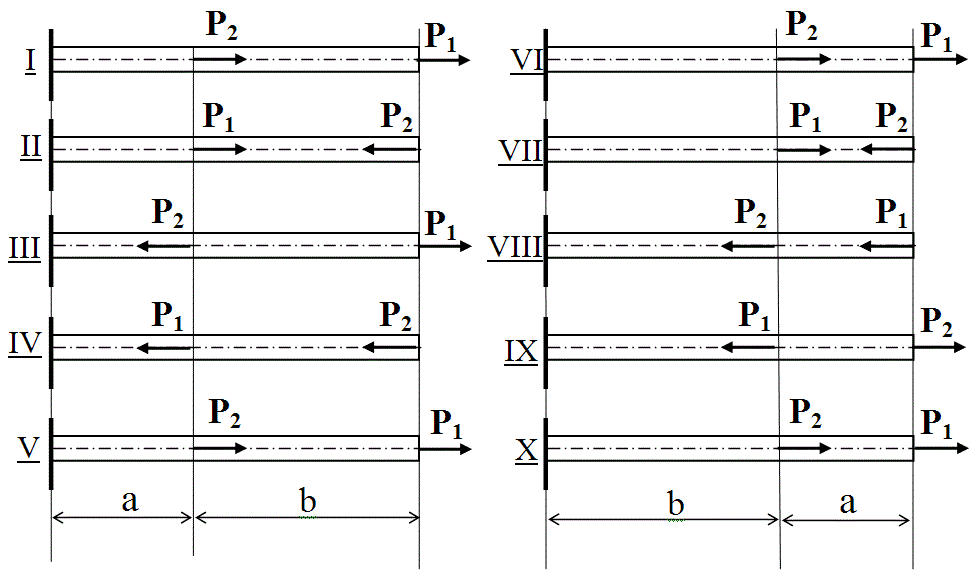
Рисунок 2.1

Таблица 2.1
Данные	Варианты
1	2	3	4	5	6	7	8	9	10
Р1, кН
Р2, кН
а, м	0,1	0,3	0,4	0,3	0,7	0,5	0,2	0,3	0,4	0,2
b, м	0,2	0,1	0,2	0,3	0,3	0,4	0,4	0,3	0,4	0,1
[σ], МПа
Форма сечения	квадрат	прямоугольник b/h = 0,4	круг

Пример решения задачи № 1

Исходные данные:

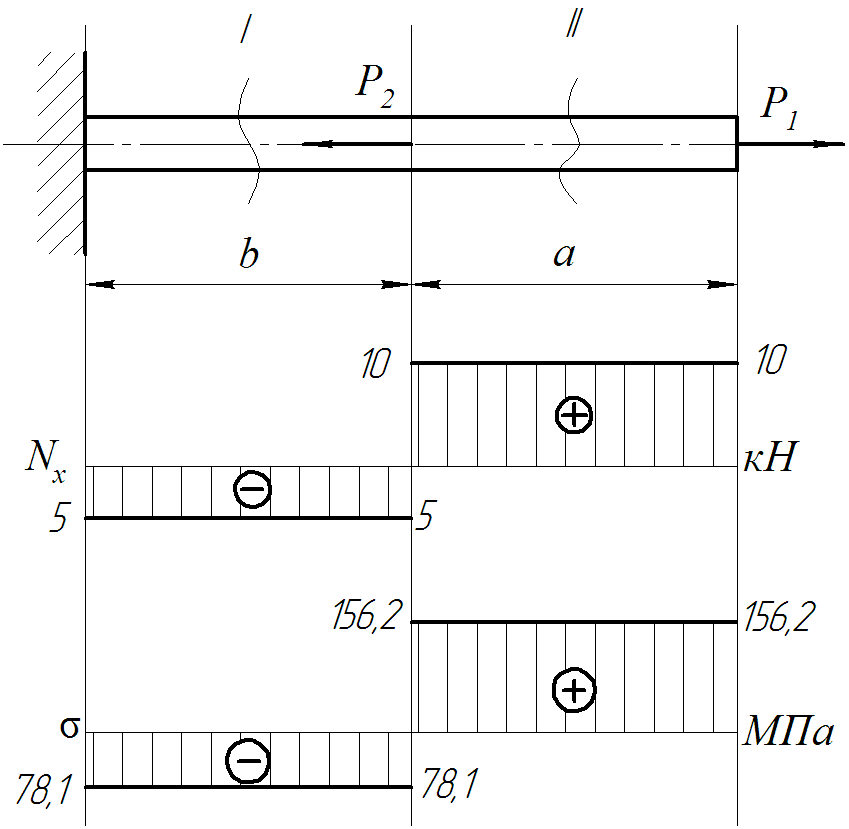P₁ = 10 кН

P₂ = 15 кН

a = 0,3 м

b = 0,2 м

[σ] = 200 МПа

форма сечения – квадрат

Стержень закреплен жёстко одним концом и к нему приложены две внешние силы P₁ и P₂, направление которых и точки их приложения совпадают с продольной осью стержня.

Стержень состоит из двух участков. Обозначим их, начиная с закрепленного конца, цифрами I и II.

1) Проведём на участке I произвольное сечение и рассмотрим равновесие правой отсеченной части:

N_I = P₁ − P₂= 10 − 15 = −5 кН

Знак перед числом говорит о том, что участок испытывает деформацию сжатия.

Проведём произвольное сечение на участке II. Определим нормальную (продольную) силу N_II:

N_II = P₁ = 10 кН

Данный участок испытывает деформацию растяжения.

Строим эпюру изменения продольной силы N(x) по длине стержня под расчетной схемой с соблюдением масштаба.

2) Определим размеры поперечного сечения из условия прочности при растяжении (сжатии):

,

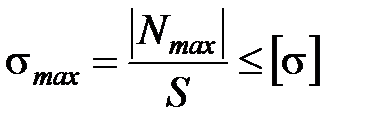откуда следует:

.

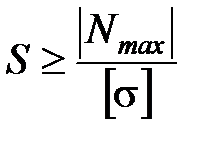Из эпюры продольной силы видно, что |N_max| = 10 кН. Следовательно,

.

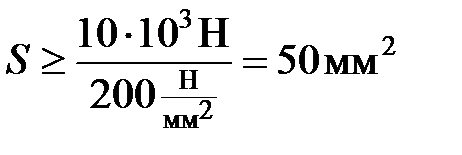Принимая из условия задачи, что сечение – квадрат, определяем его стороны: 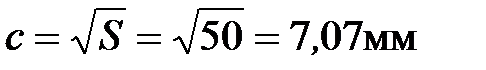. Округляем в сторону увеличения до целого числа, т.е. принимаем c = 8 мм. Тогда площадь поперечного сечения стержня будет равна S = c² = 8² = 64 мм².

3) Определим напряжения в поперечных сечениях стержня на обоих участках:

;

.

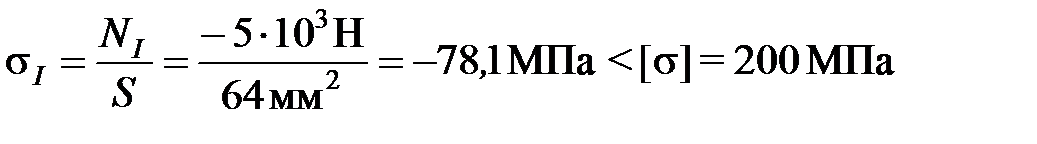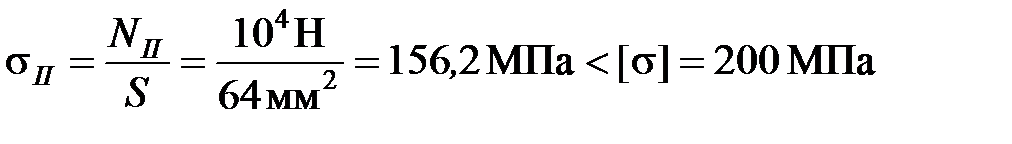Условие прочности выполняется.

Строим эпюру изменения напряжения растяжения (сжатия) по длине стержня под эпюрой продольной силы с соблюдением масштаба.

4) Определим абсолютную упругую деформацию стержня Δl = ΣΔl_i, в нашем случае

.

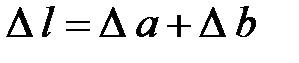Деформация на I участке равна:

;

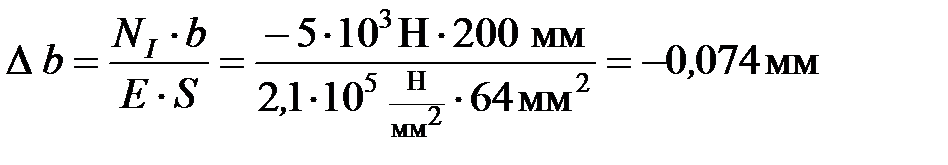деформация на II участке равна:

;

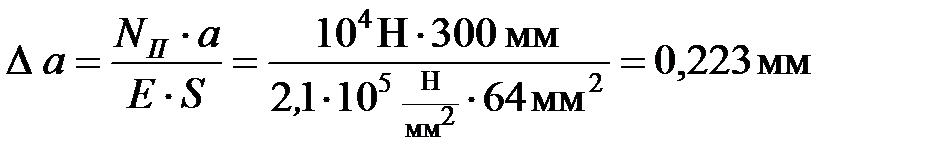таким образом, суммарная абсолютная упругая деформация стержня равна:

.

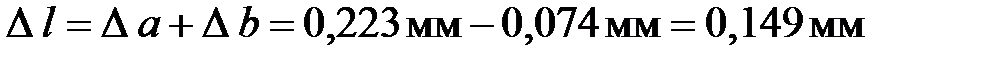Ответ:

c = 8 мм

σ_I = −78,1 МПа

σ_II = 156,2 МПа

Δl = 0,149 мм.

3. ЗАДАЧА №2. «Расчёт балки на прочность по нормальным напряжениям»

Изгибомназывают такой вид деформации бруса (стержня), при котором в поперечных сечениях возникает внутренний силовой фактор – изгибающий момент М_и. Брус, испытывающий деформацию изгиба, называется балкой.

Кроме изгибающего момента в поперечных сечениях балки могут возникать поперечные силы Q , в этом случае изгиб называют поперечным.

Если изгибающий момент является единственным внутренним силовым фактором (Q = 0), то изгиб называют чистым.

Если линии действия всех сил и пар сил (моментов), приложенных к балке, находятся в одной плоскости, совпадающей с главной центральной осью поперечного сечения (ось симметрии сечения, проходящая через его центр тяжести), то такой изгиб называют прямым или плоским (что имеет место в нашем случае), в противном случае изгиб называют косым.

При определении реакций в опорах двухопорных балок, нагруженных только поперечными силами, принимаем SХ º 0 ( см. рисунок 3.1)

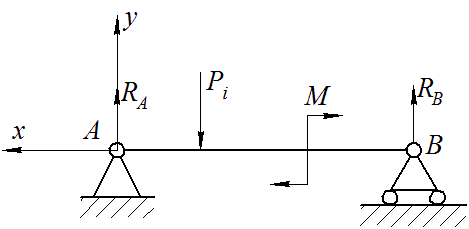
Рисунок 3.1

Таким образом, имеем две неизвестных по величине реакции R_A и R_В, которые определяем, составляя два уравнения:

ΣM(A) = 0;

ΣM(B) = 0;

откуда находим, соответственно, R_B и R_A. Для проверки найденных величин используем уравнение:

ΣY = 0;

Поперечная сила в любом сечении численно равна алгебраической сумме проекции всех сил, расположенных по одну сторону от сечения, на ось Y, при этом соблюдается правило знаков, изображённое на рисунке 3.2.

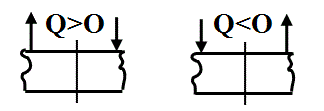
Рисунок 3.2

Изгибающий момент в любом сечении численно равен алгебраической сумме моментов всех сил, расположенных по одну сторону от сечения, относительно центра тяжести рассматриваемого сечения, и при этом соблюдается правило знаков, изображённое на рисунке 3.3.

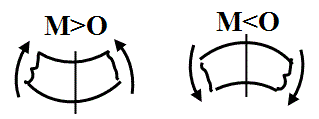
Рисунок 3.3

При построении эпюр внутренних силовых факторов Q(x) и M(x) следует использовать дифференциальные зависимост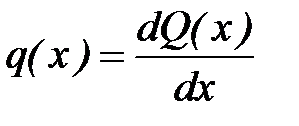и

и 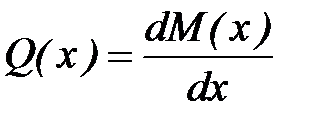(см. вывод [1], стр. 70-71.)

Функция поперечной силы Q(x) представляет собой производную от функции изгибающего момента M(x), благодаря чему можно найти точку экстремума функции M(x).

Рассмотрим два типичных случая построения эпюр поперечной силы и изгибающего момента (см. рисунки 3.4 и 3.5).

I случай: эпюра поперечной силы не пересекает нулевую линию (рисунок 3.4).

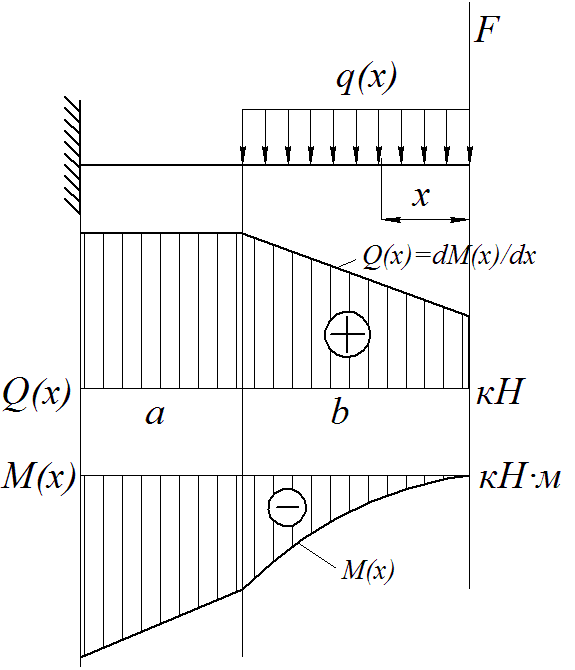
Рисунок 3.4

В этом случае значение момента определяем не менее, чем в трех точках:М(x=0); М(x=B/2); М(x=В); и по этим значениям строим кривую М(x).

II случай:эпюрапоперечной силы пересекает нулевую линию (рисунок 3.5).

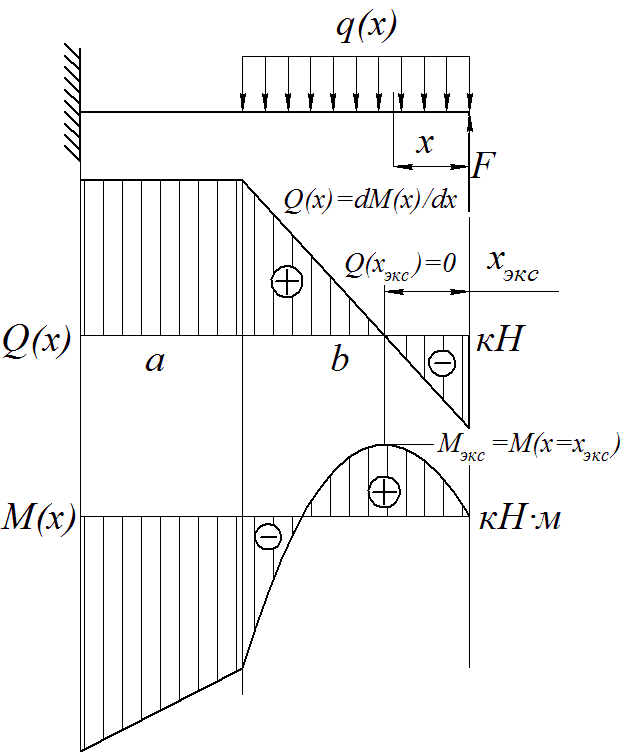
Рисунок 3.5

В этом случае определим момент при М(x=0); М(x=b), а точку, соответствующую вершине параболы, определяем, приравняв выражение Q(x) к нулю, откуда определяем значение х_экс, при котором Q(x_экс) = 0 и, подставив в выражение М(х), отмечаем точку вершины параболы М(x_экс).

Условие прочности балки по нормальным напряжениям для материалов, одинаково сопротивляющихся растяжению и сжатию ([σ]_сж= [σ]_р)

;

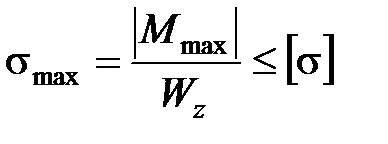откуда: .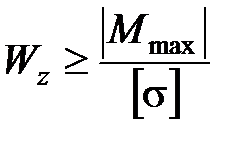

По полученному значению W_z определяем размеры поперечного сечения балки (швелера, двутавра и т.д.).

Формулы определения W_z для простейших фигур:

круг: ;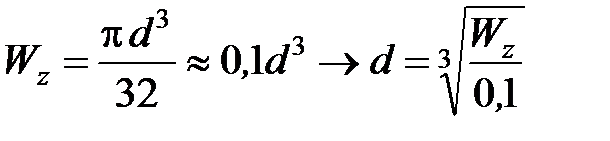

квадрат: 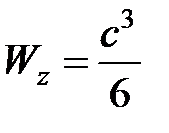, где c – сторона квадратного сечения ;

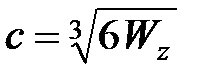прямоугольник: 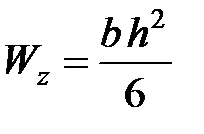; необходимо знать соотношение 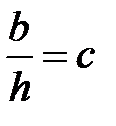, откуда получаем: .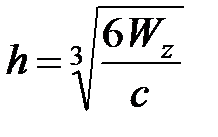