Глава 3. линейные дифференциальные системы

n-го ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

§1. Линейные дифференциальные системы n-го порядка с постоянными коэффициентами. Метод исключения

Основные понятия

Определение 1.Линейной дифференциальной системой n-го порядка с постоянными коэффициентами называется система вида:

(1)

где неизвестные функции; заданные числа, называемые коэффициентами; непрерывные функции на промежутке

Если для всех то система (1) принимает вид:

(2)

и называется линейной однородной дифференциальной системой (ЛОДС).

Если для всех хотя бы одна из функций не равна нулю, то система (1) называется линейной неоднородной дифференциальной системой (ЛНДС).

Определение 2. Порядком системы называется число 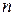неизвестных функций, относительно которых дана система.

Определение 3.Система функций определенных на и удовлетворяющих на всем уравнениям (1), называется решением системы (1).

Определение 4. Задача нахождения удовлетворяющих начальным условиям:

где заданные числа, называется задачей Коши.

Метод исключения

Путем исключения неизвестных функций систему (1) из 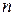линейных уравнений можно привести к дифференциальному уравнению n-го порядка. При этом, если система (1) была линейной неоднородной (или однородной), то и полученное уравнение относительно одной из функций, например будет линейным неоднородным (или однородным). Метод исключения довольно трудоемкий, поэтому им можно пользоваться для или

Примеры с решениями

Пример 1. Решить систему уравнений:

Решение. Это линейная однородная дифференциальная система второго порядка относительно функций Решаем ее методом исключения неизвестных.

Из первого уравнения выразим и подставим во второе уравнение:

Получим линейное однородное дифференциальное уравнение второго порядка. Его характеристическое уравнение имеет вид:

Следовательно, фундаментальную систему решений для этого уравнения составляют функции:

Общее решение запишется в виде:

Для нахождения используем выражение:

Так как то

Тогда

Значит, общим решением данной системы уравнений будут функции

Пример 2. Решить систему уравнений:

Решение. Это линейная неоднородная дифференциальная система относительно 2-х неизвестных функций и Будем решать ее методом исключения.

Из первого уравнения выразим и подставим функцию 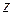во второе уравнение:

(*)

Получили линейное неоднородное дифференциальное уравнение.

1) Решим сначала ЛОДУ:

Его характеристическое уравнение имеет вид:

Фундаментальную систему решений ЛОДУ составляют функции:

Тогда общее решение ЛОДУ запишется в виде:

2) Правая часть ЛНДУ (*): позволяет подобрать его частное решение. Так как то

Подставим вместо в ЛНДУ (*):

Разделим это уравнение на

Следовательно,

3) Запишем общее решение уравнения (*):

4) Найдем используя выражение:

Так как то

Находим

Итак, общим решением системы является система двух функций:

Пример 3. Решить задачу Коши:

Решение. Это линейная неоднородная дифференциальная система относительно неизвестных функций и Будем решать ее методом исключения.

Из первого уравнения выразим и подставим функцию 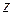во второе уравнение:

(**)

Получим линейное неоднородное дифференциальное уравнение.

1) Решиим сначала ЛОДУ:

Его характеристическое уравнение имеет вид:

Фундаментальную систему решений ЛОДУ составляют функции:

Общее решение ЛОДУ запишется в виде:

2) Правая часть ЛНДУ т.е.

Подставим в уравнение (**) вместо

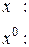
Следовательно,

3) Запишем общее решение уравнения (**):

4) Найдем используя выражение:

Так как то

Тогда:

Итак, общим решением системы будут функции:

5) Найдем такими, чтобы удовлетворяли заданным начальным условиям:

Подставим в полученное общее решение системы:

При полученных значениях запишем частное решение системы:

Примеры

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Ответы