Бесконечно малые и бесконечно большие функции, свойства

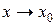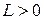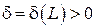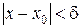Определение. Функция одной переменной называется бесконечно большой при , если для любого сколь угодно большего числа найдется число такое, что для всех , удовлетворяющих условию , выполняется неравенство , т. е. .

Пример. Функция 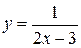есть бесконечно большая функция при .

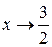Если 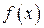стремится к бесконечности при 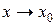и принимает лишь положительные значения, то пишут ; если лишь отрицательные значения, то .

Аналогично можно дать определение для функции 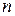– независимых переменных.

Определение.Функция 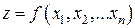называется бесконечно большой при 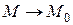, если для любого сколь угодно большого числа 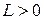найдется такая 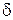–окрестность точки 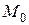, для всех точек которой выполняется неравенство , т.е. .

Пример. Функция двух переменных 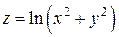в окрестности точки (начало координат) является бесконечно большой функцией, так как 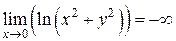(см. рис. 2.2.1).

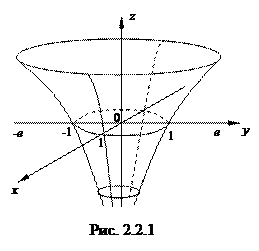
Отметим, что функция 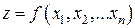может являться бесконечно большой функцией только в окрестности точки 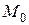; в других частях области определения она может быть ограниченной величиной.

Определение. Функция одной переменной , заданная на всей числовой оси, называется бесконечно большой при 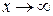, если для любого сколь угодно большого числа 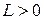найдется такое число , что для всех , удовлетворяющих условию 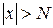, выполняется неравенство 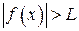, т. е. .

Пример. для есть бесконечно большая функция при 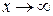, т. е. .

Аналогично, функция 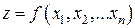, заданная на всех точках 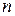– мерного пространства, называется бесконечно большой при 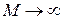, если .

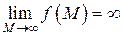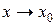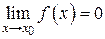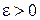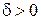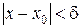Определение. Функция одной переменной называется бесконечно малой при , если , т. е. для любого сколь угодно малого найдется число такое, что для всех , удовлетворяющих условию , выполняется неравенство , т.е. .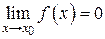

Аналогично определяется бесконечно малая функция при , , , 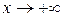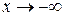: во всех этих случаях .

Примеры.

1. – бесконечно малая при .

2. – бесконечно малая при .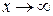

3. – бесконечно малая при , .

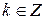Определение. Функция нескольких переменных 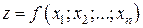называется бесконечно малойпри 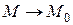, если для любого сколь угодно малого числа 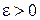найдется такая 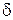– окрестность точки 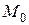, для всех точек которой выполняется неравенство , т.е. .

Пример. Функция двух переменных – бесконечно малая функция в 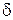– окрестности точки , .

Функция любого числа переменных может быть бесконечно малой функцией только в окрестности предельной точки.

Пример. Функция – бесконечно малая функция в окрестности начала координат пр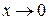и и , а при бесконечном удалении от начала координат по любому направлению при 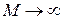она неограниченно возрастает. Следовательно, при 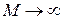она является бесконечно большой функцией.

Бесконечно малые (большие) функции часто называют бесконечно малыми (большими) величинами, их обозначают обычно греческими буквами 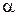, 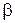и т. д. или .

Свойства бесконечно малой величины и её связь с бесконечно большой величиной сформулируем в виде теорем, и представим доказательства некоторых из них.

Теорема 3. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция, т.е.

если – бесконечно малая функция, где , то – бесконечная функция.

Доказательство: Пусть и 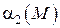две бесконечно малые функции 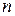независимых переменных при 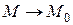. Тогда и .

По определению предела это значит, что для любого 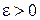, а значит и 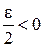найдутся 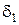– окрестность и 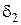– окрестность точки 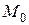, для всех точек которых будут соответственно выполняться неравенства 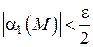и .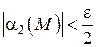

Пусть 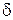– наименьшее из чисел 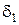и 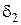, тогда для всех точек из 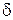– окрестности будут выполняться оба эти неравенства.

Следовательно, имеет место соотношение

.

Это значит, что , т. е. – бесконечно малая величина при 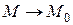. Ч. и т. д.

Доказательство сохраняется, если вместо суммы двух бесконечно малых функций рассматривать их разность, а также в случае любого конечного числа бесконечно малых функций.

Теорема 4. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

Доказательство:

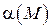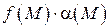Если – бесконечно малая функция, а – ограничена, то – бесконечно малая функция.

Доказательство проведем для функции одного неизвестного.

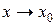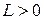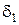Рассмотрим функцию , которая ограничена при , тогда по определению ограниченной функции (см. п. 2.2.4) существует такое , что для всех из – окрестности точки 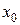выполняется неравенство .

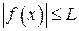Пусть – бесконечно малая функция при 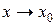, тогда для любого 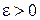, а значит, и найдется такая – окрестность точки 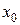, для всех точек которой выполняется неравенство .

Обозначим через 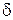наименьшее из чисел 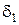и , тогда для всех точек из 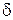– окрестности точки 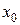выполняются оба неравенства. Следовательно, имеет место соотношение

.

Это значит, что 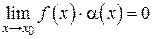, т. е. – бесконечно малая функция.

Следствие 1. Произведение двух бесконечно малых функций есть функция бесконечно малая.

Следствие 2.Произведение числа (постоянной) и бесконечно малой величины есть функция бесконечно малая.

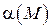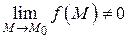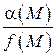Теорема 5. Частное от деления бесконечной малой функции на функцию, имеющую предел отличный от нуля, есть функция бесконечно малая т.е. если – бесконечно малая функция и , то – бесконечно малая величина.

Теорема 6. Если функция – бесконечно малая, то есть бесконечно большая функция и наоборот: если – бесконечно большая функция, то – бесконечно малая.

Доказательство:

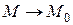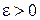Пусть – бесконечно малая функция при , т.е. . Тогда для любого найдется такая 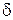– окрестность точки 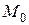, для всех точек которой выполняется неравенство .

Следовательно, 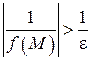, т.е. , где 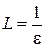. А это означает, что функция – есть бесконечно большая функция. Ч. и т. д.

Аналогично доказывается обратное утверждение.

Замечание. Доказательства теорем 3–6 приводились для случая, когда 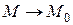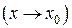, но они справедливы и для случая, когда .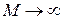

Пример.Показать, что функция при является бесконечно малой.

Решение: функция – бесконечно малая при . функция 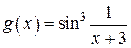, , ограничена.

Таким образом, функция – есть произведение бесконечной малой и ограниченной функции. Значит по теореме 4 это функция бесконечно малая при .

Рассмотрим теорему о связи между функцией, её пределом и бесконечно малой функцией.

Теорема 7. Функция 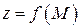имеет предел равный 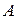тогда и только тогда , когда её можно представить как сумму числа 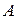и бесконечно малой функции 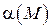, т.е. .

Доказательство:

Докажем прямое утверждение: если 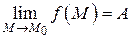, то .

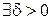
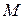Пусть точки из 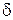– окрестности точки 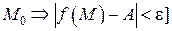, т. е. .

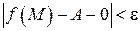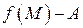Это значит, что , т.е. что функция является бесконечно малой, которую обозначим через 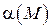, тогда . Отсюда . Ч. и т. д.

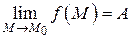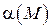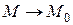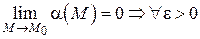
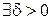
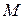Докажем обратное утверждение: если , то . Пусть , где – бесконечно малая функция при , т. е. точки из 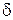– окрестности точки .

По условию , то .

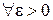
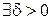
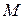Получаем, что точки из 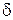– окрестности точки .

А это и означает, что 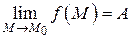. Ч. и т. д.

Теоремы о пределах

Правила, по которым находятся пределы функций, включают теоремы, справедливые для функции любого числа переменных 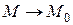при и при .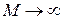

Эти теоремы позволяют находить пределы в тех случаях, когда функции представляют собой результат арифметических действий над другими функциями, пределы которых существуют и заранее известны.

Теорема 1. Предел постоянной равен самой постоянной, т.е. если , то .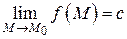

Теорема 2. Предел суммы конечного числа функций в точке равен сумме пределов этих функций в этой точке:

.

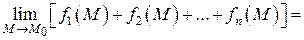
Доказательство:

Приведем доказательство для суммы двух функций. Докажем, что

.

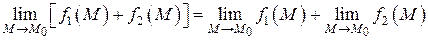Пусть 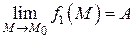и . Тогда по теореме 7 (п. 2.2.1) можно записать 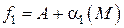и .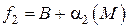

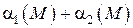Следовательно, , где бесконечно малая функция как сумма бесконечно малых функций. Тогда по теореме 7 (п. 2.2.1) можно записать

,

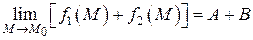т.е.

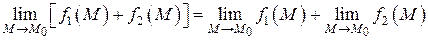. Ч. и т. д.

В случае разности двух функций и суммы любого конечного числа функций доказательство аналогично.

Следствие 1.Функция может иметь только один предел при .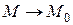

Теорема 3. Предел произведения конечного числа функций в точке 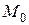равен произведению пределов этих функций в этой точке:

Следствие 2. Постоянный множитель можно выносить за знак предела:

.

Теорема 4. Предел дроби равен пределу числителя, делимому на предел знаменателя, если предел знаменателя не равен нулю:

.

Примеры.

1.Найти .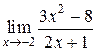

Решение: В данном случае предел функции, стоящей в знаменателе, при 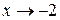отличен от нуля, поэтому можно применить приведенные выше теоремы:

.

Иначе говоря, в данном случае, чтобы найти предел, можно вместо независимой переменной подставить её значение в предельной точке.

2. Найти .

Решение:Функция 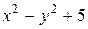, стоящая в знаменателе дроби пр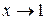и и 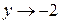стремится к числу , тогда

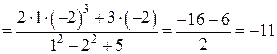
Пример аналогичен предыдущему: вместо независимых переменных необходимо подставить их значения в предельной точке.

3. Найти .

Решение: Предел знаменателя 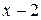при 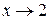равен нулю и теорема 4 не применима. В данном случае воспользуемся свойством бесконечно малой функции (см. п. 2.3.3 теорема 6). Функция – бесконечно малая при 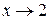, тогда обратная ей дробь – бесконечно большая функция, а значит .

Таким образом, если знаменатель дроби не обращается в ноль, то чтобы найти такой предел, достаточно в выражение функции подставить предельные значения независимых аргументов. Если же знаменатель стремиться к нулю 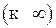, а числитель к некоторому постоянному числу, то при нахождении предела используют свойство бесконечно малой величины (см. п. 2.2.1 теорема 6).

В случае неопределенных выражений, характеризуемых условно символами: (будем называть их неопределенностями), которые возникают при отыскании предела выражени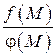й: ; ; или предел может существовать или не существовать. В пределах такого типа, требуются дополнительные преобразования или специальные исследования. Рассмотрим некоторые из них.

I. Требуется найти предел дробно-рационального выражения вида (отношение двух многочленов) при , тогда в пределе будет иметь место неопределенность . Чтобы раскрыть её, необходимо числитель и знаменатель дроби разделить на переменную в наибольшей степени.

Пример. .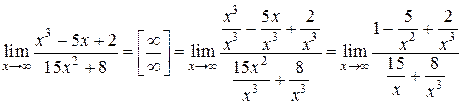

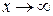Предел числителя равен , а знаменатель при сумма бесконечно малых величин, т.е. величина бесконечно малая, поэтому вся дробь – есть бесконечно большая величина, т.е. .

Пользуясь рассмотренным выше способом можно вывести правило раскрытия неопределенности в пределе отношения двух многочленов

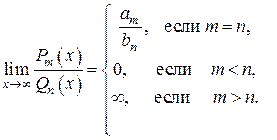
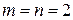Пример. , так как и , .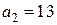

II.Пусть требуется найти предел дроби, числитель и знаменатель которой стремятся к нулю при 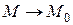, тогда в пределе будет иметь место неопределенность .

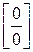а) Если числитель и знаменатель – многочлены, то чтобы раскрыть данную неопределенность, необходимо числитель и знаменатель разложить на множители и сократить дробь.

В некоторых случаях удобнее разделить числитель и знаменатель на критический множитель (для функции одной переменной), или воспользоваться определением предела.

Примеры.

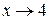1. (при сокращении на учитывается, что , но ).

2.

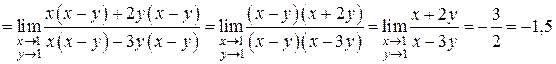
3. 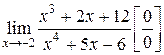. Разделим числитель и знаменатель на критический множитель :

Тогда .

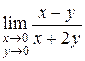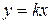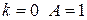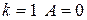4. . Будем приближаться к началу координат по прямым , тогда . Имеем при ; при ; при и т.д. Отсюда следует, что предел этой функции не существует.

b) Если дробь является иррациональным выражением, в некоторых случаях, чтобы раскрыть данную неопределенность необходимо числитель и знаменатель дроби умножить на выражение, сопряженное иррациональному или применить подстановку.

Примеры.

1. 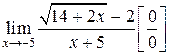. Умножим числитель и знаменатель на выражение – сопряженное числителю .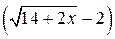

,

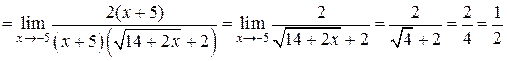таким образом .

2. .

Выполним подстановку при

.

Таким образом, .