Определение. Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид , где - положительные числа

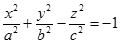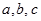Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид , где - положительные числа.

Исследуем форму двуполостного гиперболоида. Так же, как эллипсоид и однополостный гиперболоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.

Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 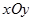. На этой плоскости 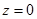, поэтому .

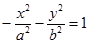Координаты ни одной точки плоскости 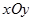не могут удовлетворять данному уравнению. Следовательно, двуполостный гиперболоид не пересекает эту плоскость. Найдем линию пересечения с плоскостью 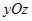. На этой плоскости 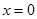, поэтому .

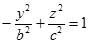Это уравнение гиперболы на плоскости 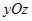, где действительная полуось равна 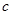, а мнимая полуось равна 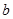. Построим эту гиперболу (рис. 11).

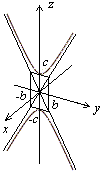
Рис. 11.Сечения двуполостного гиперболоида плоскостью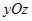

Сечение плоскостью 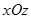также является гиперболой, с уравнением 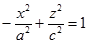. Построим гиперболу, но чтобы не перегружать чертеж дополнительными линиями, не будем изображать ее асимптоты и уберем асимптоты в сечении плоскостью 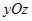(рис.12).

Найдем линии пересечения поверхности с плоскостями 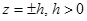. Уравнения этих линий

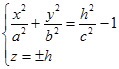
Очевидно, что ни одна точка не может удовлетворять этим уравнениям, если 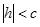. Ес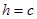ли или 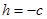, то плоскость имеет с исследуемой поверхностью только одну точку 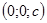или 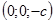. Эти точки называются вершинами гиперболоида.

Пусть 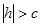. Первое уравнение преобразуем к виду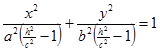

Введём обозначения 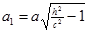, , 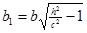тогда уравнение примет вид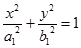

Данное уравнение является уравнением эллипса, подобного эллипсу в плоскости 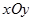, с коэффициентом подобия 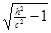и полуосям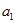и и 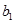. Нарисуем полученные сечения (рис. 12).

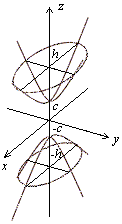
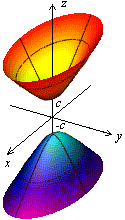
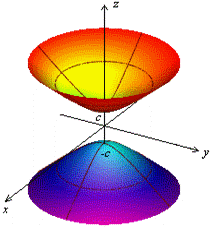Рис. 12 Изображение двуполостного. Рис. 13. Двуполостный гиперболоид. Рис. 14 Двуполостный гиперболоид

гиперболоида с помощью сечений вращения

Если в уравнении 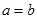, то сечения гиперболоида плоскостями, параллельными плоскости 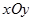, являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения и может быть получена вращением гиперболы, лежащей в плоскости 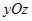, вокруг оси 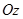(рис.14).

Конус