Определение линейного оператора
IV. Пространства операторов
Определение линейного оператора
Пусть X и Y –нормированные пространства, оба вещественные или оба комплексные или линейные топологические пространства.
Определение 1. Линейным оператором, действующим из пространства X в пространство Y называется отображение 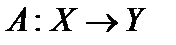 или
или 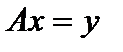 или
или 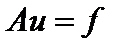 (если
(если 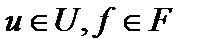 ,где
,где 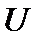 и
и 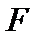
 пространства функций), удовлетворяющее условию
пространства функций), удовлетворяющее условию 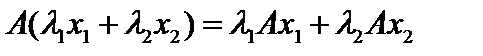 , где
, где 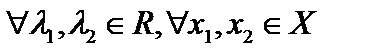 .
.
Пример 1. Пусть 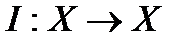 по правилу
по правилу 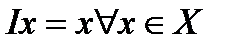 , то есть оператор I переводит каждый вектор пространства X в себя. Ясно, что
, то есть оператор I переводит каждый вектор пространства X в себя. Ясно, что 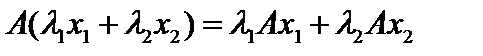 . Это единичный оператор. Соответственно, нулевой оператор
. Это единичный оператор. Соответственно, нулевой оператор 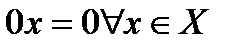 переводит каждый вектор пространства
переводит каждый вектор пространства 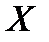 в нулевой вектор пространства
в нулевой вектор пространства 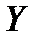 .
.
Комментарий. Единичный оператор иногда обозначают буквой 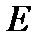 . Это те, кто считает, что слово единица пишется через “E”. Символ 0 теперь может означать либо число нуль, либо нулевой вектор пространства
. Это те, кто считает, что слово единица пишется через “E”. Символ 0 теперь может означать либо число нуль, либо нулевой вектор пространства 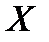 , либо нулевой вектор пространства
, либо нулевой вектор пространства 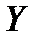 , либо нулевой оператор, действующий из пространства
, либо нулевой оператор, действующий из пространства 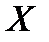 в пространство
в пространство 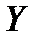 .
.
Пример 2. Пусть 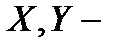 конечномерные эвклидовы пространства,
конечномерные эвклидовы пространства, 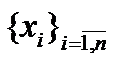 базис в пространстве
базис в пространстве 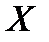 а
а 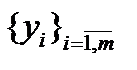 базис в пространстве
базис в пространстве 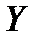 . Тогда
. Тогда 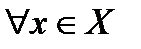 верно, что
верно, что 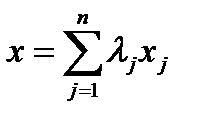 . Оператор A линеен, то есть
. Оператор A линеен, то есть 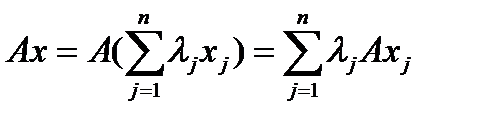 . Но каждый из векторов
. Но каждый из векторов 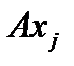 лежит в пространстве
лежит в пространстве 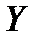 и поэтому может быть разложен по базису
и поэтому может быть разложен по базису 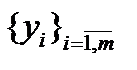 :
: 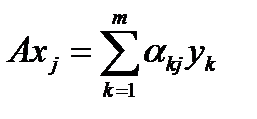 . Тогда
. Тогда 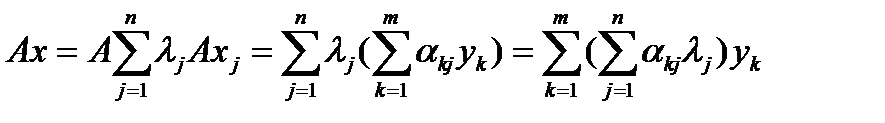 . Совокупность чисел
. Совокупность чисел 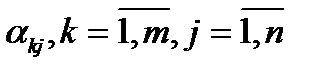 называется матрицей оператора A. Совокупность чисел
называется матрицей оператора A. Совокупность чисел 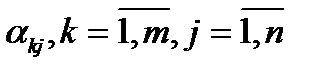 называется матрицей оператора A. То есть каждому оператору
называется матрицей оператора A. То есть каждому оператору 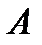 соответствует некоторая матрица
соответствует некоторая матрица 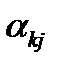 и наоборот, каждой матрице
и наоборот, каждой матрице 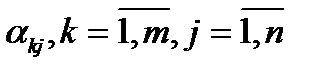 соответствует некоторый линейный оператор A. Поскольку векторы
соответствует некоторый линейный оператор A. Поскольку векторы 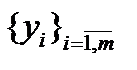 линейно независимы, то коэффициенты при векторе
линейно независимы, то коэффициенты при векторе 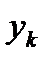 в левой и правой частях последней формулы должны совпадать, то есть
в левой и правой частях последней формулы должны совпадать, то есть 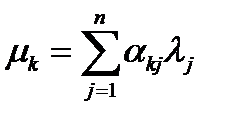 , или
, или 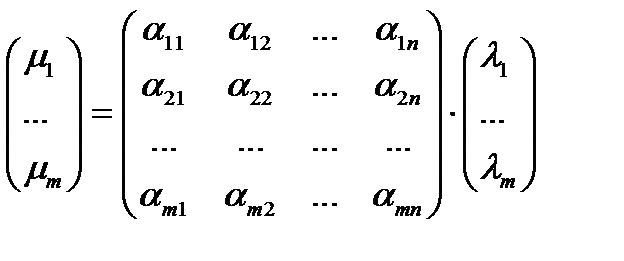 .
.
Определение 2. Оператор А ограничен,если для любых xÎ X, справедлива оценка 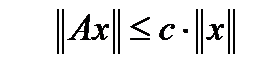 , где с – постоянная. Точная нижняя грань всех таких констант с на называется нормой оператора А и обозначается
, где с – постоянная. Точная нижняя грань всех таких констант с на называется нормой оператора А и обозначается 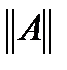 .
.
Комментарий. По определению, 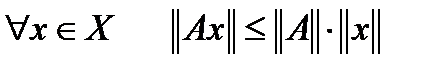 , то есть норма
, то есть норма 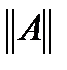 во первых, одна из верхних граней, а во вторых
во первых, одна из верхних граней, а во вторых 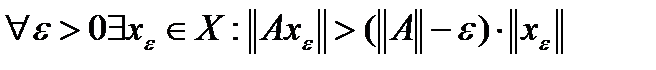 , что означает несдвигаемость верхней грани.
, что означает несдвигаемость верхней грани.
Теорема 1. 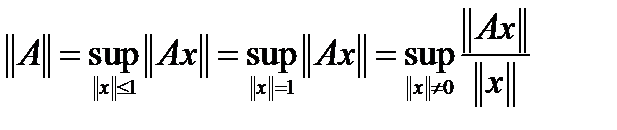
 Обозначим
Обозначим 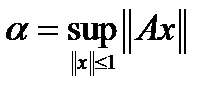 ,
, 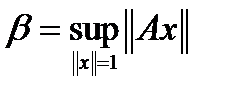 ,
, 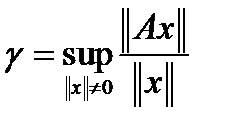 . Покажем, что
. Покажем, что 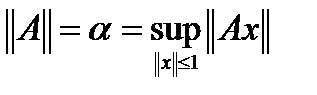 . Так как
. Так как 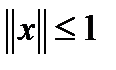 , то
, то 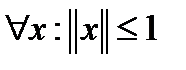
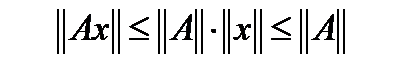 . Тогда
. Тогда 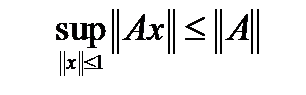 . С другой стороны из несдвигаемости верхней грани следует, что
. С другой стороны из несдвигаемости верхней грани следует, что 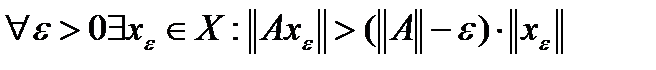 . Рассмотрим элемент
. Рассмотрим элемент 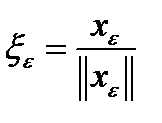 . Тогда для него
. Тогда для него 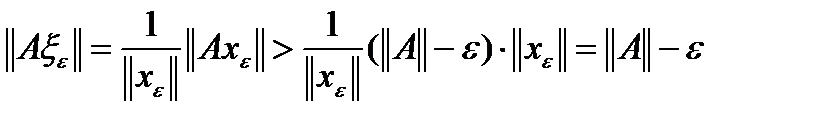 . Но норма
. Но норма 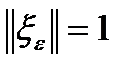 , поэтому
, поэтому 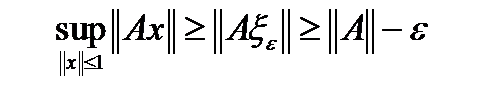 . В силу произвольности
. В силу произвольности 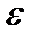 , сразу получаем
, сразу получаем 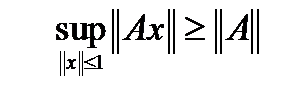 . Таким образом
. Таким образом 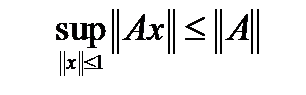 . Но одновременно
. Но одновременно 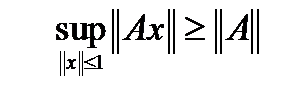 , то есть
, то есть 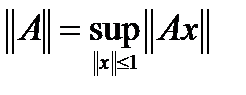 .
.
Покажем теперь, что выполняются и остальные равенства. Для этого докажем, что 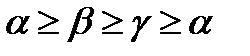 . Первое неравенство
. Первое неравенство 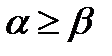 очевидно, поскольку в обеих его частях супремум берется от одной и той же величины
очевидно, поскольку в обеих его частях супремум берется от одной и той же величины 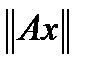 . Второе неравенство
. Второе неравенство 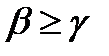 следует из того, что для любого
следует из того, что для любого 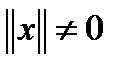
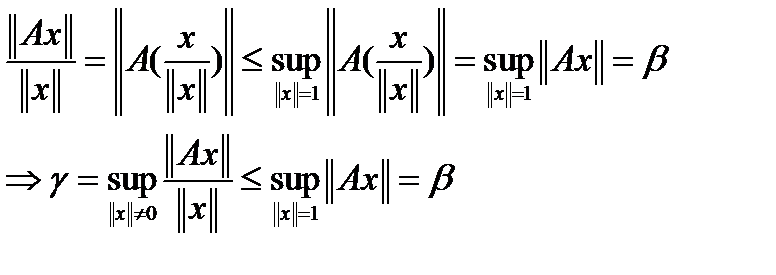 .
.
Третье неравенство 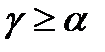 следует из того, что для любого
следует из того, что для любого 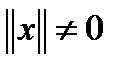 и
и 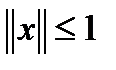 имеем
имеем 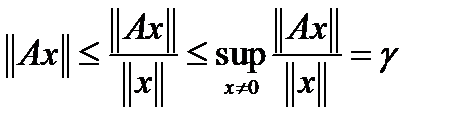 .
. 
Комментарий. Для числовых функций линейная функция всегда ограничена. В конечномерных пространствах любой линейный оператор является ограниченным. Для линейного оператора в бесконечномерных пространствах это, вообще говоря, не так.
Пример 3. Оператор дифференцирования. Рассмотрим операторное уравнение 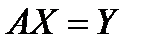 в пространствах
в пространствах 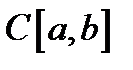 . Пусть оператор дифференцирования
. Пусть оператор дифференцирования 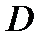 действует из
действует из 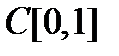 в
в 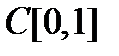 , то естьоператор
, то естьоператор 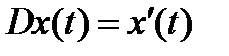 . Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную. В пространстве
. Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную. В пространстве 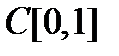 норма
норма 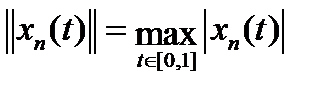 .Достаточно указать один элемент пространства, для которого ограниченность не имеет места. Возьмем из
.Достаточно указать один элемент пространства, для которого ограниченность не имеет места. Возьмем из 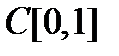 последовательность хn(t) = tn. Она ограничена в
последовательность хn(t) = tn. Она ограничена в 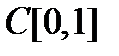 :
: 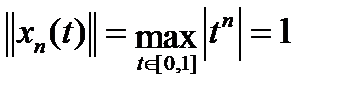 . Рассмотрим
. Рассмотрим 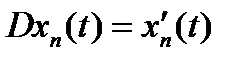 = =
= = 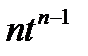 .Тогда норма
.Тогда норма 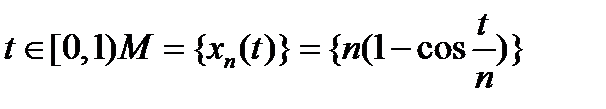 . Таким образом, оператор
. Таким образом, оператор 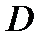 переводит ограниченное множество в неограниченное, то есть этот оператор не является ограниченным. Такая же ситуация с последовательностью
переводит ограниченное множество в неограниченное, то есть этот оператор не является ограниченным. Такая же ситуация с последовательностью 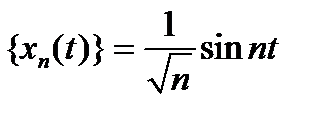 . В
. В 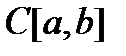 норма
норма 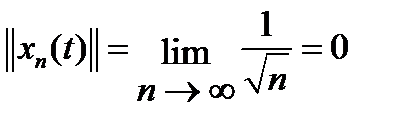 , а
, а 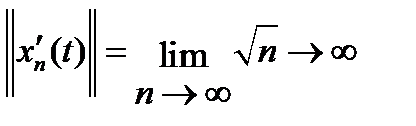 . Тогда
. Тогда 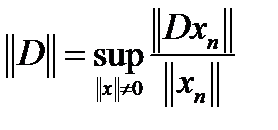 при
при 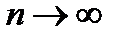 тоже стремится к бесконечности, то есть оператор дифференцирования А неограничен, то есть не является непрерывным. Но если в пространстве исходных данных Х выбрать более сильную норму, то ситуация изменится. Рассмотрим пространство Х как пространство
тоже стремится к бесконечности, то есть оператор дифференцирования А неограничен, то есть не является непрерывным. Но если в пространстве исходных данных Х выбрать более сильную норму, то ситуация изменится. Рассмотрим пространство Х как пространство 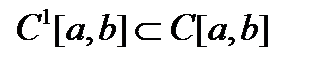 а пространство У как пространство С[a,b]. Тогда
а пространство У как пространство С[a,b]. Тогда 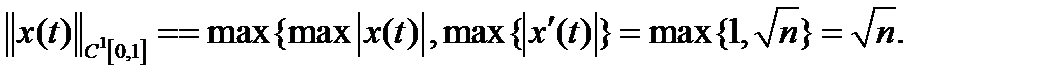 Теперь
Теперь 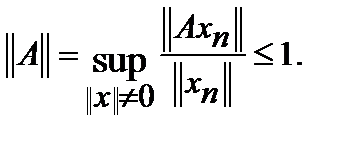
Пример. Линейный функционал в 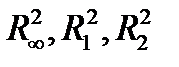
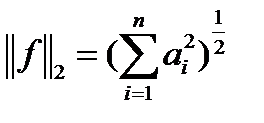 в точках (1,2) и (3,4) равен 5 и 6 соответственно. Найти его значение в точке (7,8) и норму.
в точках (1,2) и (3,4) равен 5 и 6 соответственно. Найти его значение в точке (7,8) и норму.
Пример. Значение линейного функционала в 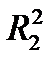 в точке (1,1) равно
в точке (1,1) равно 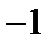 , а его норма равна
, а его норма равна 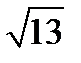 . Найти его значение в точке (7,8).
. Найти его значение в точке (7,8).  Линейный функционал, заданный на плоскости, имеет вид
Линейный функционал, заданный на плоскости, имеет вид 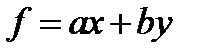 , то есть это плоскость, проходящая через начало координат. Его норма – это максимальное значение этой функции на единичном шаре в
, то есть это плоскость, проходящая через начало координат. Его норма – это максимальное значение этой функции на единичном шаре в 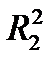 . Таким образом, имеем симметрическую СЛАУ
. Таким образом, имеем симметрическую СЛАУ 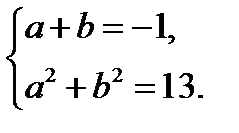

Пример. Значение линейного функционала в 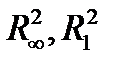 в точке (1,1) равно
в точке (1,1) равно 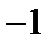 , а его норма равна
, а его норма равна 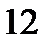 . Найти его значение в точке (7,8).
. Найти его значение в точке (7,8).
Комментарий. Из геометрического смысла понятия нормы видно, что общий вид линейного функционала в пространствах 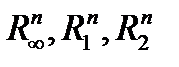 задаётся формулой
задаётся формулой 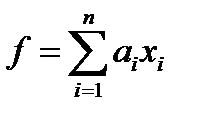 , где
, где 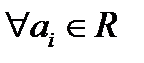 . Нормы же их определяются выражениями
. Нормы же их определяются выражениями 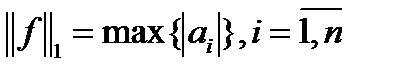
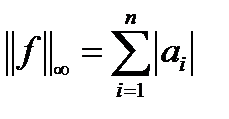
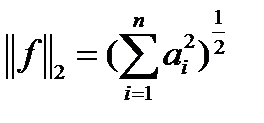 .
.
Пример.Рассмотрим преобразование двумерного пространства 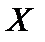 в двумерное пространство
в двумерное пространство 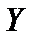 оператором
оператором 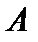 , причём матрица линейного оператора
, причём матрица линейного оператора 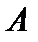 невырождена и имеет вид
невырождена и имеет вид 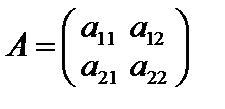 .
.
1.Рассмотримпреобразование 
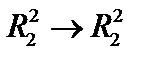 , где точки
, где точки 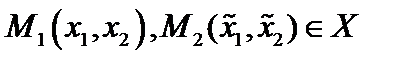 , а точки
, а точки 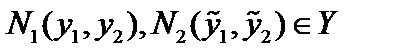 . Тогда
. Тогда 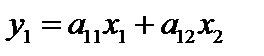 , а
, а 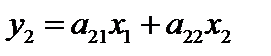 . Обозначим
. Обозначим 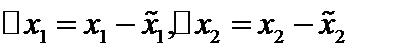 . Тогда
. Тогда 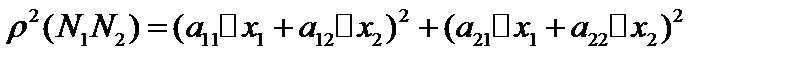 . Запишем это как скалярное произведение и воспользуемся неравенством Буняковского
. Запишем это как скалярное произведение и воспользуемся неравенством Буняковского 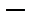 Коши.
Коши.
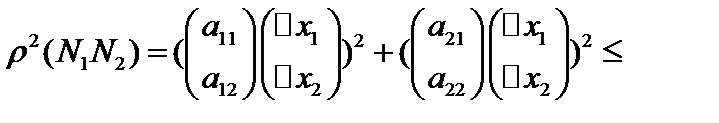
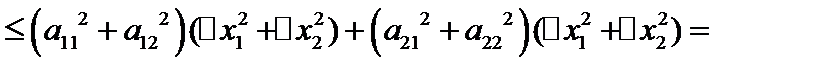
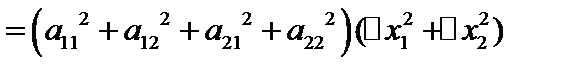 . Тогда
. Тогда
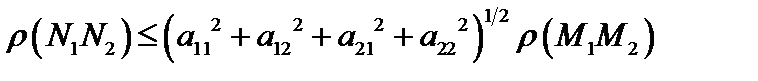 , то есть
, то есть 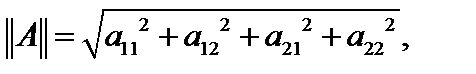 а норма
а норма 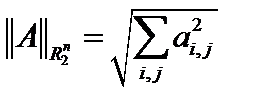 называется эвклидовой.
называется эвклидовой.
2. Рассмотримпреобразование 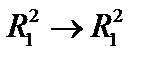 .
.
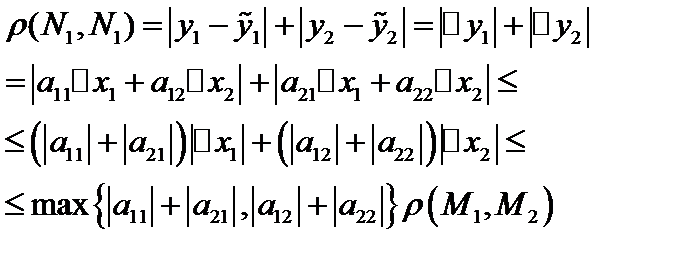
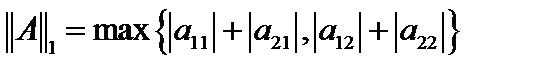 . Такая норма называется столбиковой.
. Такая норма называется столбиковой.
3. Рассмотримпреобразование 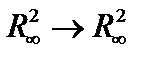 .
.
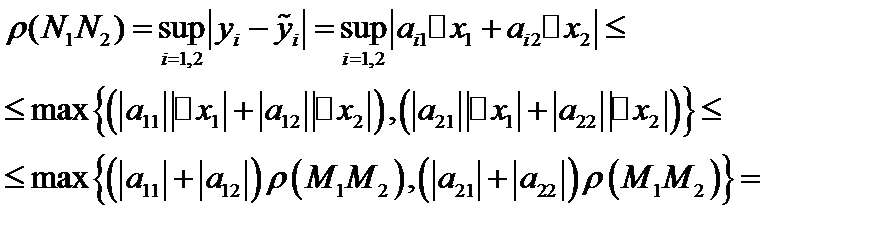
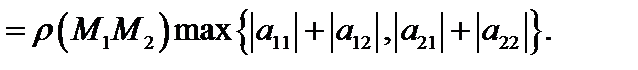
Тогда 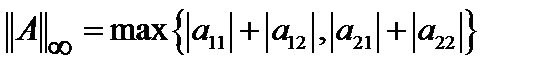
Такая норма называется строчной.
Непрерывность
Пусть X и Y – нормированные пространства и А: X → Y, где А – линейный оператор, всюду заданный в X (т.е. 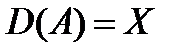 ).
).
Определение 1.Линейный оператор А, заданный всюду в банаховом пространстве X и со значениями в банаховом пространстве Y называется непрерывным в точке 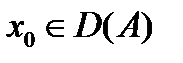 , если
, если 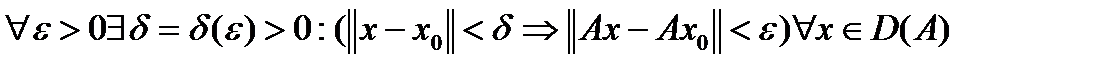 . Эквивалентное определение непрерывности оператора в точке:
. Эквивалентное определение непрерывности оператора в точке:
Определение 2.Линейный оператор А, заданный всюду в банаховом пространстве X и со значениями в банаховом пространстве Y называется непрерывным в точке 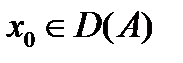 , если для любой последовательности xn, n=1, 2, …,
, если для любой последовательности xn, n=1, 2, …, 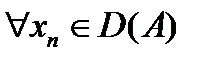 ,xn→x0, последовательность Axn сходится к Ax0.
,xn→x0, последовательность Axn сходится к Ax0.
Определение 3.Оператор A называется непрерывным на D(A), если он непрерывен в каждой точке.
Теорема 1. Линейный оператор А, заданный всюду в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен тогда и только тогда, когда он непрерывен в нуле.
Необходимость.  Ясно, что если оператор А непрерывен в каждой точке, то он непрерывен в нуле.
Ясно, что если оператор А непрерывен в каждой точке, то он непрерывен в нуле. 
Достаточность.  Пусть оператор A непрерывен в нуле и
Пусть оператор A непрерывен в нуле и 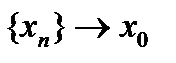 . Тогда
. Тогда 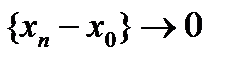 , а так как оператор A непрерывен в нуле и линеен, то
, а так как оператор A непрерывен в нуле и линеен, то 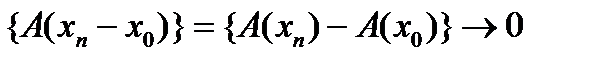 .
. 
Определение 4. Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.
Теорема 2. Пусть А: X → Y, А – линейный оператор, X, Y – банаховы пространства. Для того чтобы линейный оператор А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.
Необходимость.  Пусть оператор А ограничен. Покажем, что он непрерывен. Достаточно доказать непрерывность А в нуле. Рассмотрим любую последовательность
Пусть оператор А ограничен. Покажем, что он непрерывен. Достаточно доказать непрерывность А в нуле. Рассмотрим любую последовательность 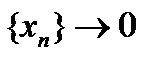 , то есть
, то есть 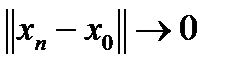 . Тогда
. Тогда 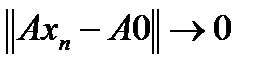 , то есть
, то есть 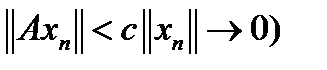 , так как оператор А ограничен, а
, так как оператор А ограничен, а 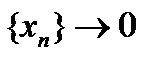 , то есть
, то есть 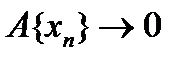 , то есть оператор А непрерывен в нуле.
, то есть оператор А непрерывен в нуле. 
Достаточность. 
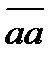 . Допустим, что оператор А не ограничен. Это значит, что числу 1 найдется хотя бы один соответственный вектор x1 такой, что ||A x1|| > 1|| x1||. Числу 2 найдется вектор x2, что ||A x2|| > 2|| x2|| и т.д. Числу n найдется вектор xn, что ||A xn|| > n|| xn||. Теперь рассмотрим последовательность векторов yn =
. Допустим, что оператор А не ограничен. Это значит, что числу 1 найдется хотя бы один соответственный вектор x1 такой, что ||A x1|| > 1|| x1||. Числу 2 найдется вектор x2, что ||A x2|| > 2|| x2|| и т.д. Числу n найдется вектор xn, что ||A xn|| > n|| xn||. Теперь рассмотрим последовательность векторов yn = 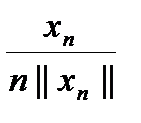 , где ||yn|| =
, где ||yn|| = 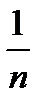 . Следовательно, последовательность yn
. Следовательно, последовательность yn 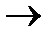 0 при n
0 при n 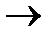
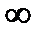 . Так как оператор А непрерывен в нуле, то Аyn
. Так как оператор А непрерывен в нуле, то Аyn 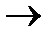 0, однако ||Аyn || = ||A
0, однако ||Аyn || = ||A 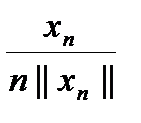 || =
|| = 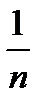 ||Axn||
||Axn|| 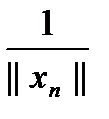 > n|| xn||
> n|| xn|| 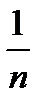
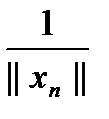 = 1, получаем противоречие с тем, что Аyn
= 1, получаем противоречие с тем, что Аyn 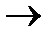 0, то есть А – ограничен.
0, то есть А – ограничен. 
Комментарий. Для линейных операторов понятия ограниченности и непрерывности оператора эквивалентны. Непрерывные линейные операторы будем обозначать аббревиатурой НЛО. Из примера 2 предыдущего пункта следует, что линейный оператор дифференцирования не является непрерывным.
Пример 1. Рассмотрим оператор Фредгольма в пространстве 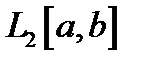 , сопоставляющий функции
, сопоставляющий функции 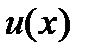 новую функцию
новую функцию 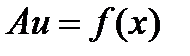 , определенную с помощью формулы
, определенную с помощью формулы 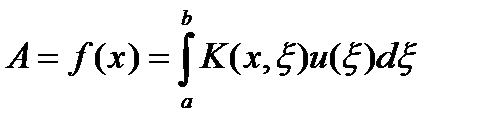 , где
, где 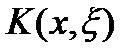 - некоторая фиксированная непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро
- некоторая фиксированная непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро 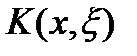 непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном пространстве функций.
непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном пространстве функций.
1. Покажем, что оператор Фредгольма ограничен, а, следовательно, непрерывен при действии 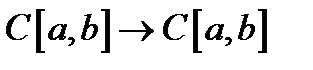 . Полагаем ядро
. Полагаем ядро 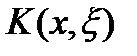 непрерывным в квадрате
непрерывным в квадрате 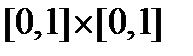 , то есть ограниченным, то есть
, то есть ограниченным, то есть 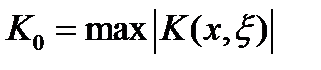 , а норма
, а норма 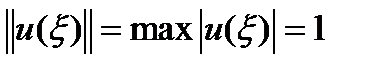 .Тогда
.Тогда 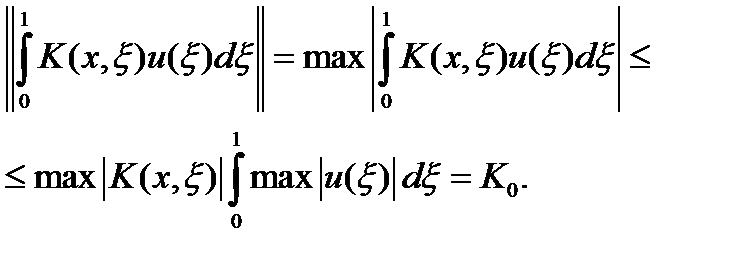 .
.
2. Покажем, что оператор Фредгольма ограничен и, следовательно, непрерывен в пространстве 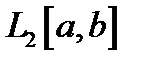 . По неравенству Коши-Буняковского для каждого фиксированного
. По неравенству Коши-Буняковского для каждого фиксированного 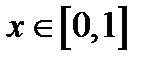 , полагая, что
, полагая, что 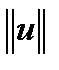
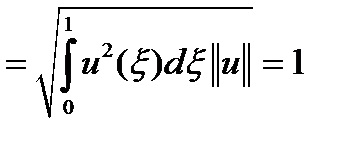 , можно записать
, можно записать 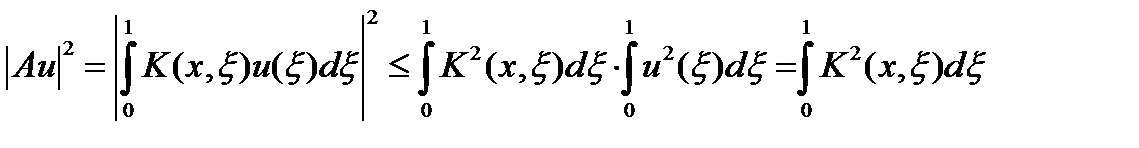 Интегрируем по
Интегрируем по 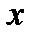 :
: 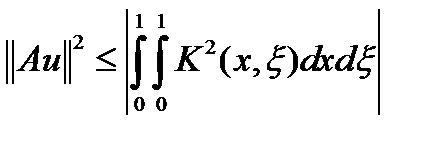 . Правая часть неравенства не зависит от
. Правая часть неравенства не зависит от 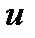 и ограничена, поэтому
и ограничена, поэтому 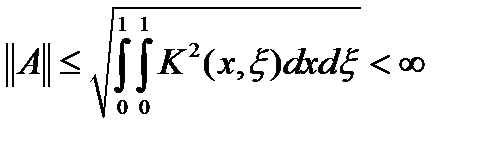 .
.
Наиболее общее определение непрерывности было дано на языке топологии и это позволяет доказать следующее утверждение:
Теорема 3. (Принцип открытости отображений Банаха): Пусть 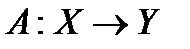
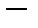 линейный непрерывный оператор,
линейный непрерывный оператор, 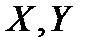
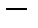 банаховы пространства. Тогда образ любого открытого множества в пространстве
банаховы пространства. Тогда образ любого открытого множества в пространстве 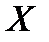 есть открытое множество в пространстве
есть открытое множество в пространстве 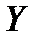 .
.
Лемма 1. Пусть 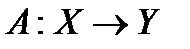
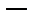 линейный непрерывный оператор,
линейный непрерывный оператор, 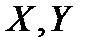
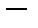 банаховы пространства. Тогда для любой окрестности нуля
банаховы пространства. Тогда для любой окрестности нуля 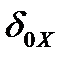 в пространстве
в пространстве 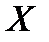 , замыкание образа этой окрестности
, замыкание образа этой окрестности 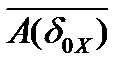 содержит в себе некоторую окрестность нуля
содержит в себе некоторую окрестность нуля 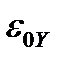 в пространстве
в пространстве 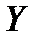 , то есть
, то есть 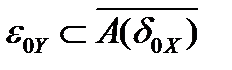 .
.
 Открытая окрестность нуля
Открытая окрестность нуля 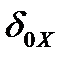 в пространстве
в пространстве 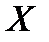 содержит в себе некий открытый шар
содержит в себе некий открытый шар 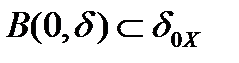 . Зададим
. Зададим 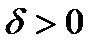 и рассмотрим последовательность
и рассмотрим последовательность 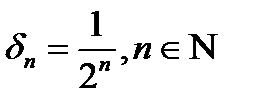 . Тогда для любого фиксированного
. Тогда для любого фиксированного 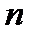
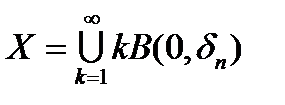 . То есть любой вектор
. То есть любой вектор 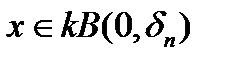 , где
, где 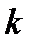 - наименьшее из целых чисел, больших
- наименьшее из целых чисел, больших 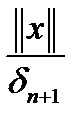 . Оператор А сюръективен, то есть
. Оператор А сюръективен, то есть 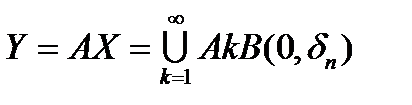 . По условию
. По условию 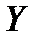 - Банахово пространство, которое по теореме Бэра о категориях есть множество II категории, то есть его нельзя представить в виде объединения счётного числа нигде не плотных множеств, то есть существует номер
- Банахово пространство, которое по теореме Бэра о категориях есть множество II категории, то есть его нельзя представить в виде объединения счётного числа нигде не плотных множеств, то есть существует номер 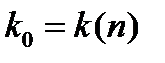 и открытое множество
и открытое множество 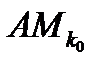 , такие, что найдётся шар
, такие, что найдётся шар 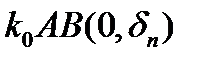 , который будет плотным в открытом множестве
, который будет плотным в открытом множестве 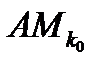 . Другими словами,
. Другими словами, 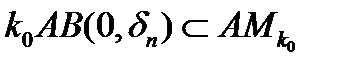 , но множество
, но множество 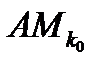 будет содержаться в замыкании шара
будет содержаться в замыкании шара 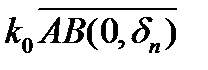 , или шар
, или шар 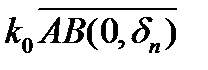 будет содержать в себе некоторое открытое множество
будет содержать в себе некоторое открытое множество 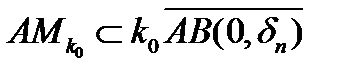 . Можно сказать, что замыкание шара
. Можно сказать, что замыкание шара 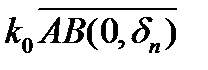 имеет непустую открытую внутренность
имеет непустую открытую внутренность 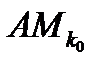 . Так как оператор А непрерывен, то соответствующее множество в пространстве
. Так как оператор А непрерывен, то соответствующее множество в пространстве 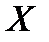 , множество
, множество 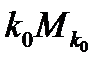 тоже будет открыто, как и множество
тоже будет открыто, как и множество 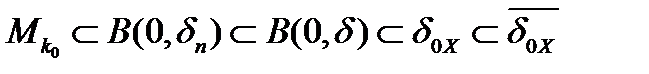 . С другой стороны, множество
. С другой стороны, множество 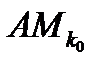 и есть окрестность нуля в пространстве
и есть окрестность нуля в пространстве 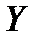 , то есть можно считать, что
, то есть можно считать, что 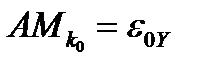 . Тогда сразу
. Тогда сразу 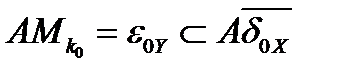 .
. 
Лемма 2. Пусть 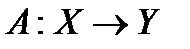 - линейный непрерывный оператор,
- линейный непрерывный оператор, 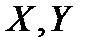 - банаховы пространства. Тогда для любой окрестности нуля
- банаховы пространства. Тогда для любой окрестности нуля 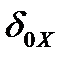 в пространстве
в пространстве 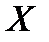 , образ этой окрестности
, образ этой окрестности 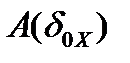 содержит в себе некоторую окрестность нуля
содержит в себе некоторую окрестность нуля 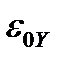 в пространстве
в пространстве 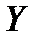 , то есть
, то есть 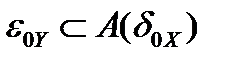 .
.
 . Открытая окрестность нуля
. Открытая окрестность нуля 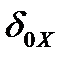 в пространстве
в пространстве 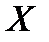 содержит в себе некий открытый шар
содержит в себе некий открытый шар 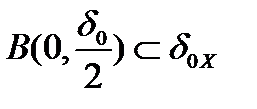 . Возьмём произвольную последовательность
. Возьмём произвольную последовательность 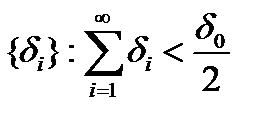 и обозначим
и обозначим 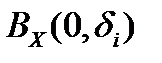 открытые шары радиусов
открытые шары радиусов 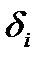 , а
, а 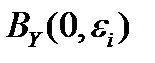 - открытые шары радиусов
- открытые шары радиусов 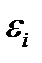 . В силуЛеммы 1
. В силуЛеммы 1 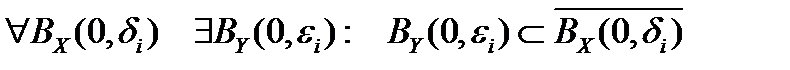 , причём последовательность
, причём последовательность 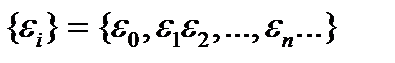 монотонно убывает. Пусть
монотонно убывает. Пусть 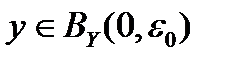 . Так как
. Так как 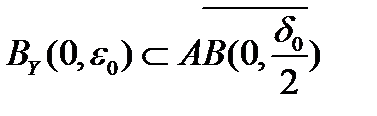 , то найдётся точка
, то найдётся точка 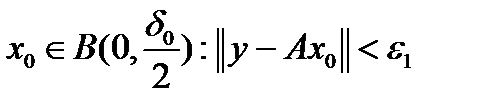 . Так как
. Так как 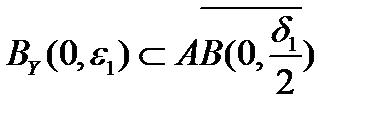 , то найдётся точка
, то найдётся точка 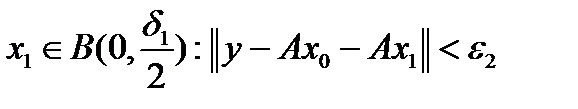 . И так далее. Таким образом
. И так далее. Таким образом 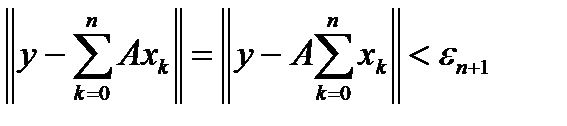 . Пусть
. Пусть 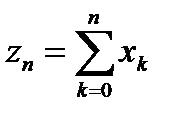 . Оценим норму
. Оценим норму 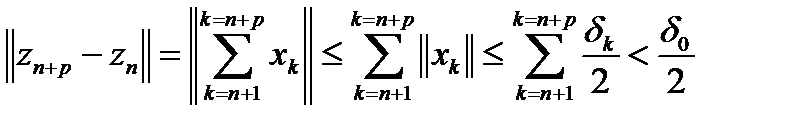 , то есть последовательность
, то есть последовательность 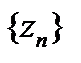 фундаментальна в пространстве
фундаментальна в пространстве 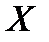 . Так как пространство
. Так как пространство 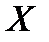 полное, то она сходится, то есть существует элемент
полное, то она сходится, то есть существует элемент 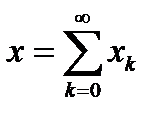 , такой, что
, такой, что 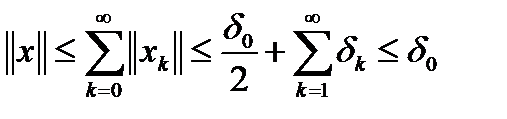 . Тогда, в силу соотношения
. Тогда, в силу соотношения 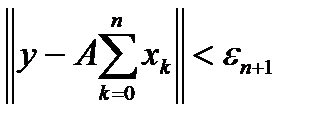 имеем
имеем 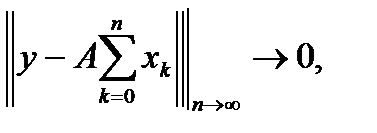 и
и 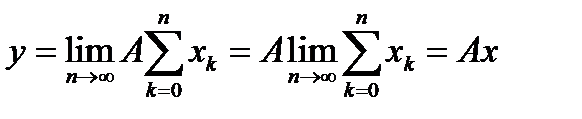 . Таким образом, мы фактически показали, что образ
. Таким образом, мы фактически показали, что образ 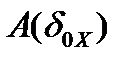 любой окрестности нуля
любой окрестности нуля 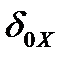 в пространстве
в пространстве 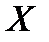 , содержит в себе некоторую окрестность нуля
, содержит в себе некоторую окрестность нуля 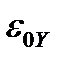 в пространстве
в пространстве 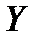 , то есть
, то есть 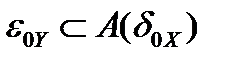 .
. 
Теперь легко доказатьпринцип открытости отображений Банаха.
 Нулевой элемент пространства
Нулевой элемент пространства 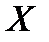 - такой же элемент пространства
- такой же элемент пространства 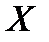 , как и все остальные. То есть если
, как и все остальные. То есть если 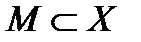 - произвольное открытое множество в пространстве
- произвольное открытое множество в пространстве 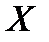 , то
, то 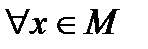
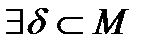 . Обозначим через
. Обозначим через 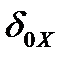 такую окрестность нуля, что её сдвиг на
такую окрестность нуля, что её сдвиг на 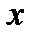 , то есть
, то есть 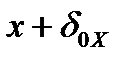 окажется внутри
окажется внутри 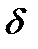 :
: 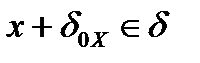 . Так как
. Так как 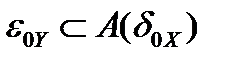 , то
, то 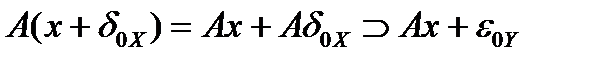 . В силу произвольности
. В силу произвольности 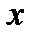 теорема доказана.
теорема доказана.  .
.
Комментарий. У непрерывного оператора можно посчитать конечное значение норм входного и выходного элементов, максимальное значение этого отношения на всем множестве определения дает согласованную норму самого этого оператора. Грубо говоря, это максимальный "коэффициент усиления" преобразования. Поскольку норма это число, то множество операторов должно быть замкнуто относительно обычных алгебраических операций. Но будет ли оно пространством, то есть можно ли на этом множестве определить операцию предельного перехода и если да, то будет ли это пространство полным? ( Под пространством в функциональном анализе понимают не просто множество с заданным, кроме отношения равенства, каким 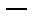 либо отношением. Это отношение должно допускать операцию предельного перехода.)
либо отношением. Это отношение должно допускать операцию предельного перехода.)
Обозначим множество всех непрерывных линейных операторов, действующих из пространства 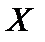 в пространство
в пространство 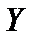 , через
, через 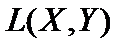 . Очевидно,
. Очевидно, 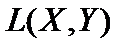 линейное пространство.
линейное пространство.
Теорема 4. Пространство 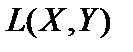 есть нормированное пространство с нормой
есть нормированное пространство с нормой 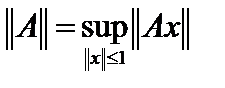 .
.
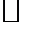 . Достаточно проверить для
. Достаточно проверить для 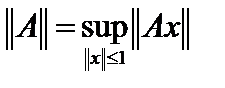 аксиомы нормы.
аксиомы нормы. 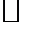
Определение 5. Последовательность линейных непрерывных операторов 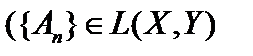 сходится равномерно к оператору
сходится равномерно к оператору 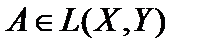 , если
, если 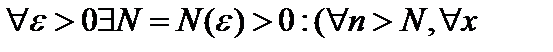 из шара
из шара 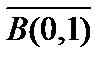 верно, что
верно, что 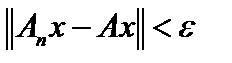 .
.
Это обозначают как 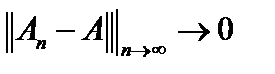 .
.
Теорема 5. Если X есть нормированное пространство, a Y банахово, то пространство 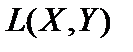 банахово в смысле равномерной сходимости.
банахово в смысле равномерной сходимости.
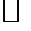 . Надо показать, что существует непрерывный линейный оператор
. Надо показать, что существует непрерывный линейный оператор 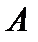 , который является пределом равномерно сходящейся последовательности операторов
, который является пределом равномерно сходящейся последовательности операторов 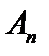 .
.
1. Покажем существование непрерывного оператора 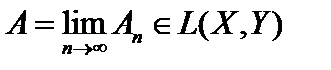 . Рассмотрим произвольную фундаментальную последовательность
. Рассмотрим произвольную фундаментальную последовательность 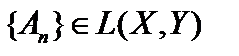 . Для любого элемента
. Для любого элемента 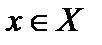 последовательность
последовательность 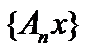 фундаментальна, так как
фундаментальна, так как 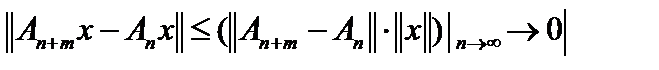 и
и 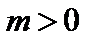 . Пространство Y банахово, то есть найдётся
. Пространство Y банахово, то есть найдётся 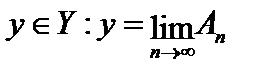 . Таким образом, каждому элементу
. Таким образом, каждому элементу 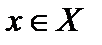 мы поставили в соответствие единственный элемент
мы поставили в соответствие единственный элемент 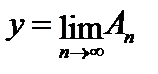 ,
, 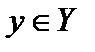 . Оператор
. Оператор 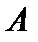 линеен, так как линейны операторы
линеен, так как линейны операторы 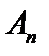 .
.
2. Покажем, что оператор 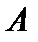 ,являющийся пределом для последовательности операторов
,являющийся пределом для последовательности операторов 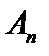 , непрерывен. В самом деле, так как последовательность
, непрерывен. В самом деле, так как последовательность 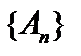 фундаментальна в
фундаментальна в 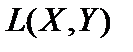 ,то последовательность норм
,то последовательность норм 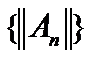 ограничена, то есть
ограничена, то есть 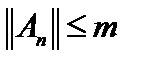 . С другой стороны,
. С другой стороны, 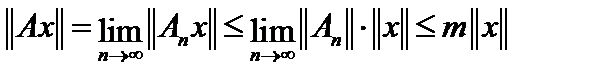 . Таким образом,
. Таким образом, 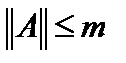 , и, следовательно, оператор
, и, следовательно, оператор 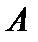 является непрерывным. В силу фундаментальности последовательности операторов
является непрерывным. В силу фундаментальности последовательности операторов 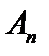 ,
, 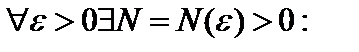
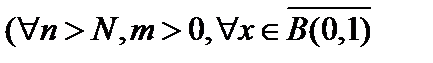
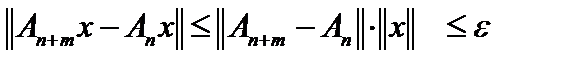 . Перейдем в данном неравенстве к пределу при
. Перейдем в данном неравенстве к пределу при 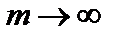 . Тогда
. Тогда 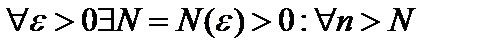 при условии
при условии 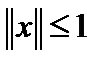 выполнится
выполнится 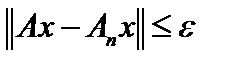 . Это значит, что
. Это значит, что 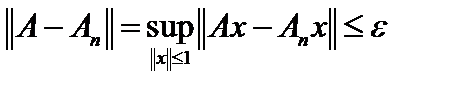 при всех
при всех 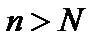 , то есть
, то есть 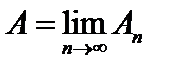 .
. 
Комментарий. В пространство линейных непрерывных операторов можно ввести и другие типы сходимости. Рассмотрим последовательность операторов ортогонального проецирования в гильбертовом пространстве. Пусть 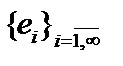 есть некоторый ортонормированный базис в гильбертовом пространстве
есть некоторый ортонормированный базис в гильбертовом пространстве 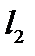 :
: 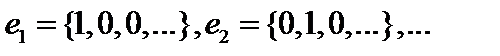 , и так далее. Тогдапроизвольный элемент
, и так далее. Тогдапроизвольный элемент 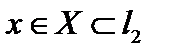 представим в виде ряда Фурье
представим в виде ряда Фурье 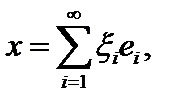 где
где 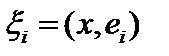 . Определим оператор проецирования
. Определим оператор проецирования 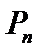 на подпространство
на подпространство 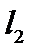 , натянутое на первые п элементов базиса, как
, натянутое на первые п элементов базиса, как 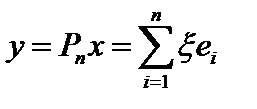 . Тогда
. Тогда 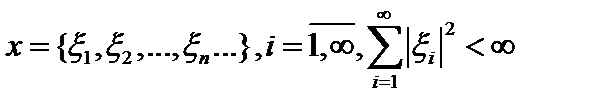 , а
, а 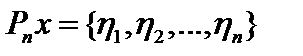 . То есть
. То есть 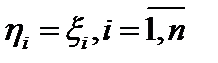 ,
, 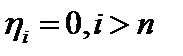 . Тогда
. Тогда 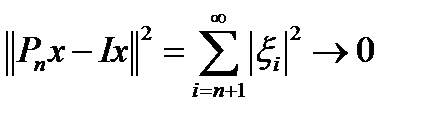 , как остаток сходящегося ряда, где
, как остаток сходящегося ряда, где 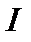
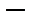 тождественный оператор. То есть
тождественный оператор. То есть 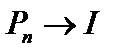 , но это какая-то другая сходимость, потому что равномерной сходимости нет. В самом деле, как только
, но это какая-то другая сходимость, потому что равномерной сходимости нет. В самом деле, как только 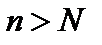 , то
, то 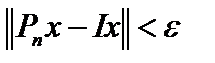 для любого
для любого 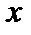 . Пусть
. Пусть 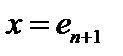 . Тогда
. Тогда 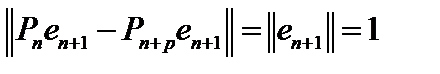 , так как
, так как 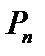 не сохраняет
не сохраняет 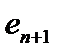 , а
, а 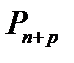 сохраняет. Это рассуждение подводит нас к следующему определению.
сохраняет. Это рассуждение подводит нас к следующему определению.
Определение 6. Последовательность операторов 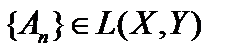 называется поточечно (сильно) сходящейся к оператору
называется поточечно (сильно) сходящейся к оператору 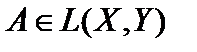 , если
, если 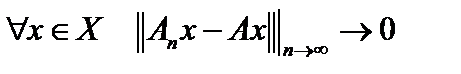 .
.
Комментарий. Поточечная сходимость означает сходимость в каждой точке пространства. Мы показали, что поточечная (сильная) сходимость последовательности операторов не влечет за собой, вообще говоря, равномерной сходимости этих же операторов. Обратное всегда верно: равномерная сходимость последовательности операторов всегда влечет за собой поточечную. Действительно, 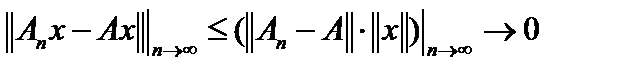 .
.
Будет ли пространство 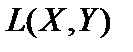 банаховым и в смысле поточечной сходимости? Покажем, что будет.
банаховым и в смысле поточечной сходимости? Покажем, что будет.
Теорема 6 (Принцип равномерной ограниченности Банаха  Штейнгауза). Пусть
Штейнгауза). Пусть 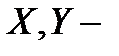 банаховы пространства, а последовательность
банаховы пространства, а последовательность 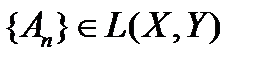 есть последовательность непрерывных линейных операторов, множество значений которых ограничено в любой точке
есть последовательность непрерывных линейных операторов, множество значений которых ограничено в любой точке 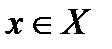 , то есть
, то есть 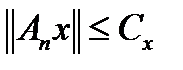 , где
, где 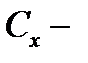 константы, быть может, различающиеся от точки к точке. Тогда числовая последовательность норм этих непрерывных линейных операторов
константы, быть может, различающиеся от точки к точке. Тогда числовая последовательность норм этих непрерывных линейных операторов 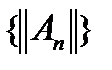 тоже ограничена, то есть
тоже ограничена, то есть 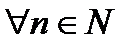 верно, что
верно, что 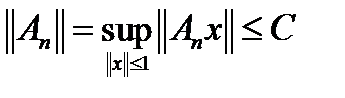 , где константа
, где константа 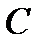 есть общая константа, то есть речь идёт об равномерной ограниченности.
есть общая константа, то есть речь идёт об равномерной ограниченности.
 Покажем сначала, что если
Покажем сначала, что если 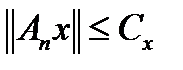 , то в замкнутом шаре
, то в замкнутом шаре 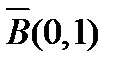 последовательность
последовательность 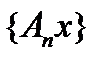 ограничена
ограничена 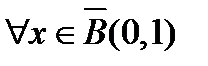 , то есть
, то есть 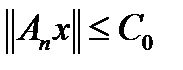 сразу
сразу 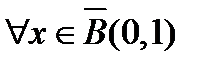 .
.
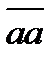 . Пусть последовательность
. Пусть последовательность 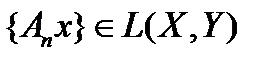 не ограничена ни в каком замкнутом шаре. Тогда она не ограничена и в шаре
не ограничена ни в каком замкнутом шаре. Тогда она не ограничена и в шаре 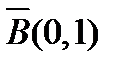 , равно как и в шаре
, равно как и в шаре 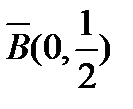 . Это значит, что существует элемент
. Это значит, что существует элемент 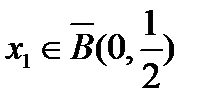 , на котором, начиная с номера
, на котором, начиная с номера 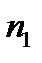 , норма
, норма 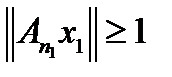 . Но оператор
. Но оператор 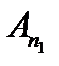 непрерывен, то есть это соотношение выполняется и в некотором замкнутом шаре
непрерывен, то есть это соотношение выполняется и в некотором замкнутом шаре 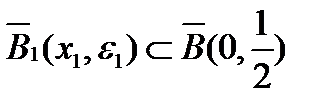 . Тогда для этого шара
. Тогда для этого шара 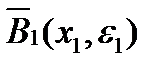 последовательность
последовательность 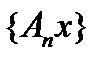 не ограничена и в шаре
не ограничена и в шаре 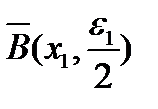 . То есть существует элемент
. То есть существует элемент 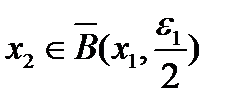 , на котором, начиная с номера
, на котором, начиная с номера 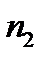 , норма
, норма 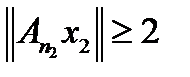 . Снова это неравенство выполняется и в некотором замкнутом шаре
. Снова это неравенство выполняется и в некотором замкнутом шаре 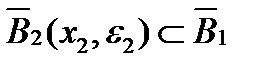 . Ясно, что существует точка
. Ясно, что существует точка 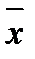 , которая принадлежит всем шарам
, которая принадлежит всем шарам 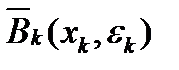 при условии, что
при условии, что 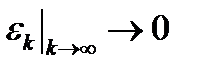 и в которой
и в которой 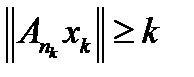 . Но это противоречит условию
. Но это противоречит условию 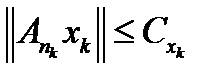 . То есть в замкнутом шаре
. То есть в замкнутом шаре 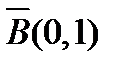 последовательность
последовательность 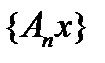 ограничена
ограничена 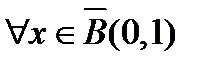 , то есть
, то есть 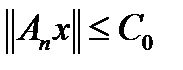 сразу
сразу 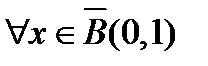 . Но тогда норма
. Но тогда норма 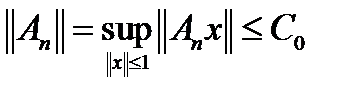 .
. 
Теорема 7. Пусть X и Y 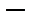 банаховы пространства. Тогда пространство
банаховы пространства. Тогда пространство 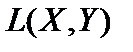 банахово в смысле поточечной сходимости.
банахово в смысле поточечной сходимости.
 Рассмотрим фундаментальную последовательность
Рассмотрим фундаментальную последовательность 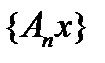 . Если последовательность
. Если последовательность 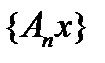 фундаментальна в каждой точке
фундаментальна в каждой точке 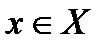 , а пространство
, а пространство 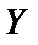 банахово, то она сходится в этой точке, то есть существует
банахово, то она сходится в этой точке, то есть существует 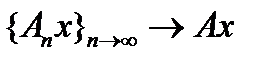 , то есть она ограничена, и ограничен, а следовательно, линеен оператор
, то есть она ограничена, и ограничен, а следовательно, линеен оператор 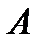 , то есть
, то есть 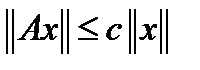 . Это как раз и означает, что любая поточечно сходящаяся фундаментальная последовательность непрерывных линейных операторов сходится к непрерывному линейному оператору, то естьпространство
. Это как раз и означает, что любая поточечно сходящаяся фундаментальная последовательность непрерывных линейных операторов сходится к непрерывному линейному оператору, то естьпространство 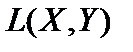 банахово в смысле поточечной сходимости.
банахово в смысле поточечной сходимости. 
Комментарий. В дальнейшем будем рассматривать банаховы пространств Комментарий. В дальнейшем будем рассматривать банаховы пространс
Определение 7. Пусть 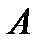 – оператор, вообще говоря, нелинейный,
– оператор, вообще говоря, нелинейный, 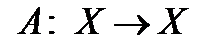 , где
, где 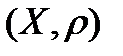 – полное метрическое пространство. Оператор
– полное метрическое пространство. Оператор 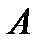 называется сжимающим если существует константа q:
называется сжимающим если существует константа q: 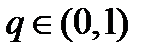 , такая, что для любых
, такая, что для любых 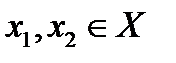 имеет место неравенство
имеет место неравенство 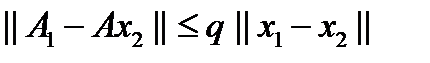 .
.
Комментарий. Всякое сжимающее отображение непрерывно.
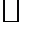 Пусть
Пусть 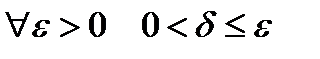 тогда как только
тогда как только 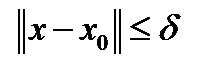 , имеем:
, имеем: 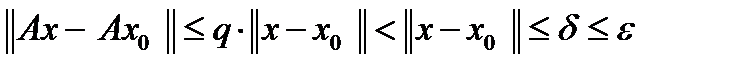 . Таким образом, оператор
. Таким образом, оператор 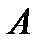 непрерывен.
непрерывен. 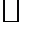
Определение 8. Элемент 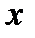 называется неподвижной точкой оператора
называется неподвижной точкой оператора 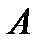 , если
, если 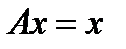 .
.
Теорема 7 (Принцип сжимающих отображений Банаха). Сжимающее отображение 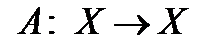 полного метрического пространства
полного метрического пространства 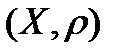 в себя имеет единственную неподвижную точку
в себя имеет единственную неподвижную точку 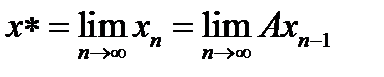 .
.

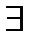 . Пусть точка
. Пусть точка 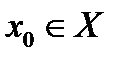 . Составим последовательность
. Составим последовательность
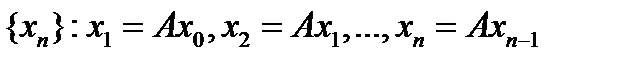 и покажем, что она фундаментальна.
и покажем, что она фундаментальна. 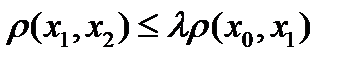 ,
, 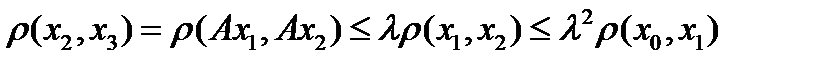 , Тогда
, Тогда 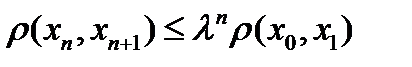 и так далее. Последовательно применяя неравенство треугольника, получим
и так далее. Последовательно применяя неравенство треугольника, получим
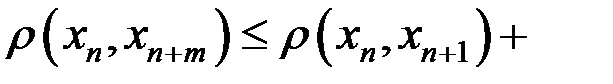
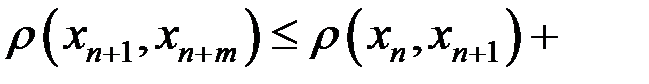
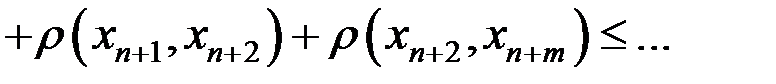
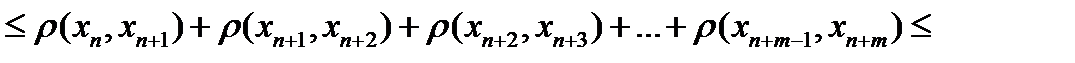
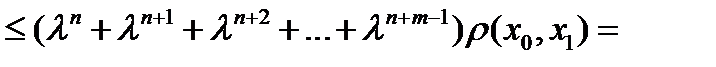
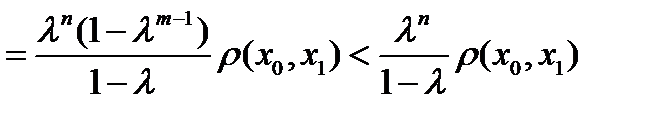 . (5)
. (5)
Так как 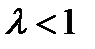 , то
, то 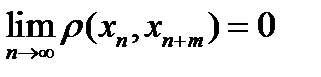 , то есть последовательность
, то есть последовательность 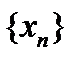 фундаментальна. А поскольку метрическое пространство
фундаментальна. А поскольку метрическое пространство 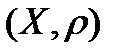 полное, то
полное, то 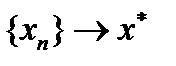 . Покажем, что
. Покажем, что 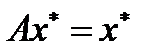 . Так как
. Так как 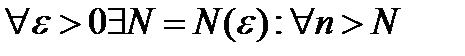 выполнено
выполнено 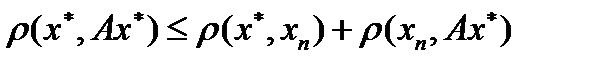
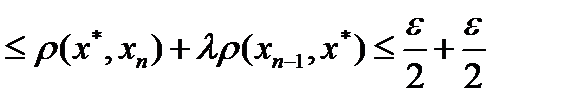 .
.
