Предел, непрерывность, дифференцируемость ФНП

Число А назыв.пределом функции z=f(x;y) при М(х;у) стремящемся к М₀(х0,у0) если для любого положительного числа εсуществует такое положительное число r ,что для всех точек М(х;у) попадающих внутрь круга радиуса r с центром в точке М₀ выполняется неравенство:

│f(x;y)-A│<ε

Обозначение:

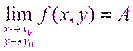
Функция z=f(x;y) назыв.непрерывной в точке M₀ если существует конечный предел 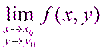и он равен значению функции в этой точке.

lim f(x;y)=f(x₀;y₀)

Функция назыв.непрерывной на множестве D если для любой точки М(х;у) из D выполнено равенство lim f(x;y)=f(x₀;y₀)

Разность f(x+∆x;y)-f(x;y) называют частным приращением функции z=f(x;y) по переменной х.

Разность f(x;y+∆у)-f(x;y) называют частным приращением функции z=f(x;y) по переменной у.

ФНП наз. Дифференцируемой на некотором мн-ве D если в каждой точке этого мн-ва она имеет полный дифференциал(dz)

Частные производные первого порядка ФНП.

Частными производными 1-го порядка функции z по переменным х и у назыв. пределы отношения частных приращений функции z(x;y) к соответствующим приращением аргумента.

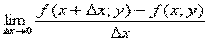=z’_x

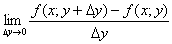= z’_y

Замечания:1)при вычислении частных производных по одной из переменных вторая переменная считается константой.2)вычисления частных производных выполняется по тем же правилам, что и вычисления производной функции одной переменной

Полное приращение и полный дифференциал ФНП.

Разность f(x₀+∆x;y₀+∆y)-f(x₀;y₀) назыв.полным приращением функции и обозначается ∆z: ∆z= f(x₀+∆x;y₀+∆y)-f(x₀;y₀)

На малых приращениях аргумента (∆x стремится к 0 и ∆y стремится к 0) полное приращение функции приблизительно равно полному дифференциалу.∆z приблизительно равно dz.

Это используется при вычислении приближенных значений.По формуле:

f(x0+∆x;y0+∆y) приблизительно равно f(x0;y0)+z’_x(x0;y0)∆x+z’_y (xo;y0)∆y

Полным дифференциалом первого порядка функции z назыв.выражение dz=z’_xdx+z’_ydy

Частные производные и дифференциалы высших порядков ФНП.

Частные производные по х и по у вычисленные от частных производных 1-го порядка функции z(z’_x и z’_y) назыв.частными производными второго порядка функции z=f(x;y) и обозначаются:z”_x²=(z’_x)’_x ; z”_xy=(z’_x)’y; z”_y²=(z’_y)’_y ; z”_yx=(z’_y)’_x

Дифференциалом 2-го порядка ФНП z=f(x;y) назыв.выражение d²z=d(dz)=z”_x²dx²+2z”_xydxdy+z”_y²dy²

Локальные экстремумы ФНП.

Точка М₀(х₀;у₀) назыв. Точкой локального максимума или локального минимума функции z=f(x;y) если существует такая окружность с центром в точке М₀ и радиусом эпсилон ,что для всех точек М(х;у) попадающий внутрь этой окружности выполняется неравенство:f(M)<f(M₀) или f(M)>f(M₀).

Значение функции в точках локального максимума и локального минимума назыв.максимумами и минимумами функции.

z_max =z(M₀) или z_min =z(M₀)

Точки локального максимума и минимума назыв.точками локального экстремума, а значение функции в этих точках назыв.экстремумом ФНП.

Теорема(необходимое условие экстремума)

Если функция z=f(x;y) дифференцируема в точке М₀(х₀;у₀) имеет в этой точке экстремум, то частные производные 1-го порядка вычисленные в этой точке=0 , то есть : z’_x(М₀)=0; z’_y(М₀)=0.

Точки удовлетворяющие этому условию назыв.критическими.

Теорема(достаточный признак существования экстремума)

Если точка М₀(х₀;у₀)-критическая точка функции z=f(x;y) и z”_x²(M₀)=A, z”_xy(M₀)=B, z”_y²(M₀)=C то в критической точке

экстремум есть, если AC-B²>0 , A<0-максимум, при А>0-минимум

экстремума нет если AC-B²<0