Обробка результатів вимірювання. Мета роботи: ознайомитися з методом визначення прискорення вільного падіння за допомогою математичного маятника та дослідити властивості розподілу випадкових

Київ, 2012р.

Мета роботи: ознайомитися з методом визначення прискорення вільного падіння за допомогою математичного маятника та дослідити властивості розподілу випадкових величин.

Завдання:

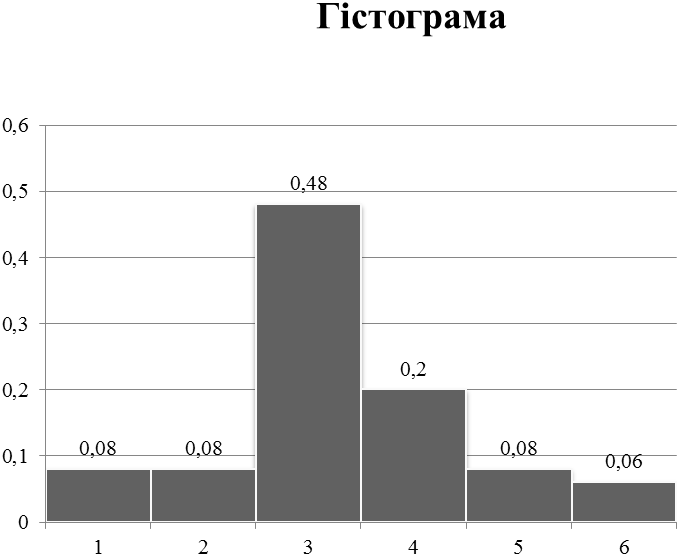
1. Побудувати гістограму виміряних значень періоду коливань.

2. За допомогою математичного маятника експериментально визначити прискорення вільного падіння біля поверхні Землі.

Прилади: математичний маятник, секундомір, рулетка.

Теоретичні відомості

Нормальний розподіл випадкових величин

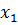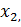
Теорія випадкових похибок базується на теорії ймовірностей, яка розглядає випадкові події. Імовірність появи деякої події дорівнює відношенню кількості випадків ∆n, за яких подія настає, до загальної кількості спостережень n. Вважатимемо, що маємо справу лише з випадковими похибками. 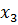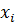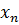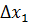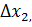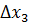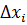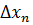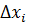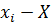Тобто при повторних вимірюваннях деякої величини x ми одержали низку значень цієї величини, , … , … та похибок , … , … , де = є абсолютною похибкою значення хі стосовно істинного значення величини X.

Якщо випадкові похибки невеликі за значеннями, то вони здебільшого підлягають закону нормального розподілу. Цей закон має місце за виконання таких умов:

1) випадкові похибки набирають низку неперервних значень;

2) за великої кількості вимірювань однаково часто трапляються додатні й від'ємні похибки однакової величини;

3) малі похибки трапляються частіше, ніж великі.

Аналітичний вираз для нормального розподілу вперше був одержаний німецьким математиком Гаусом, і має назву розподіл Гауса. Формула розподілу Гауса (розподілу ймовірностей) має вигляд:

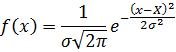
де 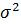— дисперсія (розсіяння) виміряної величини, тоді дістанемо середньоквадратичне відхилення σ, що дорівнює середньоквадратичній похибці окремого вимірювання:

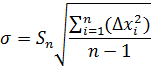
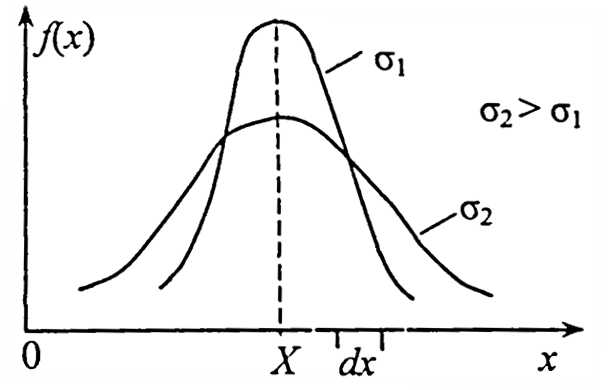
Функція f(x) називається щільністю ймовірності — імовірністю потрапляння величини х у деякий одиничний інтервал dx (dx=1) на осі х. Якщо ж інтервал dx є довільним, то функцію розподілу ймовірностей можна подати як:

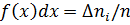
де 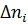— кількість вимірювань в інтервалі від 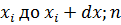— загальна кількість вимірювань.

Функція розподілу ймовірностей (закон нормального розподілу) графічно може бути зображена кривою Гауса. Імовірність появи малих похибок є більшою, ніж великих. Ця ймовірність також збільшується з покращанням якості вимірювання, що визначається дисперсією. Чим менша дисперсія ( 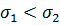), тим менший розкид похибок, і тим більша точність вимірювання.

Математичний маятник

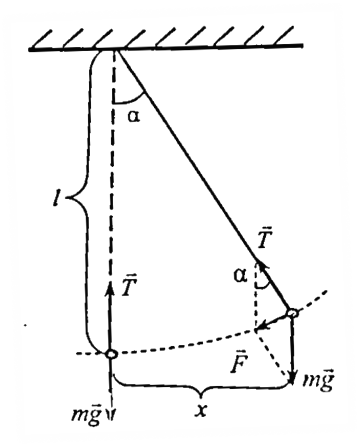Математичний маятник — ідеальна модель маятника (матеріальна точка, підвішена на невагомій і нерозтяжній нитці). На практиці це металева куля масою m, підвішена на міцній нитці довжиною l, при цьому довжина нитки набагато більша за розміри кулі. Такий маятник , відхилений від положення рівноваги на кут 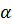і залишений без дії зовнішніх сил, буде виконувати коливання, які приблизно можна вважати незгасаючими. Зворотна сила F напрямлена по дотичній до траєкторії в бік рівноваги, вона є рівнодійною сили натягу нитки Т та сили тяжіння mg. Якщо кут 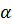достатньо малий (З ... 6°), то в радіанній мірі 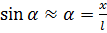, де х — зміщення маятника від положення рівноваги. З рисунка видно, що

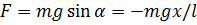
Знак «мінус» свідчить, що сила і зміщення напрямлені в протилежні боки. За другим законом Ньютона

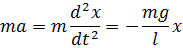
Позначимо 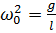, тоді

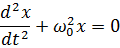
Ми дістали диференціальне рівняння коливань маятника (головне рівняння гармонічних коливань). Його розв'язок відносно 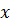має вигляд:

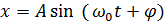
де А — амплітуда коливань, 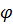— початкова фаза коливань, 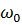— циклічна частота (кількість коливань за час 2 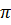секунд).

Період (час одного коливання) 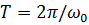, або 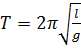, звідки .

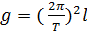Із цієї формули випливає, що, знаючи довжину маятника і період його коливання, можна обчислити прискорення вільного падіння в тій точці Землі, де міститься маятник.

Прискоренням вільного падіння називається прискорення, з яким рухається тіло під дією єдиної сили — сили тяжіння 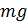. Тому, використовуючи закон всесвітнього тяжіння, можна теоретично встановити, від чого залежить величина прискорення вільного падіння

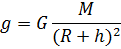
де G — гравітаційна стала; М — маса планети; R — радіус планети; h — висота тіла над поверхнею планети.

Висновок: величина прискорення вільного падіння залежить тільки від величин, якими визначається сила всесвітнього тяжіння, і не залежить від параметрів конкретного математичного маятника.

Порядок виконання роботи

1. Виміряти рулеткою довжину маятника, тобто відстань від точки підвісу нитки до центра кульки. Отриманий результат записати в протокол.

2. Відхилити кульку маятника на кут 3-5° від положення рівноваги і відпустити її.

3. Почекати, поки кулька зробить 5-7 повних коливань. Цей час потрібен, для того щоб згасли другорядні коливання, які з'явилися при виведенні маятника з положення рівноваги.

4. Увімкнути секундомір, коли кулька проходить положення рівноваги, і вимкнути секундомір, коли маятник зробить три-п'ять повних коливань. Одержаний результат записати в таблицю.

5. Не зупиняючи маятника, повторити п. 4 п'ятдесят разів. Якщо за час проведення вимірювань амплітуда коливань суттєво зменшиться і проводити вимірювання буде незручно, треба повторити п. 2 і 3, потім продовжити вимірювання за п. 4.

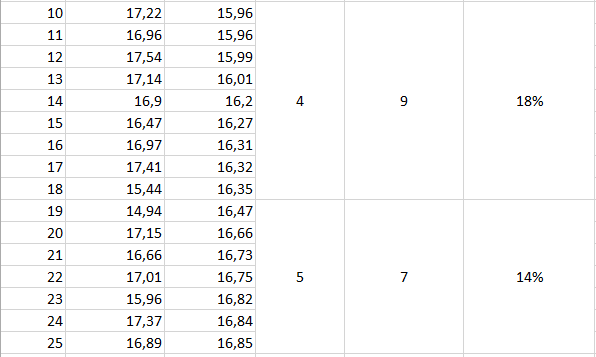
Обробка результатів вимірювання

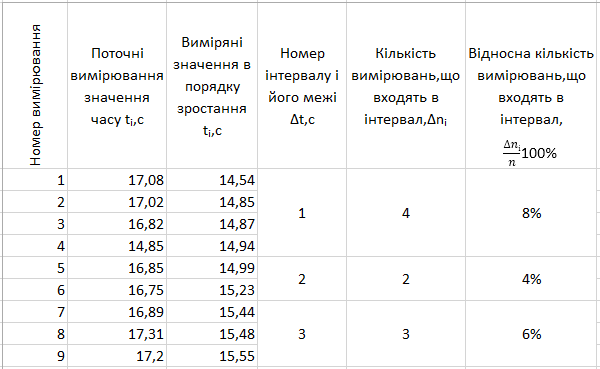
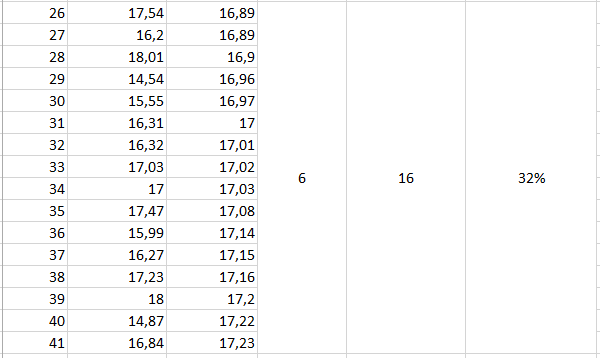
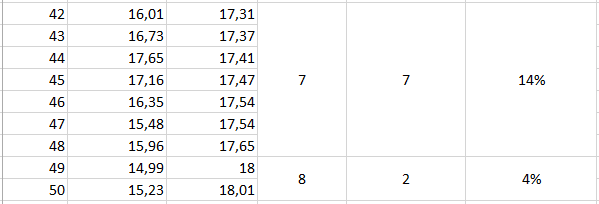
1. Обчислення діапазону ∆t та ділення його на 7 однакових інтервалів:

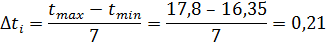
2. Визначення меж кожного з інтервалів:

t+∆t_і=16,35+0,21=16,56+0,21=16,77+0,21=16,98+0,21=17,19+0,21=17,4+0,21=

=17,61+0,21=17,82

І. 16,35-16,56

ІІ. 16,57-16,77

ІІІ. 16,78-16,98

ІV. 16,99-17,19

V. 17,2-17,4

VI. 17,41-17,61

VII. 17,62-17,82

3. Середньоарифметичне значення часу <t> серед вимірювань, що входять в інтервал 3: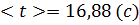

4. Обчислення прискорення вільного падіння :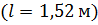

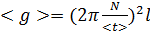
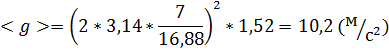
5. Обчислення абсолютної похибки вимірювання часу коливання маятника за даними, що входять до інтервалу 3: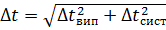

:

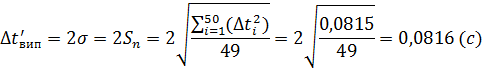
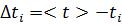∆t₁=16,88-16,79 =0,09

∆t₂=∆t₃=∆t₄=∆t₅=∆t₆=16,88-16,8= 0,08

∆t₇=∆t₈=∆t₉=∆t₁₀=∆t₁₁=16,88-16,85=0,03

∆t₁₂=16,88-16,86=0,02

∆t₁₃=16,88-16,87=0,01

∆t₁₄=16,88-16,88=0

∆t₁₅=∆t₁₆=16,88-16,91=-0,03

∆t₁₇=∆t₁₈=16,88-16,92=-0,04

∆t₁₉=16,88-16,93=-0,05

∆t₂₀=∆t₂₁=∆t₂₂=16,88-16,94=-0,06

∆t₂₃=16,88-16,97=-0,09

∆t₂₄=16,88-16,98=-0,1

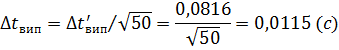
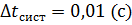
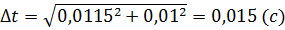
За Стьюдентом:

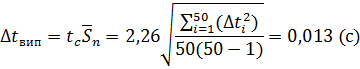
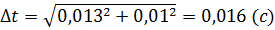
6. Обчислення відносної похибки вимірювання прискорення вільного падіння :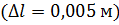

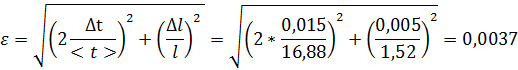
7. Обчислення абсолютної похибки вимірювання прискорення вільного падіння:

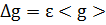
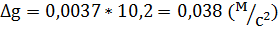
8. Остаточний результат:

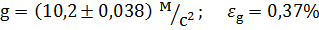
Висновки

Виконавши цю лабораторну роботу, я навчився визначати прискорення вільного падіння за допомогою математичного маятника, яка за моїми обчисленнями дорівнює g=10,2 ^м/_с² з допущенням похибки у 0,37%. З побудованої гістограми зрозуміло, що найбільша кількість вимірюваних значень належить інтервалу 3 (16,78-16,98с).

Перевірка гіпотези про нормальний розподіл

експериментальних даних

№	ti	Xi	Yi	№	ti	Xi	Yi
	16,92	0,49020			17,06	0,74510	0,674
	16,92	0,50980	0,025		17,1	0,76471	0,706
	16,93	0,52941	0,075		17,1	0,78431	0,772
	16,94	0,54902	0,125		17,1	0,80392	0,841
	16,94	0,56863	0,176		17,1	0,82353	0,915
	16,94	0,58824	0,227		17,2	0,84314	0,994
	16,97	0,60784	0,279		17,22	0,86275	1,0803
	16,98	0,62745	0,331		17,27	0,88235	1,174
	16,99	0,64706	0,385		17,4	0,90196	1,281
	17,03	0,66667	0,439		17,52	0,92157	1,405
	17,04	0,68627	0,495		17,54	0,94118	1,554
	17,05	0,70588	0,553		17,61	0,96078	1,75
	17,06	0,72549	0,612		17,8	0,98039	2,053