Критерий устойчивости Михайлова

Предложенный в 1938 г. А.В. Михайловым критерий позволяет судить об устойчивости системы по кривой, построенной на основании характеристического полинома замкнутой системы.

Рассмотрим замкнутую систему, характеристическое уравнение которой имеет вид:

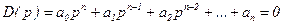, (6.20)

Задача состоит в определении условий, при которых все корни этого уравнения (р₁; р₂; р_n) будут иметь отрицательные вещественные части.

Полином D(p) можно представить в виде:

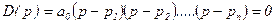, (6.21)

где

p_n - корни уравнения (6.20)

Положим p=jv, тогда

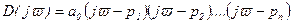. (6.22)

Каждая из скобок этого выражения представляет собой комплексное число. Следовательно, D(jv) представляет собой произведение n комплексных чисел. При перемножении аргументы комплексных чисел складываются.

На рисунке 6.4,а дано геометрическое представление комплексных чисел (jv-p_n) на комплексной плоскости p. Начала векторов, изображающих комплексные числа, лежат в точках p_n, а концы - на мнимой оси в точке jv. На рисунках 6.4, б, в представлена картина перемещения вектора (jv-p_n) при изменении v от нуля до бесконечности для случая, когда вещественная часть p_n корня отрицательная (рисунок 6.4, б) и положительная (рисунок 6.4, в). Очевидно, что в первом случае угол поворота вектора составил 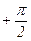, во втором случае вектор повернется в отрицательном направлении на угол 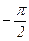. Результирующий угол поворота вектора D(jv) при изменении v от 0 до ¥ будет равен сумме углов поворота отдельных сомножителей (6.22).

.

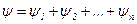Очевидно, если все корни левые, что является необходимым и достаточным условием устойчивости, то суммарный угол поворота вектора D(jw) составит:

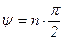, (6.23)

где n - порядок характеристического уравнения замкнутой системы.

Геометрическое место точек, которые последовательно проходит конец вектора D(jw) при изменении v от нуля до бесконечности, называется кривой (годографом) Михайлова или годографом характеристического вектора.

Учитывая это, критерий устойчивости Михайлова можно сформулировать следующим образом.

Для того, чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы вектор годографа Михайлова замкнутой системы при изменении частоты v от 0 до +¥, начав движение из точки, лежащей на положительной вещественной оси и вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол .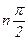

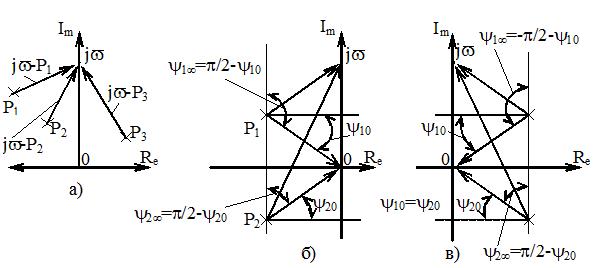
Рисунок 6.4

а) геометрическое представление комплексных чисел (jv-p_n) на комплексной плоскости p; б) перемещения вектора (jv-p_n) при изменении v от нуля до бесконечности для случая, когда вещественная часть p_n корня отрицательная; в) перемещения вектора (jv-p_n) при изменении v от нуля до бесконечности для случая, когда вещественная часть p_n корня положительная

На рисунке 6.5, а показаны годографы для устойчивых систем, описываемых уравнениями 1-5-го порядков. Годографы для неустойчивых и находящихся на границе устойчивости систем представлены соответственно на рисунке 6.5, б, в.

Анализируя годографы Михайлова, можно установить следующее: в устойчивой системе управления при последовательном прохождении кривой Михайлова квадрантов координатной плоскости вещественная и мнимая оси пересекаются ею поочередно. Поэтому значения частот, при которых происходит пересечение кривой с вещественной или мнимой осью, должны являться корнями уравнений

U(v)=0,

V(v)=0.

В связи с указанным следствием, можно привести другую формулировку критерия устойчивости Михайлова: система автоматического управления будет устойчива тогда и только тогда, когда вещественная U(v) и мнимая V(v) функции Михайлова, приравненные к нулю, имеют все действительные и перемежающиеся корни, причем общее число этих корней равно порядку характеристического уравнения n, и при v=0 удовлетворяются условия U(v)>0, V(v)>0.

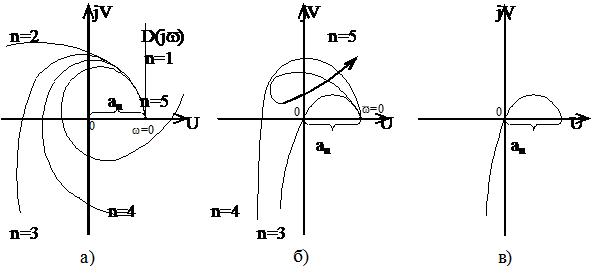
Рисунок 6.5 Годографы Михайлова:

а - устойчивых систем от 1-го (n=1) до 5-го (n=5) порядков; б - неустойчивых систем; в – системы, находящейся на границе устойчивости

Произведем анализ устойчивости САР, принципиальная схема которой приведена на рисунке 6.3. Так же как и в предыдущем случае полагаем, что гибкая отрицательная обратная связь по току отсутствует, т.е. структурная схема имеет вид, представленный на рисунке 6.6.

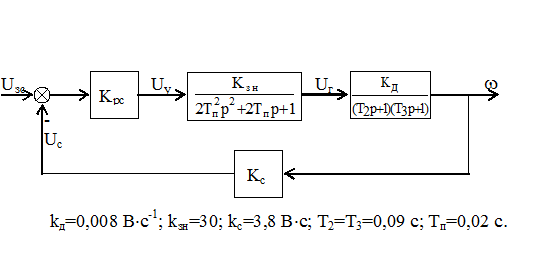
Рисунок 6.6 Структурная схема САРС

Передаточная функция замкнутой системы автоматического регулирования скорости (САРС)

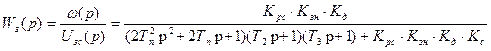(6.24)

Характеристическое уравнение замкнутой САРС

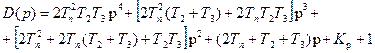
Подставляя численные значения и принимая K_рс=15, получим:

,

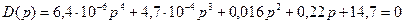т.е. если

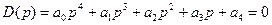, то ;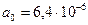

; ; ; .

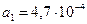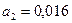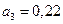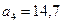Подставляя p=jv, получим

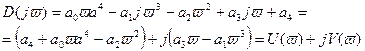
Подставляя численные значения, получим:

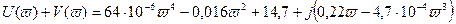(6.25)

Имеем:

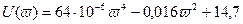; (6.26)

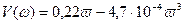. (6.27)

Составим таблицу при изменении v :

Таблица 6.1

v	0	5	10	15	20	25	30	35	40	45	50	21,6
U(v)	14,7	14,3	13,16	11,4	9,3	7,2	5,5	4,7	5,5	8,5	14,7	8,6
V(v)	0	1,04	1,7	1,71	0,64	-1,8	-6,1	-12,5	-21	-33	-47,7	0

Годограф Михайлова, описываемый уравнением (6.25) представлен на рисунке 6.7 (кривая 1). Видно, что исследуемая САР неустойчива. Из (6.25÷6.27) следует, что для замкнутой САР свободный член a_n получается при v=0 и определяет начало кривой Михайлова. Очевидно, что величина a_n не влияет на форму годографа, так как не содержит v, а смещает его вдоль по вещественной оси. Следовательно, изменяя a_n можно добиться устойчивости САР, перемещая годограф влево по вещественной оси. Как видно из рисунка 6.7 при 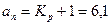САР находится на границе устойчивости. Нетрудно определить критический коэффициент усиления разомкнутой системы 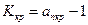. Для этого достаточно определить разность координат начала годографа и точки пересечения его с осью абсцисс, а затем из этой разности вычесть единицу. В нашем случае

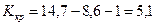. (6.28)

Соответствующий этому значению коэффициент передачи регулятора скорости

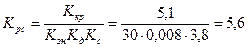, (6.29)

Такие же выводы можно получить и не строя годографа, а воспользовавшись условием перемежаемости корней.

Рисунок 6.7 Астатические амплитудно-фазовые частотные характеристики САУ

Для этого достаточно найти корни уравнения V(v)=0. При этом корни с отрицательными значениями во внимание не принимаются, так как относятся к не рассматриваемому участку -¥<v<0. В нашем случае для уравнения

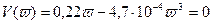
находим: v₁=0, v₂=21,63.

Если эти значения подставлять поочередно в уравнение U(v), то мы должны получить для устойчивой системы U(v₁)>0 и U(v₂)<0; для системы, находящейся на границе устойчивости U(v₁)=U(v₂)>0. Это положение наглядно иллюстрируется таблицей представленной на рисунке 6.7. Сопоставление результатов исследований (6.26, 6.27) и (6.28, 6.29) дает основание сделать еще один важный вывод.

Пренебрежение более высокими порядками в дифференциальных уравнениях, описывающих поведение отдельных элементов САУ, может привести к значительным погрешностям в оценке динамических характеристик САУ. В данном случае пренебрежение вторым порядком в уравнении (6.11) привело к разности результатов исследований одной и той же системы в 1,7 раз.