Плоские и сферические гармонические волны
Конкретный вид волновой функции ξ(x, t) плоской волны определяется условиями возникновения волны – источником волны. Если источник, находящийся в начале координат (в плоскости x = 0), совершает гармонические колебания
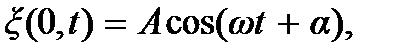
то создаваемая им волна называется гармонической. Чтобы получить формулу этой волны следует в формуле колебаний заменить t на 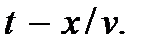 Будем иметь
Будем иметь
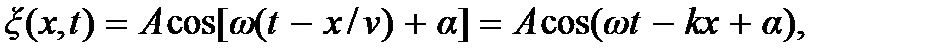 (9.7)
(9.7)
где 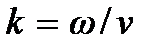 – так называемое волновое число. Соотношение (9.7) называется формулой плоской гармонической волны, распространяющейся вдоль оси X. Плоская гармоническая волна, формально описываемая функцией (9.7), как и сама эта функция, является бесконечной во времени
– так называемое волновое число. Соотношение (9.7) называется формулой плоской гармонической волны, распространяющейся вдоль оси X. Плоская гармоническая волна, формально описываемая функцией (9.7), как и сама эта функция, является бесконечной во времени 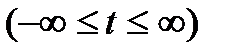 и безграничной в пространстве
и безграничной в пространстве 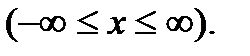
В формуле (9.7) А – амплитуда волны, ω – частота волны. Аргумент косинуса, т.е. функция 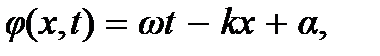 называется фазой волны,
называется фазой волны, 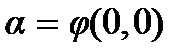 – начальной фазой. Заметим, что амплитуда и частота (а значит, и период Т) волны равны амплитуде и частоте (и периоду) колебаний источника. Фаза волны, в отличие от фазы колебаний источника, зависит также и от расстояния x волнового фронта до источника. Это показывает, что волна – процесс, развивающийся в пространстве и во времени. Функция(6.3), описывающая волновой процесс, является не только периодической функцией времени, но также и периодической функцией координаты x. Следовательно, волна является процессом, периодическим в пространстве и во времени. Период во времени Т определяется так же, как и период колебаний. Так как период косинуса равен 2π, то, как легко убедиться, величина смещения
– начальной фазой. Заметим, что амплитуда и частота (а значит, и период Т) волны равны амплитуде и частоте (и периоду) колебаний источника. Фаза волны, в отличие от фазы колебаний источника, зависит также и от расстояния x волнового фронта до источника. Это показывает, что волна – процесс, развивающийся в пространстве и во времени. Функция(6.3), описывающая волновой процесс, является не только периодической функцией времени, но также и периодической функцией координаты x. Следовательно, волна является процессом, периодическим в пространстве и во времени. Период во времени Т определяется так же, как и период колебаний. Так как период косинуса равен 2π, то, как легко убедиться, величина смещения 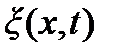 не изменится, если в формуле (6.3) заменить t на
не изменится, если в формуле (6.3) заменить t на 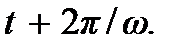 Следовательно период волны во времени
Следовательно период волны во времени 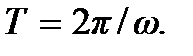 Чтобы определить период волны в пространстве, заметим, что смещения
Чтобы определить период волны в пространстве, заметим, что смещения 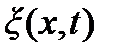 не изменится, если в формуле (6.3) заменить x на
не изменится, если в формуле (6.3) заменить x на 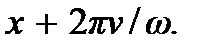 Отсюда находим пространственный период волны. Обозначив его через λ, получим
Отсюда находим пространственный период волны. Обозначив его через λ, получим 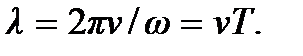 Пространственный период волны называют ее длиной волны. Как видим, длина волны – это расстояние, на которое распространяется волна за один период колебаний частиц. Поскольку длина волны зависит от скорости волны, а скорость в разных средах разная, то и длина волны будет различной для разных сред.
Пространственный период волны называют ее длиной волны. Как видим, длина волны – это расстояние, на которое распространяется волна за один период колебаний частиц. Поскольку длина волны зависит от скорости волны, а скорость в разных средах разная, то и длина волны будет различной для разных сред.
Волновое число можно выразить через длину волны:
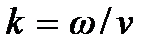 =
= 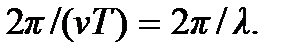
Следовательно, волновое число – это число длин волн, укладывающихся на отрезке диной 2π.
Зафиксируем какое-либо значение фазы волны (6.3), т.е. положим 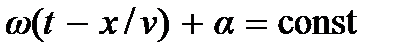 и продифференцируем это выражение по времен t. Тогда получим
и продифференцируем это выражение по времен t. Тогда получим 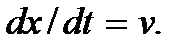 Скорость
Скорость 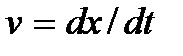 есть скорость, с которой перемешается зафиксированное значение фазы. Следовательно, скорость волны v представляет собой скорость переноса фазы, и поэтому ее называют фазовой скоростью волны.
есть скорость, с которой перемешается зафиксированное значение фазы. Следовательно, скорость волны v представляет собой скорость переноса фазы, и поэтому ее называют фазовой скоростью волны.
Формулу плоской волны, распространяющейся вдоль оси X, легко обобщить на случай волны, распространяющейся в произвольном направлении. Пусть это направление определяется единичным вектором n и пусть r – радиус-вектор некоторой точки пространства. Проведем через эту точку волновую поверхность. В рассматриваемом случае плоской волны такой поверхностью будет плоскость, перпендикулярная направлению n (рис. 9.1). В рассмотренном выше случае n = {1, 0, 0} и, следовательно, ска-
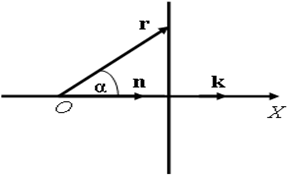 Рис. 9.1 Рис. 9.1 |
лярное произведение n∙r = =rcos𝛼 представляет собой проекцию радиус-вектора r на ось X, так что x = n∙r. Введем в рассмотрение так называемый волновой вектор k, определив его как k = kn.Модуль этого вектора равен волновому числу k, а его направление совпадает с направлением распространения волны n. Тогда 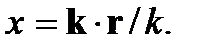 Подставив это в формулу (6.3), получим формулу волны, распространяющейся в произвольном направлении (направлении, определяемым волновым вектором k):
Подставив это в формулу (6.3), получим формулу волны, распространяющейся в произвольном направлении (направлении, определяемым волновым вектором k):
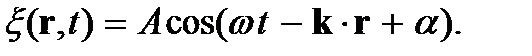 (9.4)
(9.4)
Если зафиксировать значение фазы в момент времени t, то получим 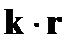 = const. Это есть уравнение плоскости, перпендикулярной волновому вектору k. Волна (6.4), как и любая волна вида
= const. Это есть уравнение плоскости, перпендикулярной волновому вектору k. Волна (6.4), как и любая волна вида 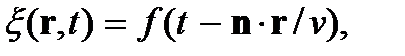 удовлетворяет волновому уравнению
удовлетворяет волновому уравнению
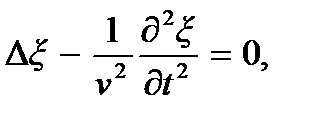 (9.5)
(9.5)
где 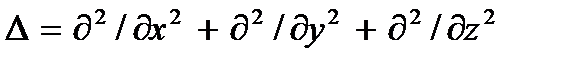 – так называемый оператор Лапласа.
– так называемый оператор Лапласа.
Как и гармонические колебания, гармонические волны можно записать в комплексной форме. Для плоской волны (6.4) будем иметь
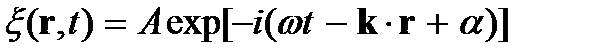 .
.
Символ реальной части Re при этом опускается.
Сферические волны распространяются равномерно по всем направлениям от точечного источника, находящегося в начале координат, и описываются функцией вида
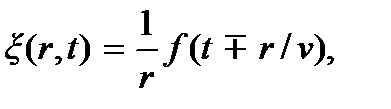
где знак минус соответствует расходящейся сферической волне, а плюс – сходящейся, 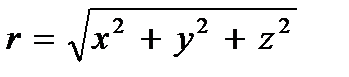 – расстояние от точечного источника волн до точки, расположенной на волновом фронте (радиус сферической волны). Поверхность постоянной фазы
– расстояние от точечного источника волн до точки, расположенной на волновом фронте (радиус сферической волны). Поверхность постоянной фазы 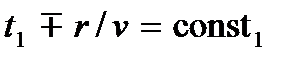 представляет собой сферу r = const. Множитель
представляет собой сферу r = const. Множитель 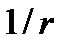 учитывает тот факт, что суммарная энергия колебаний частиц среды, расположенных на сферических волновых поверхностях, должна быть одинаковой для разных радиусов r поверхностей.
учитывает тот факт, что суммарная энергия колебаний частиц среды, расположенных на сферических волновых поверхностях, должна быть одинаковой для разных радиусов r поверхностей.
Формула сферической гармонической волны имеет вид
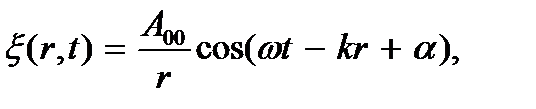
где А00 – амплитуда волны на расстоянии 1 м от источника. Функция 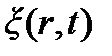 удовлетворяют волновому уравнению (6.5) с лапласианом, выраженным в сферической системе координат. В комплексной форме сферическая волна будет иметь вид
удовлетворяют волновому уравнению (6.5) с лапласианом, выраженным в сферической системе координат. В комплексной форме сферическая волна будет иметь вид
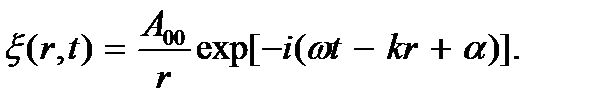
Функцию 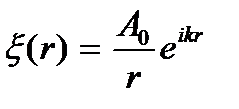 называют комплексной амплитудой сферической волны;
называют комплексной амплитудой сферической волны; 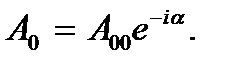 Сферические волны удовлетворяют волновому уравнению
Сферические волны удовлетворяют волновому уравнению
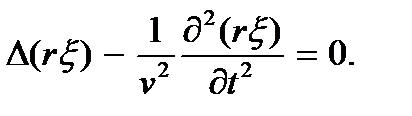
При этом оператор Лапласа Δвыражается через ссферические координаты.
Перенос энергии волной
Поскольку волна – это процесс распространения колебаний в пространстве, а колебания обладают энергией, то распространение волны в каком-либо направлении в пространстве сопровождается переносом энергии колебаний в этом направлении. Рассмотрим характеристики переноса энергии волной. При распространении волны каждый элемент объема волнового поля будет обладать энергией. Выделим в волновом поле элементарный объем dV. В этом объеме будет заключена энергия колебаний dW. Величина 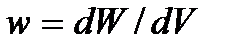 называется объемной плотностью энергии волнового поля. Найдем эту величину.
называется объемной плотностью энергии волнового поля. Найдем эту величину.
Объем среды, в котором распространяется волна, обладает кинетической и потенциальной энергиями колебаний частиц. Выделим в среде частицу объемом ΔV и массой Δm. Ее кинетическая энергия
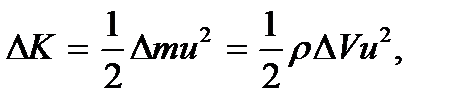
где 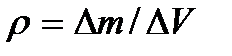 – плотность среды,
– плотность среды, 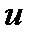 – скорость колебаний частицы.
– скорость колебаний частицы.
Используя формулу волны (7.3). Тогда скорость частицы
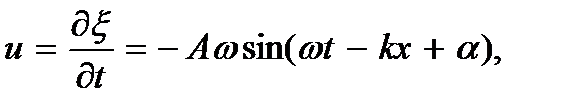
а ее кинетическая энергия
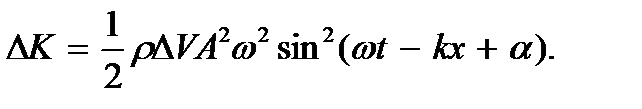
Для определения потенциальной энергии волны заметим, что энергия упруго деформированного элемента объемом 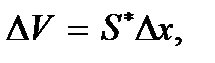 где
где 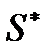 – площадь поперечного сечения,
– площадь поперечного сечения, 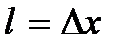 – длина выделенного объема, может быть представлена в виде U = =
– длина выделенного объема, может быть представлена в виде U = = 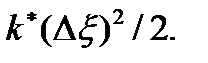 Здесь учтено, что абсолютная деформация Δl при сжатии или растяжении элемента длиной Δx равна
Здесь учтено, что абсолютная деформация Δl при сжатии или растяжении элемента длиной Δx равна 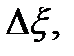 т.е. разности смещений концов элемента,
т.е. разности смещений концов элемента, 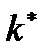 – жесткость элемента. С учетом этого получаем
– жесткость элемента. С учетом этого получаем
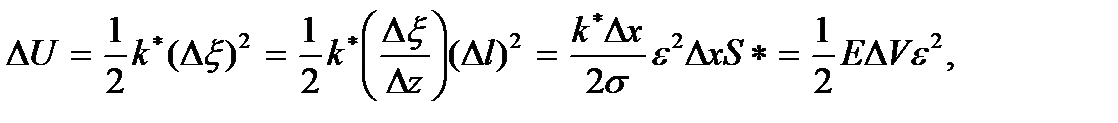 (9.6)
(9.6)
де 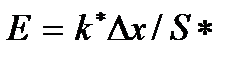 – модуль Юнга,
– модуль Юнга, 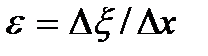 – относительная деформация элемента Δx, которая при
– относительная деформация элемента Δx, которая при 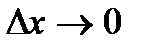 в случае волны переходит в частную производную от
в случае волны переходит в частную производную от 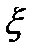 по x:
по x:
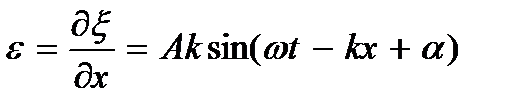
Подставляя это в выражение (9.6) и учтя, что волновое число k = = ω/v для потенциальной энергии рассматриваемой частицы будем иметь
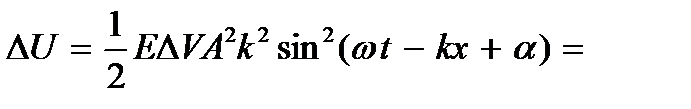
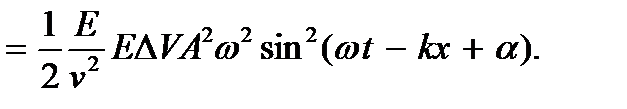
Поскольку при передаче энергии волновом процессе ΔK = ΔU, для фазовой скорости волны получим
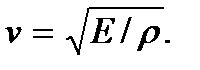 (9.7)
(9.7)
Окончательно для потенциальной энергии частицы среды будем иметь
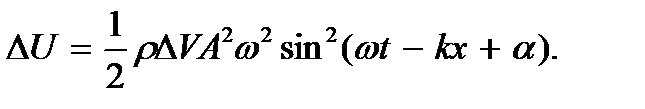
Полная энергия частицы
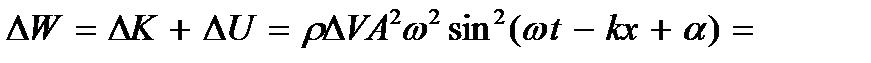
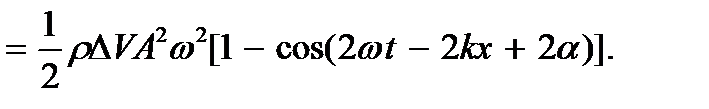
Из полученного выражения следует, что энергия волны распространяется с той же скоростью v = 2ω / 2k = ω / k, что и упругая волна, т.е. она не локализована в данном объеме, а передается посредством упругих сил от частицы к частице (эстафетный механизм распространения упругих волн). Такие волны называются бегущими волнами. Для определения энергии волны в некотором объеме V нужно проинтегрировать по этому объему. Зная энергию, определим плотность энергии:
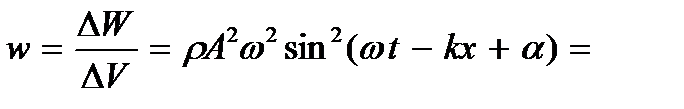
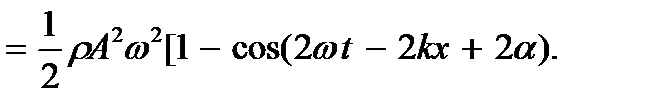
Среднее значение плотности энергии w за период найдется как
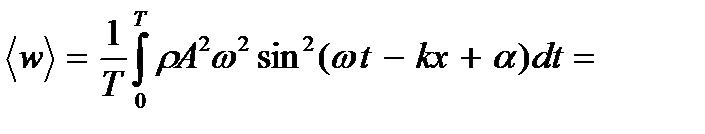
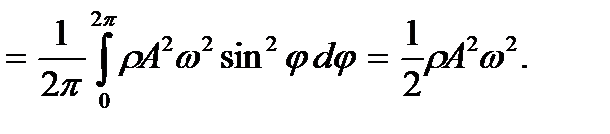 (9.8)
(9.8)
В (9.8) при переходе от первого интеграла ко второму учтено, что 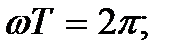 угловые скобки обозначают усреднение по времени.
угловые скобки обозначают усреднение по времени.
Энергия, переносимая волной через произвольную поверхность за единицу времени, т.е. величина 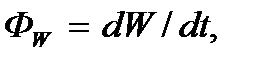 называется потоком энергии (измеряется в единицах мощности). Энергия, переносимая волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны, называется плотностью потока энергии волны, или, другими словами, поток энергии волны, проходящий через единичную площадку, перпендикулярную направлению переноса энергии. Обозначим плотность потока энергии через S. Тогда по определению
называется потоком энергии (измеряется в единицах мощности). Энергия, переносимая волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны, называется плотностью потока энергии волны, или, другими словами, поток энергии волны, проходящий через единичную площадку, перпендикулярную направлению переноса энергии. Обозначим плотность потока энергии через S. Тогда по определению 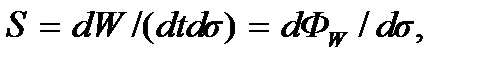 где
где 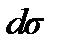 - величина площади поверхности, через которую проходит поток энергии
- величина площади поверхности, через которую проходит поток энергии 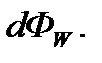 Измеряется плотность потока энергии в
Измеряется плотность потока энергии в 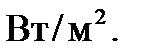
Выразим величину плотности потока энергии волны через объемную плотность энергии волнового поля. Поставим на пути волны какую-либо поверхность  (рис. 6.). Через элемент
(рис. 6.). Через элемент 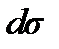 этой поверхности за время dt будет перенесена та энергия, которая заключена в прилегающем к этому элементу слое волнового поля толщиной vdt, т.е. в объеме
этой поверхности за время dt будет перенесена та энергия, которая заключена в прилегающем к этому элементу слое волнового поля толщиной vdt, т.е. в объеме 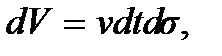 где v – скорость волны. Энергия, заключенная в этом объеме,
где v – скорость волны. Энергия, заключенная в этом объеме, 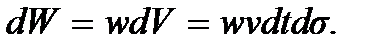 Разделив эту величину на dt, найдем поток энергии проходящий через площадку за единицу времени, а разделив затем и на
Разделив эту величину на dt, найдем поток энергии проходящий через площадку за единицу времени, а разделив затем и на 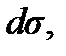 найдем плотность потока энергии волны: S = wv. Как видим, плотность потока энергии волны равна произведению объемной плотности энергии волнового поля на скорость волны. Величина w зависит от времени, поэтому и плотность потока S является функцией времени.
найдем плотность потока энергии волны: S = wv. Как видим, плотность потока энергии волны равна произведению объемной плотности энергии волнового поля на скорость волны. Величина w зависит от времени, поэтому и плотность потока S является функцией времени.
Поскольку объемная плотность энергии есть величина скалярная, а скорость – вектор, то и плотность потока энергии волны будет величиной векторной. Поэтому полученную выше формулу для плотности потока энергии волны можно записать в векторном виде S = wv. Этот вектор был введен Н.А. Умовым и называется вектором Умова. Модуль этого вектора равен плотности потока энергии волны, а направление совпадает с направлением распространения волны (так как w > 0).
Важной характеристикой волны является величина, называемая интенсивностью волны, обозначают I. Ее определяют как среднее значение за период волны от потока энергии волны:
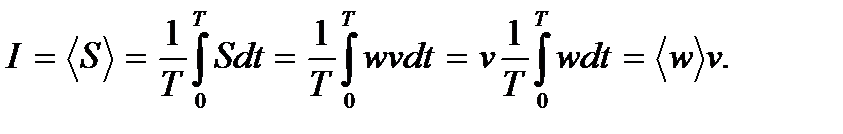
Следовательно, интенсивность волны равна произведению средней плотности энергии на скорость волны. Подставляя сюда выражение (9.8), для интенсивности волны будем иметь
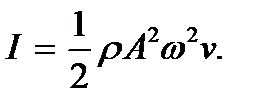
Как видим, интенсивность волны пропорциональна квадрату ее амплитуды.
Интерференция волн
Поскольку волновое уравнение (9.4) является линейным, то если 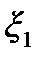 и
и 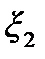 являются решениями этого уравнения, то и их сумма
являются решениями этого уравнения, то и их сумма 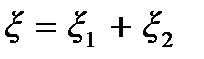 (если v1 = v2) также является решением этого уравнения. Это означает, что волны, как и колебания, можно складывать, т.е. для волн, как и для колебаний, справедлив принцип суперпозиции. В данном случае это означает, что в пространстве может распространяться неограниченное количество волн, не влияя друг на друга и не искажая друг друга.
(если v1 = v2) также является решением этого уравнения. Это означает, что волны, как и колебания, можно складывать, т.е. для волн, как и для колебаний, справедлив принцип суперпозиции. В данном случае это означает, что в пространстве может распространяться неограниченное количество волн, не влияя друг на друга и не искажая друг друга.
Распространяясь в пространстве, волны от разных источников могут накладываться друг на друга и создавать в каждой точке наложения колебание, определяемое геометрической суммой колебаний, возбуждаемых каждой из волн в отдельности. Рассмотрим для простоты случай двух гармонических сферических волн, распространяющихся от точечных источников S1 и S2 и имеющих одинаковые частоты и равные нулю начальные фазы: 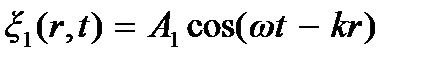 и
и 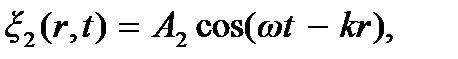 где
где 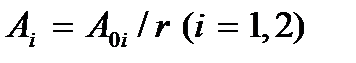 – амплитуды волн. Пусть эти волны накладываются в точке Р (рис. 9.2), находящейся на расстоянии r1 от источника S1 и на расстоянии r2 от источника S2. Будем считать, что колебания, возбуждаемые этими волнами, будут одинаково направленными. Тогда результирующее колебание
– амплитуды волн. Пусть эти волны накладываются в точке Р (рис. 9.2), находящейся на расстоянии r1 от источника S1 и на расстоянии r2 от источника S2. Будем считать, что колебания, возбуждаемые этими волнами, будут одинаково направленными. Тогда результирующее колебание
ξ = ξ1 + ξ2 = = 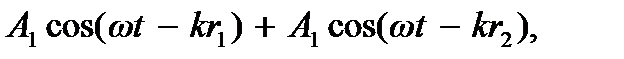
будет гармоническим колебанием с амплитудой А, определяемой выражением (5.6)
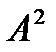 (9.5)
(9.5)
где разность фаз колебаний 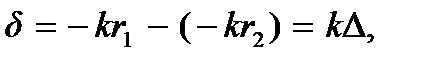
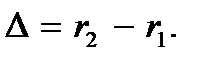 Величину ∆ называют разностью хода волн. Волновые числа
Величину ∆ называют разностью хода волн. Волновые числа 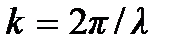 волн одинаковы, так как одинаковы частоты волн и их скорости.
волн одинаковы, так как одинаковы частоты волн и их скорости.
В этом случае разность фаз колебаний определяется разностью хода волн, и в зависимости от этой величины амплитуда колебаний будет принимать максимальные и минимальные значения. Если разность хода 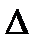 такова, что
такова, что 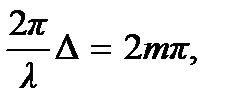 где m = = 0, 1, 2,
где m = = 0, 1, 2,
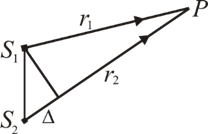 Рис. 9.2 Рис. 9.2 |
… , т.е. если разность хода 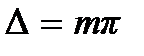 равна целому числу длин волн, амплитуда колебаний будет достигать максимального значения. В этом случае волны будут складываться в одинаковой фазе. Суперпозиция волн, фазы которых совпадают, в области их наложения дают результирующую волну, амплитуда которой равна сумме амплитуд обеих складываемых волн. При разности хода волн такой, что
равна целому числу длин волн, амплитуда колебаний будет достигать максимального значения. В этом случае волны будут складываться в одинаковой фазе. Суперпозиция волн, фазы которых совпадают, в области их наложения дают результирующую волну, амплитуда которой равна сумме амплитуд обеих складываемых волн. При разности хода волн такой, что 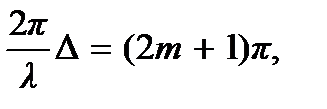 т.е. если разность хода
т.е. если разность хода 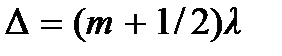 равна полуцелому числу длин волн, амплитуда колебаний достигает минимального значения. Это соответствует сложению противофазных волн. Суперпозиция волн, имеющих противоположные фазы, дают волну с амплитудой, равной разности амплитуд обеих волн. Когда обе амплитуды равны, волна затухает.
равна полуцелому числу длин волн, амплитуда колебаний достигает минимального значения. Это соответствует сложению противофазных волн. Суперпозиция волн, имеющих противоположные фазы, дают волну с амплитудой, равной разности амплитуд обеих волн. Когда обе амплитуды равны, волна затухает.
Явление устойчивого во времени перераспределения колебаний в пространстве при наложении волн друг на друга, в результате которого в одних местах колебания усиливаются, а в других ослабляются, называется интерференцией волн. Это явление возникает при сложении волн, у которых разность фаз не зависит от времени. В рассматриваем случае гармонических волн, это условие выполняется, когда частоты складываемых волн одинаковы. Только в этом случае наблюдается устойчивое во времени распределение колебаний в пространстве. Волны, способные к интерференции, называются когерентными волнами. Максимумы и минимумы амплитуды колебаний называются интерференционными максимумами и минимумами. Число m называется порядком интерференции.
Учитывая, что интенсивность волны пропорциональна квадрату амплитуды, соотношение (6.5) можно записать в виде
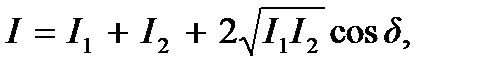 (7.6)
(7.6)
где I1 и I2 – интенсивности волн от источников S1 и S2 в точке P. Следовательно, при наложении когерентных волн происходит устойчивое во времени перераспределение интенсивности результирующей волны.
Стоячие волны
Важным случаем интерференции волн является образование стоячих волн. Стоячие волны представляют собой не распространяющиеся в пространстве гармонические колебания с различными, но постоянными для каждой точки амплитудами. Такие волны возникают при наложении двух встречных плоских волн с одинаковой частотой и амплитудой, например, при наложении друг на друга прямой и отраженной от идеального отражателя волн.
Предположим, что в положительном направлении оси X распространяется бегущая волна 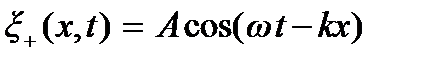 (прямая волна). При отражении ее от правой границы в точке x = l возникнет бегущая волна
(прямая волна). При отражении ее от правой границы в точке x = l возникнет бегущая волна 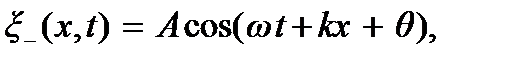 распространяющаяся вдоль отрицательного направления оси X. Слагаемое θ в фазе волны учитывает возможное изменение фазы волны при отражении. Волна
распространяющаяся вдоль отрицательного направления оси X. Слагаемое θ в фазе волны учитывает возможное изменение фазы волны при отражении. Волна 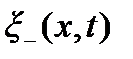 отразится от левого конца (точки
отразится от левого конца (точки 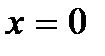 ) и будет распространяться вправо и т.д. Таким образом, на участке между точками
) и будет распространяться вправо и т.д. Таким образом, на участке между точками 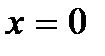 и x = l в результате многократных отражений от его границ будут распространяться в противоположных направлениях две группы волн одинаковой частоты и амплитуды. При их наложении и возникает стоячая волна.
и x = l в результате многократных отражений от его границ будут распространяться в противоположных направлениях две группы волн одинаковой частоты и амплитуды. При их наложении и возникает стоячая волна.
По принципу суперпозиции находим
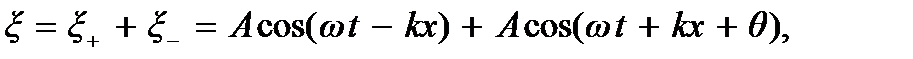
откуда
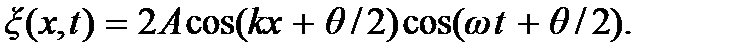 (7.7)
(7.7)
Возможны два случая: 1) изменения фазы волны при отражении не происходит; 2) при отражении волны фаза изменяется на π.
1. Если изменения фазы волны при отражении не происходит, то из выражения (6.7) получаем
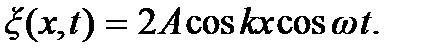 (7.8)
(7.8)
Эта функция описывает колебание с частотой ω. Величина 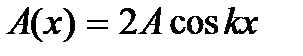 не зависит от времени и поэтому имеет постоянное значение для фиксированной точки x. Эту величину называют амплитудой стоячей волны. Следовательно, при отражении волн на границах устанавливаются колебания с амплитудой
не зависит от времени и поэтому имеет постоянное значение для фиксированной точки x. Эту величину называют амплитудой стоячей волны. Следовательно, при отражении волн на границах устанавливаются колебания с амплитудой 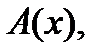 которая изменяется от точки к точке по гармоническому закону, но для данной точки является постоянной. Таким образом, в отличие от бегущих волн, для которых фаза колебаний изменяется в зависимости от координаты x, а амплитуда постоянна, в стоячих волнах амплитуда зависит от координаты колеблющейся точки, а фаза постоянна. При этом амплитуда колебаний в одних точках будет принимать максимальные (равные 2А), а в других минимальные (равные нулю) значения. Точки с максимальной амплитудой называются пучностями стоячей волны, а точки с минимальной амплитудой – узлами стоячей волны. Колебания точек в стоячей волне показаны на рис. 9.
которая изменяется от точки к точке по гармоническому закону, но для данной точки является постоянной. Таким образом, в отличие от бегущих волн, для которых фаза колебаний изменяется в зависимости от координаты x, а амплитуда постоянна, в стоячих волнах амплитуда зависит от координаты колеблющейся точки, а фаза постоянна. При этом амплитуда колебаний в одних точках будет принимать максимальные (равные 2А), а в других минимальные (равные нулю) значения. Точки с максимальной амплитудой называются пучностями стоячей волны, а точки с минимальной амплитудой – узлами стоячей волны. Колебания точек в стоячей волне показаны на рис. 9.
Координаты пучностей стоячей волны находятся из условия А(x) = 2А. Это условие сводится к условию 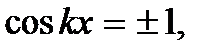 из которого получаем
из которого получаем 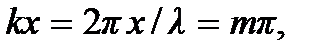 где
где 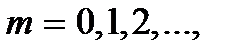 и тогда
и тогда
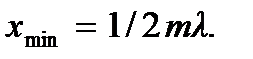 (7.9)
(7.9)
Координаты узлов находятся из условия 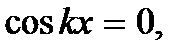 откуда
откуда 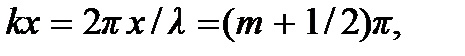 где
где 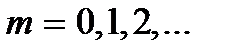 Следовательно,
Следовательно,
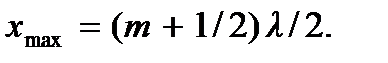 (7.10)
(7.10)
В точки пучностей бегущие встречные волны приходят в одинаковых фазах и тем самым усиливают друг друга. В точки узлов волны приходят в противофазе, и поэтому взаимно гасятся. Из формул (7.8) и (7.9) следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно 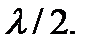 Пучности и узлы находятся друг от друга на расстоянии
Пучности и узлы находятся друг от друга на расстоянии 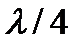 (рис. 9, а).
(рис. 9, а).

Рис. 9.
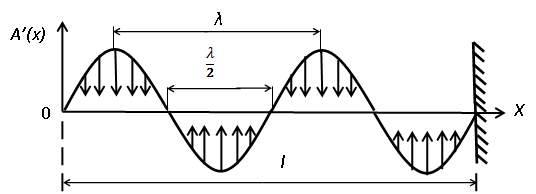
Рис. 9
Множитель 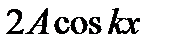 при переходе через нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от узла отличается на π, так что точки, лежащие по разные стороны от узла, колеблются в противофазе. Точки же, лежащие между соседними узлами, колеблются синфазно.
при переходе через нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от узла отличается на π, так что точки, лежащие по разные стороны от узла, колеблются в противофазе. Точки же, лежащие между соседними узлами, колеблются синфазно.
Стоячая волна не переносит энергию, так как количество энергии, переносимой падающей волной в одном направлении, равно количеству энергии, переносимой отраженной волной в противоположном направлении.
2. Если фаза волны при отражении меняется на противоположную, т.е. 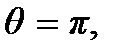 то выражение (6.7) принимает вид
то выражение (6.7) принимает вид
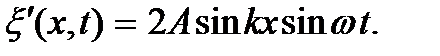 (7.11)
(7.11)
Теперь устанавливаются колебания с частотой ω и амплитудой 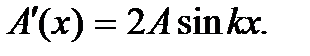 Вид такой волны показан на рис. 9, б. В этом случае, как легко убедиться, пучности и узлы стоячей волны поменяются местами: узлы займут место пучностей, и наоборот. Пучности будут иметь координаты
Вид такой волны показан на рис. 9, б. В этом случае, как легко убедиться, пучности и узлы стоячей волны поменяются местами: узлы займут место пучностей, и наоборот. Пучности будут иметь координаты 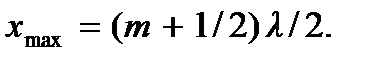 а узлы – координаты
а узлы – координаты 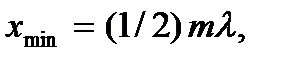
| n = 1 |
| l |
| n = 2 |
| n = 3 |
Изменение фазы волны на на π (или, как говорят, потеря полуволны) происходит на границе раздела сред, если волна отражается от более плотной среды. При отражении волны от среды менее плотной изменения фазы не происходит.
Колебания струны
Рассмотрим натянутую вдоль оси X струну длины l, закрепленную на концах (в точках x = 0 и x = l). Под струной понимают тонкую упругую гибкую нить. Гибкость струны означает, что струна не оказывает сопротивления изменению ее формы, не связанному с изменением ее длины, а силы натяжения T(x), возникающие в струне, всегда направлены по касательной к ее мгновенному профилю. Если вывести струну из положения равновесия и
затем отпустить, то струна начнет колебаться, при этом точка струны, занимающая при равновесии положение 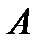 , к моменту времени t займет положение
, к моменту времени t займет положение 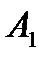 (рис. 9.3). Поскольку струна колеблется в одной плоскости, то закон ее колебаний будет задаваться одной функцией двух переменных
(рис. 9.3). Поскольку струна колеблется в одной плоскости, то закон ее колебаний будет задаваться одной функцией двух переменных 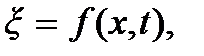 где
где 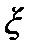 – отклонение точек струны от положения равновесия.
– отклонение точек струны от положения равновесия.
Рассмотрим участок струны, заключенный между точками 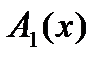 и
и 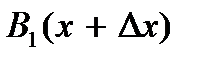 и спроецируем силы, действующие на него, на вертикальную координатную ось
и спроецируем силы, действующие на него, на вертикальную координатную ось  При малых колебаниях удлинение участков струны не происходит, поэтому по закону Гука силу натяжения T можно считать постоянной, независящей
При малых колебаниях удлинение участков струны не происходит, поэтому по закону Гука силу натяжения T можно считать постоянной, независящей
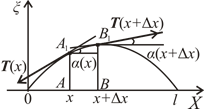 Рис. 9.3 Рис. 9.3 |
ни от времени, ни от координаты и равной 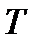 во всех точках. Эти векторы направлены по касательным к струне в соответствующих точках. Тогда проекции силы натяжения струны на ось
во всех точках. Эти векторы направлены по касательным к струне в соответствующих точках. Тогда проекции силы натяжения струны на ось 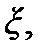 взятые в указанных точках
взятые в указанных точках 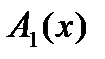 и
и 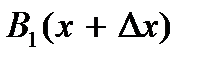 при малых углах
при малых углах 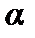 будут равны
будут равны
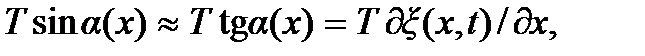
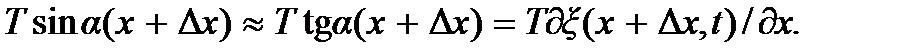
При получении этих выражений было учтено, что тангенс угла наклона касательной к кривой в какой-либо точке равен производной функции в этой точке. Разность этих проекций есть сила, приводящая в движение участок ∆x. Масса этого участка 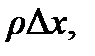 где
где 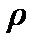 – линейная плотность струны. Тогда по второму закону динамики будем иметь
– линейная плотность струны. Тогда по второму закону динамики будем иметь
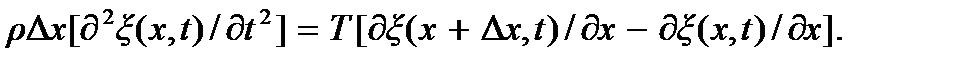
Учитывая, что при 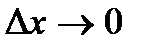
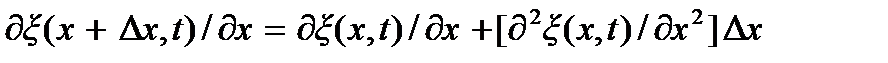
и введя обозначение 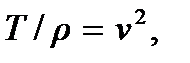 придем к уравнению
придем к уравнению
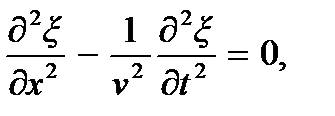
совпадающему с уравнением (7.2). Следовательно, малые свободные поперечные колебания струны представляют собой упругие изгибные волны; параметр
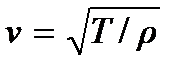 (7.12)
(7.12)
имеет смысл скорости распространения упругой волны в струне. Заметим, что скорость этих волн тем больше, чем сильнее натянута струна и чем она тоньше (в этом случае линейная плотность струны будет меньше).
Таким образом, если возбудить колебание струны, то по струне побегут упругие волны. Так как струна имеет конечную дину, то на ее концах происходит отражение волн; возникают две волны, бегущие в противоположных направлениях – прямая и обратная, которые, накладываясь друг на друга, образуют стоячую волну. Если концы струны закреплены, то там колебания отсутствуют, и тогда 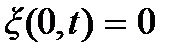 и
и 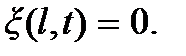 Эти равенства представляют собой граничные условия задачи о колебании струны. Непосредственной подстановкой легко убедиться, что решением волнового уравнения, удовлетворяющего условию закрепления струны в точке x = 0, т.е. первому граничному условию
Эти равенства представляют собой граничные условия задачи о колебании струны. Непосредственной подстановкой легко убедиться, что решением волнового уравнения, удовлетворяющего условию закрепления струны в точке x = 0, т.е. первому граничному условию 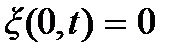 , является функция, описывающая стоячую волну
, является функция, описывающая стоячую волну
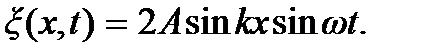 (7.13)
(7.13)
Если струна в точке x = 0 не закреплена, то в этой точке будет максимум амплитуды колебаний, и тогда
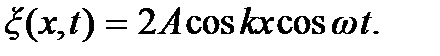
Решение вида (7.13) получается, если волна, распространяющаяся справа налево, при отражении от левого конца (x = 0) изменяет свою фазу на 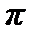 . Изменение фазы на противоположную при отражении от закрепленного конца происходит потому, что колебания любой точки струны есть результат сложения двух гармонических колебаний, вызываемых падающей и отраженной волнами. Поэтому, если конец струны закреплен, то складываемые колебания в этой точке должны погасить друг друга, т.е. они должны происходить в противофазе.
. Изменение фазы на противоположную при отражении от закрепленного конца происходит потому, что колебания любой точки струны есть результат сложения двух гармонических колебаний, вызываемых падающей и отраженной волнами. Поэтому, если конец струны закреплен, то складываемые колебания в этой точке должны погасить друг друга, т.е. они должны происходить в противофазе.
Из условия закрепления струны в точке x = l, т.е. из второго граничного условия 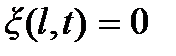 , получаем
, получаем 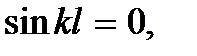 откуда
откуда 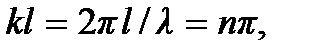 или
или 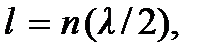 где
где 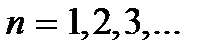 Это условие можно записать в виде
Это условие можно записать в виде 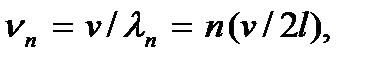 где v – скорость распространения волн в струне, или
где v – скорость распространения волн в струне, или 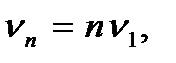 где
где 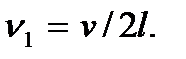 Следовательно, в струне возникают только такие колебания, половина длины волны которых укладывается на длине струны целое число раз или частоты которых являются целыми кратными некоторой частоте
Следовательно, в струне возникают только такие колебания, половина длины волны которых укладывается на длине струны целое число раз или частоты которых являются целыми кратными некоторой частоте 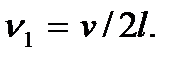
Натянутая струна представляет собой колебательную систему. Колебания струны, описываемые функциями (7.10), называют гармониками. Их называют также собственными колебаниями или модами, частоты колебаний 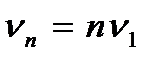 называют собственными частотами. Частота
называют собственными частотами. Частота 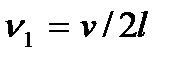 называется основной частотой. Каждой собственной частоте соответствует своя колебательная форма, или так называемая мода струны. Совокупность частот
называется основной частотой. Каждой собственной частоте соответствует своя колебательная форма, или так называемая мода струны. Совокупность частот 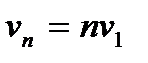 образует частотный спектр колебаний струны. Этот спектр, как видим, состоит из отдельных частот
образует частотный спектр колебаний струны. Этот спектр, как видим, состоит из отдельных частот 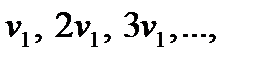 т.е. является дискретным, или линейчатым. Дискретность спектра частот является свойством всех стоячих волн. Заметим, что возникновение собственных колебаний в струне связано с выполнением определенных условий на концах струны (граничных условий). Отметим также, что колебания струны характеризуются бесконечным числом собственных частот.
т.е. является дискретным, или линейчатым. Дискретность спектра частот является свойством всех стоячих волн. Заметим, что возникновение собственных колебаний в струне связано с выполнением определенных условий на концах струны (граничных условий). Отметим также, что колебания струны характеризуются бесконечным числом собственных частот.
Таким образом, струна, возбуждаемая тем или иным способом, колеблется, имея определенный набор собственных частот (спектр).
Колеблющаяся струна издает звук, т.е. создает распространяющиеся в воздухе упругие волны. Звук, издаваемый струной, колеблющейся с минимальной частотой 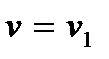 , называется основным тоном, а все другие (
, называется основным тоном, а все другие ( 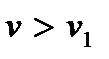 ) – обертонами.
) – обертонами.
Если на струну действует внешняя вынуждающая сила и ее частота совпадает с частотой одного из собственных колебаний струны, наступает явление резонанса.
