Рекомендации по выполнению. Корреляционно-регрессионный и статистический анализ с использованием Excel

ЛАБОРАТОРНАЯ РАБОТА № 8

Корреляционно-регрессионный и статистический анализ с использованием Excel

Цель занятия: изучить возможности табличного процессора Excel для проведения корреляционно-регрессионного и статистического анализа.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В экономике часто возникает задача подбора функциональной зависимости для двух наборов данных. В Excel введен набор функций, который позволяет решать эту задачу. Эти функции основаны на методе наименьших квадратов. Но регрессионный анализ — это не только метод наименьших квадратов. Относительно исходных данных делаются еще некоторые статистические предположения. В качестве результата выдаются не только коэффициенты функции, приближающие данные но и статистические характеристики полученных результатов. Набор подобных функций находится в категории Статистические.

Корреляция

Метод регрессионного и корреляционного анализа широко использу­ется для определения тесноты связи между показателями, не находя­щимися в функциональной зависимости. Теснота связи между изуча­емыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчис­ляется коэффициент корреляции.

Коэффициент корреляции используется для определения наличия взаи­мосвязи и ее количественной оценки двух наборов данных. Например, можно установить зависимость между величиной складского товаро­оборота и размером складской площади. Коэффициент корреляции вы­борки представляет собой ковариацию двух наборов данных, деленную на произведение их стандартных отклонений. Уравнение для коэффи­циента корреляции имеет следующий вид:

где х и у – значения изучаемых признаков;

n - количество значений х и у в выборке;

ơ_х ơ_у - средние квадратичные отклонения;

х и у – средние величины по каждому признаку;

ơ ²_ху - межгрупповая дисперсия результативного признака по фактическому.

Для характеристики изменчивости признаков используют следующие показатели: вариационный размах, среднеквадратическое отклонение и коэффициент вариации.

Вариационный размах (амплитуда колебания) — разница между макси­мальным и минимальным значениями изучаемого признака. Размах дает представление о крайних пределах вариации признаков, но не показы­вает степени изменчивости.

Среднее квадратичное отклонение (ơ) характеризует степень измен­чивости признака в абсолютных величинах. В нормальных или близких к ним вариационных рядах отклонение вправо и влево от средней (х) относятся на три сигмы (3σ). По этому показателю средней изменчиво­сти можно ориентировочно определить минимальное и максимальное значения х.

Коэффициент вариации характеризует изменчивость признака в изуча­емой совокупности в относительных величинах. Его исчисляют как процентное отношение среднего квадратичного отклонения изучаемой совокупности к средней арифметической. Изменчивость признака счи­тается незначительной, когда коэффициент вариации не более 10%, сред­ней — от 11 до 30%, высокой — свыше 30%:

Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т.е. большие значения из одного набо­ра данных связаны с большими значениями другого набора (положи­тельная корреляция) или, наоборот, малые значения одного набора свя­заны с большими значениями другого набора (отрицательная корреляция), или данные двух диапазонов никак не связаны (корреля­ция близка к нулю). Для вычисления коэффициента корреляции между двумя наборами данных используется статистическая функция

КОРРЕЛ(находится в категории Статистические). Функция КОРРЕЛ рассчитывает коэффициент корреляции между диа­пазонами или массивами ячеек.

Синтаксис функции выглядит так: КОРРЕЛ(массив1;массив2), где массив1 (fх)- — это первый интервал ячеек со значениями; массив2 (f_x) — это второй интервал ячеек со значениями.

Аргументами функции могут быть числа, имена, массивы или ссылки содержащие числа. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то та­кие значения игнорируются. Однако ячейки с нулевыми значениями учитываются.

Если массив1 и массив2 имеют различное количество точек данных (разное количество ячеек), то функция КОРРЕЛ объявляет значение ошибки.

Если массив1 и массив2 пусты или стандартное отклонение (s) их зна­чений равно нулю, то функция КОРРЕЛ указывает значение ошибки. Корреляционные связи различают:

- по количеству признаков связи: однофакторные и многофактор­ные;

- по направленности: положительные и отрицательные;

- по аналитическому выражению: прямолинейные и криволи­нейные.

Тесноту корреляционной связи определяют с помощью корреляцион­ной решетки, построенной в прямоугольных осях координат.

Если частоты распределяются ближе к диагонали, то между признака­ми обнаружена высокая связь. Размещение частот близко к диагонали, пересекающей решетку с левого нижнего в правый верхний угол, сви­детельствует о положительной направленности, а с верхнего левого в правый нижний угол — об отрицательной направленности. Дугооб­разное размещение частот в решетке характеризует криволинейную связь и беспорядочное отсутствие связи. В процессе выбора модели урав­нения учитывают также характер динамического ряда. Уравнение пря­мой используется, когда на протяжении изучаемого периода сохраня­ется более или менее стабильный абсолютный прирост явления, При зигзагообразном возрастающем изменении динамического ряда без ста­бильного его роста и снижении применяют уравнение параболы. При отрицательной направленности и изменении динамических рядов по зиг­загообразной снижающей, а затем повышающей кривой без стабильно­го их снижения и роста используют уравнение гиперболы или кривой показательной функции.

Для измерения тесноты связи между результатом и признаками используются коэффициенты линейной и множественной корреляции, а также коэффициент регрессии.

Коэффициент линейной корреляции — показатель, отображающий на­правление и тесноту связи между признаками при прямолинейных (или близких к ним) взаимозависимостях. Он колеблется в пределах от 0 до ±1. Знак «+» означает прямую, а знак «-» — обратную связь. Значе­ния коэффициента линейной корреляции и теснота связи между при­знаками указаны в табл. 1.1.

Таблица 1.1

Значение коэффициента линейной корреляции	Теснота связи
	±0,15	Связь отсутствует
от±	0,1 6 до ±0,20	Плохая связь
от±	0,21 до ±0,30	Слабая связь
от ±0,31 до ±0,40	Умеренная связь
от±	0,41 до ±0,60	Средняя связь
от±	0,61 до ±0,80	Высокая связь
от±	0,81 до ±0,90	Очень высокая	связь
от±	0,91 до ± 1,0	Полная связь

Теснота связи двух или более признаков выражается коэффициентом множественной корреляции (совокупной). Коэффициент множественной корреляции — число всегда положитель­ное и изменяется от 0 до 1. Для его исчисления предварительно вычис­ляют частные коэффициенты корреляции

Регрессия

Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия значений одной или более зависимых переменных на отдельную зависимую переменную Например, на объем оптово-складского товарооборота влияют складская площадь, величина товарных запасов и другие факторы. Регрессия пропорционально распределяет меру качества по этим факторам.

Линейное уравнение регрессии имеет следующий вид:

Y=a + bx, (

где а - независимая переменная;

Ь - значение коэффициента при переменной;

х - значение переменной.

Коэффициент регрессии (R) — величина, которая характеризует, на­сколько изменяется изучаемый признак исследуемого явления (сово­купности) при изменении корреляционного признака на определенную величину. Коэффициент регрессии исчисляется по формулам:

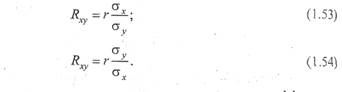
Коэффициент регрессии имеет два значения и включает коэффициент корреляции (r) и ơ_х ơ_у - средние квадратичные отклонения по обоим призна­кам Он может быть положительным и отрицательным в зави­симости от значения коэффициента корреляции.

Статистический анализ

В Excel имеется набор инструментов для анализа данных, называемый «пакет анализа данных», который может быть использован для реше­ния сложных статистических задач. Для использования одного из этих инструментов необходимо указать входные данные и выбрать парамет­ры, анализ которых будет проведен с помощью статистической макро­функции, и результаты будут представлены в выходном диапазоне. Некоторые инструменты позволяют представить результаты в графи­ческом виде.

После выполнения команды СЕРВИС —Анализ данных из меню на эк­ране появляется окно диалога, в котором перечислены инструменты статистического анализа данных.

Инструмент Генерация случайных чисел позволяет строить последо­вательности случайных чисел, распределенных в соответствии с нормальным распределением, распределением Бернулли, Пуассона, равномерным, биномиальным и другими видами распределений.

Инструмент Описательная статистика предлагает таблицу основных статистиче­ских характеристик для заданного множества исходных данных: сред­нее, стандартная ошибка, медиана, мода, стандартное отклонение, дис­персия и т.д. Для вывода таблицы должен быть включен флажок Итоговая статистика, можно также проверить распределение на «нор­мальность».

Инструмент Гистограмма строит диаграмму, в которой для исход­ного множества значений определяется количество значений (час­тот), попадающих в интервалы разбиения — карманы. При постро­ении гистограммы следует ввести: место расположения исходных данных, границы интервалов разбиения и верхнюю левую ячейку выходного диапазона. Если интервал карманов пуст, создаются рав­ные интервалы разбиения в количестве, равном квадратному корню из числа входных значений. Для получения графика необходимо уста­новить флажок Вывод графика, иначе будет выведена только таб­лица с указанием карманов и частот для каждого из них. Флажок Парето используется для сортировки выходных, значений в порядке убывания частот, флажок Интегральный процент — для включе­ния в таблицу накопленных частот в процентах для интервала гис­тограммы.

Инструмент Выборка извлекает из множества значений заданное их подмножество либо случайным образом, либо выбирая каждое н-е зна­чение.

Инструмент Скользящее среднее позволяет выполнить анализ тен­денции путем сглаживания колебаний измерений за некоторый период времени.

ПРАКТИКУМ

Задание 1. Рассчитать коэффициент корреляции, характеризующий тесноту связи между величиной оптово-складского това­рооборота и размером складской площади фирмы. Значе­ния элементов X (складская площадь) и Y (оптово-складской товарооборот) указаны в табл. 1.15.

Рекомендации по выполнению

1. Создайте таблицу с исходными данными.

Исходные данные

2. Рассчитайте коэффициент корреляции по следующей формуле:
=КОРРЕЛ(В2:В5;С2:С5). Функция КОРРЕЛ может быть вызвана
с помощью Мастера функций из категории Статистические.

3. В диалоговом окне функции указываются массивы Складской
площади и Оптово-складского товарооборота.

4. В итоге должен быть получен результат КОРРЕЛ =0,353990796.

Задание 2.На основе данных предыдущего задания выполнить рег­рессионный анализ.