Общая схема исследования функций. Исследование графиков

План исследования функции и построение графика

Исследование функции удобно проводить по следующему плану.

1. Область определения функции.

2. Точки пересечения графика функции с осями координат.

3. Четность, нечетность функции.

4. Исследование функции на непрерывность. Вертикальные асимптоты.

5. Невертикальные асимптоты.

6. Интервалы монотонности. Экстремумы.

7. Интервалы выпуклости, вогнутости. Точки перегиба.

8. Дополнительные точки, 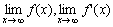(по мере необходимости).

9. Построение графика.

Подчеркнем, что пункт 8 не является необходимым. его выполняют, если необходимо уточнить график.

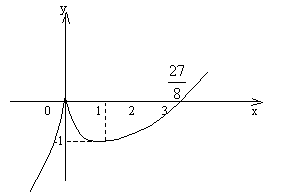
Пример 1. Исследовать функцию 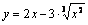и построить ее график.

1. Область определения ( ).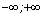

2. Пусть х=0, тогда у=0. Пусть у=0, тогда 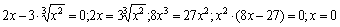и . И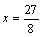так, (0;0) и 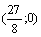– точки пересечение графика с осями координат.

3. у(-х) = 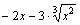– функция не является ни четной, ни нечетной.

4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.

5. Невертикальные асимптоты

Найдем k и b, если они существуют. 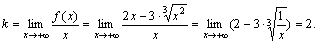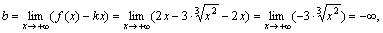поэтому при 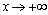невертикальной асимптоты не существует. Аналогично можно показать, что и при 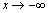невертикальных асимптот не существует.

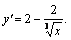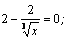
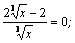
6. Вычислим Найдем критические точки: 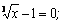х =1– критическая точка. Кроме того, y' не существует при х = 0 – тоже критическая точка. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.

Таким образом, на интервалах (- 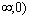и (1;+ 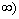функция возрастает, на интервале (0;1) убывает.

у_max = f(0)= 0, y_min = f(1)= -1.

7. Вычислим

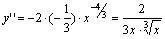
у'' не обращается в нуль ни при каком значении х и у'' не существует при х=0. х=0 – критическая точка второго порядка. Нанесем критическую точку на числовую прямую и определим знаки второй производной в образовавшихся интервалах.

Таким образом, на интервалах ( 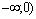и 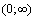график функции вогнутый, точек перегиба нет.

8. Заметим, что 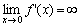, то есть в точке (0;0) график имеет вертикальную касательную.

20. Определение неопределённого интеграла и его свойства.

Дадим строгое математическое определение понятия неопределенного интеграла.

Выражение вида 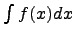называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом 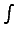всегда присутствует dx.

Определение. Неопределенным интегралом 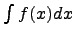называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. 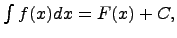или 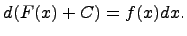Функцию 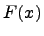называют первообразной функции 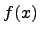. Первообразная функции 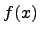определяется с точностью до постоянной величины.

Напомним, что 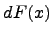-дифференциал функции 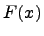и определяется следующим образом:

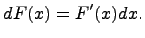
Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.

Например, известно, что 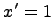, тогда получается, что 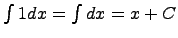, здесь 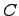- произвольная постоянная.

Основные свойства неопределённого интеграла

Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то

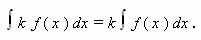
Короче: постоянную можно выносить за знак интеграла.

Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то

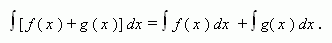
Короче: интеграл суммы равен сумме интегралов.

Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:

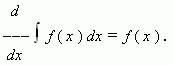
Короче: производная от интеграла равна подынтегральной функции.

Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:

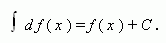
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования

Таблица интегралов.

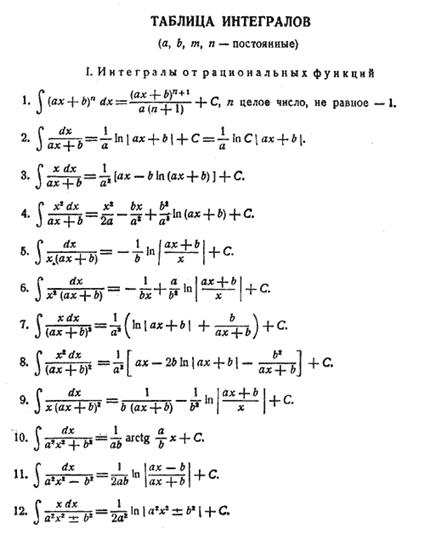
22. Формулы интегрирования по частям и её вывод.

Пусть надо вычислить интеграл вида

∫ U(x) · v(x) dx ,

где v(x) имеет очевидную первообразную V(x).

Тогда

∫ U(x) · v(x) dx = ∫ U(x) · V'(x) dx = ∫ U(x) dV(x) .

Такого рода преобразование называется подведением под знак дифференциала, поскольку функция v(x) исчезает в интегрируемом выражении и появляется под знаком дифференциала в виде своей первообразной V(x).

Если функция U(x) выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то

∫ U(x) dV(x) = ∫ w(V(x)) dV(x) = ∫ w(t) dt ,

где t = V(x). Таким образом отыскание исходного интеграла сводится к отысканию интеграла

∫ w(t) dt

В нем функция t = V(x) выступает как независимая переменная, т.е. произошла замена переменной.

Если функция U(x) не выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то может оказаться полезным преобразование, называемое интегрированием по частям. Оно определяется следующей теоремой.

Теорема 1. Пусть функции U(x) и V(x) дифференцируемы на некотором интервале и на этом интервале существует интеграл ∫ V(x)U '(x) dx .

Тогда существует интеграл ∫ U(x)V '(x) dx и справедлива формула

∫ U(x)V '(x) dx = U(x)V(x) − ∫ U '(x)V(x) dx.

(1)

Доказательство следует из формулы дифференцирования произведения. Оно приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 168.

Замечание 1. Очевидно, что в формуле интегрирования по частям оператор дифференцирования, обозначенный штрихом, перемещается с V на U. Этим обусловлена важная роль формулы при доказательстве самосопряженности линейных дифференциальных операторов.

Замечание 2. Формулу интегрирования по частям удобно применять также в виде

∫ U(x) · v(x) dx = U(x) · V(x) − ∫ u(x) · V(x) dx,

(2)

где функция v(x) имеет очевидную первообразную V(x) , а U(x) — дифференцируемая функция, причем ее производная u(x) = U'(x) является более простой функцией, чем она сама.

Замечание 3. Формулу интегрирования по частям (1) можно представить в виде в виде

∫ U(x) dV(x) = U(x)V(x) − ∫ V(x) dU(x) .

(3)

Метод интегрирования по частям применяется в следующих случаях:

1. Подынтегральное выражение содержит в качестве множителя одну из функций ln x , arcsin x , arccos x , arctg x . Если применить формулу (2), полагая в ней U(x) равной одной из этих функций, то подынтегральное выражение Vxu(x) может оказаться проще исходного.

2. Подынтегральное выражение имеет вид: Pn(x) eαx , Pn(x)sinαx или P(x)cosαx , где Pn(x) — многочлен степени n .

Интегралы от таких функций вычисляются n –кратным применения формулы интегрирования по частям (1), причем в качестве U(x) каждый раз следует брать многочлен. После каждого интегрирования по частям степень многочлена понижается на единицу.

3. Подынтегральное выражение имеет вид

eαx · cosβx, eαx · sinβx, sin(lnx), cos(lnx).

После двукратного интегрирования по частям получается линейное алгебраическое уравнение относительно исходного интеграла.

4. После подведения под знак дифференциала получился интеграл ∫ U(x) dV(x) , в котором функция U(x) не выражается через V(x), но функция V(x) выражается через U(x). Тогда можно применить формулу интегрирования по частям